
Classe terza - percorso iniziale
Nella classe terza che ha partecipato al laboratorio l'avvio al calcolo differenziale è stato preceduto da alcune attività volte a introdurre il concetto di funzione. La classe, infatti, proveniva da un biennio di Lceo Scientifico con insegnamento impostato "tradizionalmente", in cui gli alunni non avevano ancora affrontato questo concetto.
Per l'introduzione del concetto di funzione, anche in relazione allo sviluppo futuro,
in cui erano previsti degli intrecci con la fisica,
si è pensato di partire da alcuni esempi di modellizzazione matematica di fenomeni fisici
che comportassero l'impiego di funzioni elementari, esprimibili attraverso la composizione delle
"4 operazioni".
Come primo contesto di è pensato allo studio della convergenza di una lente,
e in particolare alla relazione tra posizione di un oggetto luminoso e posizione della sua immagine
(nitida) proiettata da una lente convergente su uno schermo. La scelta è stata motivata anche
dall'idea di giocare sul termine "immagine dell'oggetto" per avviare il concetto di funzione,
oltre che dalla possibilità di esplorare dinamicamente la relazione input-output
che presenta questo fenomeno.
Come contesto successivo si è preso in esame lo studio dell'allungamento di una molla,
e, in particolare, la determinazione del coefficiente di elasticità. La scelta è stata motivata con l'idea di
mettere meglio a fuoco i diversi ruoli delle variabili (variabili assunte come "di input", come "di output", come "parametri")
e il concetto di pendenza, oltre che altri aspetti delle attività di modellizzazione.
Immagine di un oggetto proiettata da una lente
Esplorazione iniziale
L'attività si è avviata con l'osservazione di fenomeni quali: il posizionamento di una lente
in modo da veder proiettata nitidamente, su fogli posti sui banchi, l'immagine della lampada della classe
e, poi, il posizionamento di lente, schermo, oggetto nel caso di altri oggetti luminosi.
In questa fase esplorativa si è osservato che la "distanza dell'oggetto" e la "distanza dell'immagine" (sottinteso "dallo schermo")
variano una al variare dell'altra, che se l'oggetto è troppo vicino spostando lo schermo non se ne riesce a trovare un'immagine nitida,
che all'aumentare della distanza dell'oggetto diminuiscono le dimensioni dell'immagine e diminuisce anche la distanza
dell'immagine, che occorre allineare opportunamente schermo, lente ed oggetto per fare dei confronti significativi, ...
Messi a punto gli ingredienti per progettare un'attività di osservazione più sistematica, volta ad esplorare
meglio la relazione quantitativa tra alcune variabili (e, in particolare, tra le due distanze dallo schermo di oggetto ed immagine,
fissando altre grandezze come "parametri"),
per problemi organizzativi e di tempo, si è preferito procedere, invece che con una
esperienza diretta di laboratorio di fisica, con lo studio del fenomeno mediante una simulazione al calcolatore,
predisposta dal docente di classe mediante il programma Interactive Physics.
Esplorazione con Interactive Physics
Le due immagini che seguono illustrano le due attività di esplorazione e raccolta di informazioni che si sono
svolte:
 |
 |
CLICCA per avere un'idea (su una applet) di come si opera con il mouse per realizzare la simulazione
Analisi dei dati (e riflessione sui grafici) ottenuti con la simulazione impiegando software matematico
| I punti "sperimentali" raccolti dal programma Interactive Physics e rappresentati con altro software (un foglio elettronico - ma si potrebbe usare anche altro software): analisi del grafico, riflessione sul significato "fisico" degli asintoti verticali (i fuochi, le immagini virtuali, ...), ... |
 |
| L'idea che tra le due distanze ci sia una specie di inversa proporzionalità e i tentativi di esplorare matematicamente la relazione tra esse: alcune trasformazioni dei dati, realizzate numericamente (← vedi) e graficamente: |
 |
| Alla ricerca delle formule e il confronto (per sovrapposizione grafica) con i dati "sperimentali" |
 fx fx |
La sistemazione "teorica" (fisica)
| La legge dei punti coniugati, la costruzione "geometrica" dell'immagine, ... |  f f |
Allungamento di una molla
|
Gli alunni hanno effettuato la "taratura" di diverse molle in laboratorio di fisica.
Poi è stato posto loro il problema di come individuare il valore della costante di elasticità.
Hanno svolto questa seconda attività in aula computer.
Gli alunni non avevano determinato le precisioni delle misure, per cui hanno
rappresentato le coppie di dati rilevate sperimentalmente con dei punti, non con
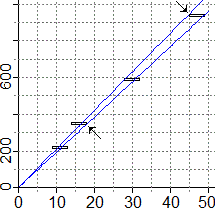
dei rettangolini. Non avevano, quindi, la possibilità di procedere nel modo raffigurato a lato (trovare
come deve essere inclinata una retta passante per l'origine in modo da passare per tutti i rettangolini,
il che avrebbe permesso di individuare un intervallo di indeterminazione per la costante di elasticità). Il docente ha, allora avviato e guidato una discussione che, gradualmente (e aprendo una breve "parentesi" di approfondimento sulle funzioni polinomiali di secondo grado), dall'idea di prendere ad occhio la retta che "passa più vicino" all'insieme dei punti sperimentali, ha portato all'idea del metodo dei minimi quadrati "con vincolo", facilmente affrontabile mediante lo studio dell'andamento di una parabola. Ecco una traccia (a livello "adulto", fatta su generici punti - in classe è stata fatta su dati sperimentali) della discussione finale: |
 |
||
| |||
Questo metodo per la ricerca della retta ottimale ha condotto anche a riflessioni sullo studio della pendenza della parabola, che sono state poi approfondite nella successiva attività di avvio al calcolo differenziale.