LOGICA MATEMATICA - 2° modulo - Parte "Algoritmi" - Traccia
1. INTRODUZIONE
Il problema della definizione dei concetti matematici si pone in modo nuovo a partire
dal XIX secolo:
da una parte in relazione alla esigenza di dare una formulazione "matematica" di
nozioni già trattate matematicamente, ma sotto l'ipoteca del significato
intuitivo (funzione, continuità, ..., insieme, ...), col quale via via sono emersi conflitti (es.: le funzioni continue intese come quelle con grafico descrivibile come linea tracciata da una penna o traiettoria di un oggetto e l'esistenza di funzioni continue con punti interni al dominio in cui non esistono derivata da destra né da sinistra; insiemi definiti come "l'insieme degli x tali che ..." il cui impiego dà luogo a contraddizioni; …).
matematizzare nuovi settori
di indagine che richiedono come premessa la definizione di nuovi oggetti
matematici (dai concetti dell'algebra astratta
gruppo, ... alla logica matematica).
La matematizzazione del concetto di algoritmo (procedimento
di calcolo) è un esempio "misto": è un concetto usato intuitivamente
sin dalla antichità, ma solo all'inizio del XX secolo viene messa
a fuoco l'esigenza di formalizzarlo, in relazione a vari aspetti.
Nel periodo di "crisi" legato alle difficoltà incontrate
quando si incomincia ad affrontare il problema di dare una organizzazione
autonoma alla matematica (problema che si è posto in seguito alla
estensione delle applicazioni e dello sviluppo interno della matematica),
per esempio alle difficoltà nei primi tentativi di formalizzare
il concetto di insieme, si precisa la distinzione tra diversi modi di concepire
la matematica; in particolare, in contrapposizione ad atteggiamenti "platonisti"
(matematica come scienza di verità o oggetti ad essa preesistenti),
si sviluppano atteggiamenti più "costruttivi":
quello "formalista" (oggetti
matematici costruiti dall'uomo, la cui organizzazione in sistemi non conraddittori
ne garantirebbe l'utilizzo: il portavoce più rappresentativo è
Hilbert; è lo sviluppo di questo indirizzo che ha condotto alla
moderna concezione della logica matematica e al concetto di sistema formale)
e quello "intuizionista",
o "costruttivista" in senso stretto (gli oggetti matematici sono costruiti,
a partire da oggetti matematici direttamente intuiti
come i numeri naturali , mediante procedimenti
di costruzione mentale che trovano nella intuizione il loro fondamento).
Questi due approcci, per diversi motivi, pongono al centro
l'idea di algortimo:
per quanto riguarda il formalismo,
nello sviluppo dei primi sistemi formali si richiede, più o meno
esplicitamente, che ci siano dei procedimenti per verificare la correttezza sintattica delle
formule, che le regole di derivazione (chiamate anche regole di inferenza) siano "meccaniche",
... in modo, ad es., da poter controllare in modo oggettivo se una dimostrazione è corretta o no (siamo negli anni '20: il primo manuale moderno di logica è
ad opera di Hilbert e Ackermann nel 1928);
l'intuizionismo alle dimostrazioni
esistenziali per assurdo, al concetto di funzione come insieme di coppie,
... tende a sostituire procedimenti per individuare una soluzione, procedimenti
per generare output a partire dagli input, ....
Anche in ambiti fondazionali più specifici emerge
l'esigenza di chiarire il concetto di algoritmo: nei primi tentativi di
definire il concetto di casualità (1919, von Mises) si incappa nel
problema di precisare (per contrasto) quali siano i procedimenti meccanici.
Questi sono i principali contesti in cui si usa e sviluppa
in modo nuovo e più generale il concetto di algortimo (già
Leibiniz, nel XVII sec., aveva introdotto l'idea di interpretare come algoritmi
le dimostrazioni). Il fattore scatenante è, però, più
specificamente, la necessità di dare alcune risposte ad alcuni problemi
di risolviblità algortimica (esiste un algortimo per calcolare la
soluzione di un certo problema?), sorti sia nell'ambito della teoria dei
numeri che in quello della nascente logica matematica (decidere se una
formula è un teorema o no, ...). Per stabilire delle risposte negative
(non esiste alcun algortimo che ...) occorre aver definito che cosa è
un algortimo.
2. CHE COS'E` UN ALGORITMO? - LA FORMALIZZAZIONE DI TURING-POST
Esercizio. Fate una rassegna dei vari modi in cui, nel corso degli
studi, avete descritto/definito algoritmi. Provate a caratterizzare a parole il concetto di algortimo. (commento).
Vi sono sostanzialmente due approcci con cui è affrontabile
il problema di definire quali sono i procedimenti calcolabili:
cercare di definire direttamente
la classe delle funzioni calcolabili,
cercare di formalizzare matematicamente
il concetto di calcolatore.
Vediamo, prima, questo secondo approccio, per noi forse
più facile da concepire, ma che non era tale intorno al 1930, quando
è stato delineato, decenni prima che nascessero i primi computer.
# Analisi da parte di Turing (intorno al 1936 -
vedi) del
concetto di algortimo (analisi di procedimenti computazionali svolti dall'uomo)
e individuazione degli aspetti essenziali (non è necessaria la bidimensionalità
del foglio, basta leggere/scrivere un simbolo per volta, ...) mediante
un opportuno modello (nastro suddiviso in celle potenzialmente illimitato;
quantità finita di simboli; un simbolo per cella; una "testina" di lettura/scrittura che può osservare - operare una scansione di - una
cella per volta, può scrivervi un simbolo e spostarsi a sinistra o a destra di una cella per volta)
# Inizialmente vedremo il modello di Turing-Post
(programmi o calcolatori/calcolatrici,
nel senso di macchine programmate di
Turing-Post), una formulazione intermedia tra quella messa a punto da Turing
(che vedremo dopo) e quella messa a punto indipendentemente (negli stessi
anni) da Emil Post (vedi: Davis, M.: 1978, 'What is a Computation?', in Steen, L.A. (ed.) Mathematics today, Springer, New York).
#

Simboli sul nastro: solo 0 e 1
Programma (o calcolatore, macchina, ...): lista di istruzioni dei tipi seguenti (la semantica è descritta tra parentesi, a cui nei primi 4 casi va aggiunto "e passa alla istruzione successiva"):
PRINT 0 (scrivi 0 nella cella su cui sei posizionato)
PRINT 1 (scrivi 1 ...)
GO LEFT (spostati nella cella immediatamente a sinsitra)
GO RIGHT (spostati ... destra)
GO TO STEP N IF 1 IS SCANNED (se sei su un
1 vai alla istruzione n-esima)
GO TO STEP N IF 0 IS SCANNED (se sei su uno
0 ...)
STOP (fermati)
Convenzione su input e output:
• la testina di lettura è inizialmente posizionata all'inizio della stringa
di input (massima porzione del nastro nella sua configurazione iniziale
che ha "1" come primo e ultimo carattere); • il programma termina quando arriva alla istruzione STOP o
quando ha eseguito l'ultima istruzione o dovrebbe passare a un'istruzione che non è nell'elenco.
| Esempio. Il programma a lato (dove i numeri delle
istruzioni sono stati aggiunti per facilitare la lettura, ma non fanno
parte del programma) è un programma che se la stringa di input è
"11" (o una qualunque altra stringa costituita non da un solo "1") si ferma,
mentre se la stringa di input è "1" continua ad spostare la testina
di lettura a destra, "ciclando" sulle prime due istruzioni. Volendo, potremmo non mettere STOP. |
1 go right
2 go to step 1 if 0 is scanned
3 stop |
# Notazioni:
P(v) per "il programma P con input v si arresta"
per "il programma P con input v si arresta"
P(v)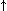 per "il programma P con input v non si
arresta"
per "il programma P con input v non si
arresta"
P(v)  w per "il programma P con input
v si arresta e ha come output w" (stringa di output:
massima porzione del nastro nella sua configurazione finale che ha "1"
come primo e ultimo carattere)
w per "il programma P con input
v si arresta e ha come output w" (stringa di output:
massima porzione del nastro nella sua configurazione finale che ha "1"
come primo e ultimo carattere)
'n' per la stringa costituita da n+1 "1"
# Rappresentazione delle funzioni a input
e output numerici (numeri naturali):
Sia F una funzione a n input e 1
output in IN e P un programma di Turing. P calcola
F se per ogni i1, ..., in  IN:
IN:
P('i1' 0 'i2' 0 ... 0 'in') |
sse |
F(i1, ...,in) è definito e, in tal caso,
P('i1' 0 'i2' 0 ... 0 'in')  'F(i1, ...,in)'
'F(i1, ...,in)' |
[in modo analogo si possono rappresentare, evidentemente, anche le funzioni
a più output numerici]
Quindi il programma dell'esempio precedente calcola la funzione a 1
input e 1 output che a n positivo associa n stesso e che
non è definita in 0: P(1...1)  1...1,
P(1)
1...1,
P(1)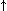 .
.
Esercizio. Come modificare il programma in modo che calcoli la funzione predecessore (definita solo per input positivi)? (risposta).
# Altri esempi di programmi di Turing-Post.
| Addizionatore. Idea: tolgo due "1" e trasformo in "1" lo "0" di separazione; se c'è un solo "1" prima di "0" mi limito a togliere questo "1": "111011", cioè (2,1), viene trasformato in "1111", cioè 3. |
1 print 0
2 go right
3 go to step 8 if 0 is scanned
4 print 0
5 go right
6 go to step 5 if 1 is scanned
7 print 1
8 stop |
| Esempio: 2+5 |
input: 1110111111
0000000000000000000011101111110000000000000000
p 0 0000000000000000000001101111110000000000000000
go R 0000000000000000000001101111110000000000000000
p 0 0000000000000000000000101111110000000000000000
go R 0000000000000000000000101111110000000000000000
go R 0000000000000000000000101111110000000000000000
p 1 0000000000000000000000111111110000000000000000
stop 0000000000000000000000111111110000000000000000
output: 11111111
|
|
1 print 0
2 go left
3 go to step 2 if 1 is scanned
4 print 1
5 go right
6 go to step 5 if 1 is scanned
7 print 1
8 go right
9 go to step 1 if 1 is scanned
10 stop |
Duplicatore (duplica stringhe di 1, ovvero a N associa 2N+1). Idea: man mano cancello un "1", ne aggiungo "1"
a sinistra e lo riscrivo, poi mi sposto a destra e faccio lo stesso con
un nuovo "1". |
# Tesi di Church (e Turing): non è possibile
trovare una funzione intuitivamente calcolabile che con sia calcolabile
con un programma di Turing-Post. È una tesi "filosofica", extramatematica,
che potremmo esprimere dicendo: il concetto matematico di programma di
Turing-Post è una formalizzazione soddisafacente del concetto intuitivo
di algoritmo. Questa considerazione era avvalorata dal fatto che tutti
gli algortimi messi a punto nell'ambito della matematica risultavano essere
rappresentabili mediante tali programmi, e dal fatto che altre formalizzazioni
messe a punto più o meno negli stessi anni sono risultate essere
equivalenti a questa. Come vedremo, ci sono in realtà funzioni calcolabili
secondo questa accezione che non sono "praticamente" calcolabili (più
che per essere troppo restrittiva, la tesi può suscitare dubbi per
il fatto che, come vedremo, questa nozione di calcolabilità include
funzioni che non sono "praticamente" calcolabili, cioè calcolabili
in tempi "umani").
3. MACCHINE A REGISTRI - Linguaggio MR [Proposta più
recente]
| Istruzioni: |
Ri = Ri + 1 Ri =
Ri 1 Ri = 0 IF Ri=
0 THEN n (i, n naturali) 1 Ri = 0 IF Ri=
0 THEN n (i, n naturali) |
| Programma: |
sequenza finita di istruzioni. |
| Semantica: |
aggiungi 1 pallina al contenitore i-esimo e passa all'istruzione successiva (qualora
questa non esista arresta l'esecuzione); togli 1 pallina, se possibile,
dal contenitore i-esimo e passa all'istruzione successiva (qualora
...); svuota il contenitore i-esimo e passa all'istruzione successiva (qualora ...); se il contenitore
i-esimo è vuoto, vai all'i-struzione n-esima del programma (qualora
questa non esista arresta l'esecuzione) altrimenti passa all'istruzione successiva (qualora ...). |
Un programma P in MR calcola F a n input e 1 output in IN se:
mettendo in R1 i1 palline, ..., in Rn
in palline (cioè prendendo R1,...,Rn
come registri di input), P si arresta sse F(i1, ..., in)
è definito e, in tal caso, in R0 (registro di output)
vi sono F(i1, ..., in) palline.
| ESEMPI |
|
Successore (sposto le palline da R1 in R0 e ne aggiungo 1) | Addizione |
IF R1 = 0 THEN 5
R1 = R1 1
R0 = R0+1
IF R2 = 0 THEN 1 (funge da GOTO 1)
R0 = R0+1 1
R0 = R0+1
IF R2 = 0 THEN 1 (funge da GOTO 1)
R0 = R0+1 |
IF R2 = 0 THEN 5
R2 = R2 1
R0 = R0+1
IF R3 = 0 THEN 1
IF R1 = 0 THEN 9
R1 = R1 1
R0 = R0+1
IF R3 = 0 THEN 1
IF R1 = 0 THEN 9
R1 = R1 1
R0 = R0+1
IF R3 = 0 THEN 5 1
R0 = R0+1
IF R3 = 0 THEN 5 |
Il seguente linguaggio L è una estensione conservativa
di MR (nel senso che ogni programma realizzabile con L è estensionalmente
equivalente a un programma realizzabile con MR: a parità di input
fornisce gli stessi output; sul concetto di estensionalità ritorneremo
più avanti):
| Istruzioni: quelle di MR più: |
(A) GOTO n (B) END
(C) Ri =n (D) Ri = Rj
(E) Ri = Rj+Rk
(F) Ri = Rj*Rk
(G) Ri = Rj Rk (H) IF Ri = Rj
THEN n Rk (H) IF Ri = Rj
THEN n |
Per la dimostrazione basta esibire come tradurre in MR un programma di
L.
Procedo seguendo l'ordine con cui le istruzioni compaiono nel programma.
Indico con max l'indice massimo tra i registri che compaiono nel
programma [e con LEN la lunghezza, ossia, in questo caso, il numero di linee, del programma].
| A) |
m-1) ...
m) GOTO n
m+1) ... |
 * * |
m-1) ...
m) Rmax+1= 0
m+1) IF Rmax+1= 0 THEN n
m+2) ... (ex n+1-esima istruzione) |
| B) |
m-1) ...
m) END
m+1) ... |
 |
m-1) ...
m) GOTO 0 [o GOTO LEN+1]
m+1) ... |
| C) |
m-1) ...
m) Ri =n
m+1) ... |
 |
m-1) ...
m) Ri = 0
m+1) Ri =Ri+1
...
m+n) Ri =Ri+1
m+n+1) ... (ex m+1-esima istruzione) |
| D) |
m-1) ...
m) Ri =Rj
m+1) ... |
 * * |
m-1) ...
m) Ri = 0
m+1) ... m+1) IF Rj
= 0 THEN m+6
m+2) Rj = Rj 1 1
m+3) Rmax+1=Rmax+1+1
m+4) Ri =Ri+1
m+5) GOTO m+1
m+6) IF Rmax+1= 0 THEN m+10
m+7) Rmax+1=Rmax+1 1 1
m+8) Rj =Rj+1
m+9) GOTO m+6
m+10) ... (ex m+1-esima istruzione) |
| E) |
m-1) ...
m) Ri =Rj+Rk
m+1) ... |
 * * |
m-1) ...
m) Ri = Rj
m+1) Rmax+1=Rk
m+2) IF Rmax+1 = 0 THEN m+6
m+3) Rmax+1=Rmax+1 1 1
m+4) Ri =Ri+1
m+5) GOTO m+2
m+6) ... (ex m+1-esima istruzione) |
* in tutti i casi vanno modificati anche gli eventuali
GOTO ... e THEN ... presenti in parti del programma che indirizzano a linee
di programma di cui è cambiato il numero d'ordine.
Più avanti approfondiremo l'analisi della equivalenza fra i diversi
formalismi proposti per il concetto di algoritmo. Incominciamo ad osservare
che:
| F è MR-calcolabile (calcolabile con una macchina a registri) | => | F è TP-calcolabile (calcolabile con un programma
di Turing-Post). | |
Traccia Dim: sia f a k input e 1 output calcolata dall'MR-programma
P1; dobbiamo costruire un TP-programma P2 che trasformi ...0 'i1' 0 'i2' 0 ... 0 'ik' 0 ...
in ...0 'f(i1,...,ik)' 0 ... (i1, ...,ik
corrispondono ai contenuti di R1, ...,Rk e f(i1,...,ik)
a quello di R0); ogni istruzione di P1 sarà tradotta
in istruzioni nel TP-linguaggio per posizionare il lettore su ij
se Rj è il registro considerato nell'istruzione (basta
spostarsi a sinistra fino a che si incontrano 2 "0", poi spostarsi a destra
fino a superare j+1 "0") e per aggiungere un "1" e spostare il seguito
tutto a destra di una cella se l'istruzione è PRINT 1 o ...
4. IL CALCOLO EQUAZIONALE (Herbrand e Gödel, 1934, rivisto
da Kleene, 1936)
| Idea. Dato: |
{ |
0! = 1 |
|
|
|
|
(n+1)! = n!·(n+1) |
|
|
|
|
per calcolare
3! si fa: |
(a) 3! = 2!·3
(b) 2! = 1!·2
(c) 1! = 0!·1
(d) 0! = 1 |
|
(e) 1! = 1·1 = 1
(f) 2! = 1·2 = 2
(g) 3! = 2·3 = 6 | |
| (a)-(c) le abbiamo ottenute dalla seconda equazione del sistema "sostituendo" 2, 1 e 0 a n. (e) la abbiamo ottenuta da (c) e (d): in (c) abbiamo "rimpiazzato" 0! col termine ad esso eguagliato da (d). Analogamente abbiamo ottenuto (f) da (b) ed (e), e (g) da (a) ed (f). |
Segni:
x y z w S f g
h k 0 = ' '
Simboli:
costante:
0
simbolo relazionale:
=
variabili:
x y z w x' y' z' w'
x'' y'' z'' w'' ..., in breve:
x y z w xi yi zi wi (i IN*)
IN*)
[si sarebbe potuta usare solo "x"; l'uso di più
lettere facilita la lettura rispetto al solo uso di pedici]
simboli funzionali:
S (a 1 posto)
fn gn
hn kn fin
gin hin
kin (i IN*) (a n posti, n
IN*) (a n posti, n IN*)
[abbreviazioni di: f', f", ecc.]
IN*)
[abbreviazioni di: f', f", ecc.]
Atomi:
variabili e costanti
Termini:
atomi o espressioni del tipo φt1
...tn (φ simbolo funzionale a n posti,
t1, ..., tn termini, n IN*)
IN*)
Equazioni:
espressioni del tipo t1 = t2
(t1, t2 termini)
[i, n, φ t1 , t2 ... sono chiamati metavariabili in quanto non sono oggetti del linguaggio del calcolo
equazionale ma del linguaggio con cui lo descriviamo)
Abbreviazioni:
# invece di SS...S0 (n occorrenze
di S) scriveremo n (o anche n, se non vi sono ambiguità).
# invece di fin t1
...tn scriveremo fi(t1 ...tn)
(parentesi e virgole implicitamente determinano il numero degli argomenti);
abbreviazioni analoghe per gli altri simboli funzionali
Esercizio. Supponiamo che +, *, – siano simboli funzionali a due posti; traduci, scrivendo +xy come x+y, ecc. e introducendo parentesi, il termine – + x * y z w [soluzione]
Regola di sostituzione (R1):
t1 = t2 | R1
t1 = t2 [v  n]
n]
(t1, t2 termini, v variabile, n IN;
con [α
IN;
con [α  β]
indichiamo la riscrittura della espressione a sinistra di "[" con β
al posto di α: α
"diventa" β).
β]
indichiamo la riscrittura della espressione a sinistra di "[" con β
al posto di α: α
"diventa" β).
Regola di rimpiazzamento (R2):
t1 = t2 , φ(i1,
..., in) = m | R2
t1 = t2 [φ(i1
...in)  m]
m]
(t1, t2 termini, φ
simb. funz., i1, ..., in , m IN)
IN)
Un'equazione E deriva da un insieme di equazioni Σ
(Σ | E) se si può
determinare una sequenza di equazioni E1, ..., En
tali che En sia E e per ogni i (1≤ i ≤ n)
Ei sia in Σ o esista j<i t.c.
Ej | R1 Ei o esistano
j, k < i t.c. Ej, Ek | R2
Ei.
Sia F una funzione a n input e 1 output in IN, sia φ
un simbolo funzionale a n posti e Σ un sistema
di equazioni. (Σ, φ)
calcola F se per ogni i1 ,...,in, m IN
IN
Σ |
φ(i1, ..., in) = m
sse F(i1, ..., in) è definito
e uguale a m.
Esempio:
| Σ = {f(x,0)=x, f(x,Sy)=Sf(x,y)}, che possiamo
scrivere anche: |
{ |
f(x,0) = x |
(a) |
|
f(x,Sy) = Sf(x,y) |
(b) |
Σ | f(1,2) = 3 |
1) (b) |
|
|
2) f(1,2) = Sf(1,1) |
da 1) per R1 |
|
3) f(1,1) = Sf(1,0) |
da 1) per R1 |
|
4) (a) |
|
|
5) f(1,0) = 1 |
da 4) per R1 |
|
6) f(1,1) = 2 |
da 3), 5) per R2 |
|
7) f(1,2) = 3 |
da 2), 6) per R2 |
(Σ,f) calcola la addizione.
({f(x,0) = x, f(x,Sy) = Sf(x,y), g(x,0) = 0, g(x,Sy) = f(g(x,y),x)},
g) calcola la moltiplicazione.
({f(x,0) = x, f(Sx,Sy) = f(x,y)}, f) calcola la sottrazione; è
una funzione parziale (è definita solo se il primo input è
maggiore o uguale al secondo)
({f(x,0) = x, f(Sx,Sy) = f(x,y), f(0,x) = 0}, f) calcola la sottrazione
"non-negativa" ( )
)
({f(x,0) = 0, f(0,Sx) = 1, f(Sx,Sy) = f(x,y)}, f) calcola la funzione
caratteristica di "<".
Esercizio. Sia Σ = {f(x,0) = x, f(x,Sy) = Sf(x,y), g(0) = 0, g(Sx) = f(g(x),x)}. Che cosa calcola (Σ,g)? [soluzione]
Questo approccio al concetto di "calcolabilità"
è diverso dai precedenti; non viene esibito un procedimento esplicito.
Anche se per gli esempi più semplici di funzioni intuitivamente
calcolabili siamo in grado di dare una descrizione con tutti i formalimi
finora visti, non è facile comprendere come dimostrare in generale
che, ad es., una funzione è MR-calcolabile sse
è CE-calcolabile (calcolabile con il calcolo equazionale).
Su ciò ci soffermeremo più avanti.
5. FUNZIONI RICORSIVE
Un ulteriore approccio al concetto di calcolabilità consiste
nel considerare l'insieme così definito:
| |
la più piccola classe che contiene +,  , × (cioè addizione, sottrazione
non-negativa e moltiplicazione tra numeri naturali), la funzione successore e le funzioni
proiezione e che è chiusa rispetto alla composizione e alla minimizzazione. , × (cioè addizione, sottrazione
non-negativa e moltiplicazione tra numeri naturali), la funzione successore e le funzioni
proiezione e che è chiusa rispetto alla composizione e alla minimizzazione. |
[ Data G totale a n+1 posti, dicesi funzione definita per minimizzazione (o minimalizzazione o μ-ricorsione)
a partire da G la funzione F che a x1,..., xn associa min{y / G(x1,...,
xn,y) = 0} (scritto anche o μy(G(x1,...,xn,y) = 0)]
Esempi:
– Se S è la funzione successore, x  S(S(x
S(S(x x)) è x
x)) è x  2
2
– (x,y)  μz(S(x)
μz(S(x) y×S(z)=0) è la divisione intera: x\y = INT(x/y).
y×S(z)=0) è la divisione intera: x\y = INT(x/y).
Gli elementi di questo insieme vengono chiamati funzioni
ricorsive.
Una relazione R(x1,..., xn) tra numeri naturali
viene detta ricorsiva se è tale la sua funzione caratteristica.
Il termine si adatterebbe meglio al caso del calcolo
equazionale (infatti la definizione di una funzione F [una relazione
R] viene chiamata ricorsiva quando impiega una uguaglianza [una
equivalenza] in cui F [R] compare sia a primo che a secondo membro), ma,
data la coincidenza di questa classe con quella delle funzioni CE-calcolabili,
...
In generale spesso si parla di funzioni ricorsive come
sinonimo di funzioni calcolabili. C'è chi restringe l'uso alle funzioni
definite per ogni input, e chiama ricorsive parziali la classe più
generale comprendente anche quelle non sempre definite; gli altri (noi
tra questi) chiamano ricorsive totali le funzioni definite per ogni
input.
Nota 1. Si può dimostrare che la ricorsione primitiva
F a n input è definita per ricorsione da G, a n-1 input, e H, a n+1 input, se F(x1,...,xn,0) = G(x1,...,xn) e F(x1,...,xn,y+1) = H(x1,...,xn,y,F(x1,...,xn,y) è ottenibile a partire dalle funzioni "base" (+, ..., proiezioni)
con composizione e minimizzazione.
Nota 2. La ricorsione primitiva (o definizione
induttiva), è, in pratica, un caso particolare di definizione
ricorsiva (cioè formalizzabile col calcolo equazionale) in cui il simbolo funzionale che si sta introducendo è
applicato nel secondo membro ad argomenti di complessità minore
rispetto a quelli a cui è applicato nel primo membro.
Nota 3. Nella definizione di funzione ricorsiva si possono omettere +,  e × dalle funzioni base, aggiungendo la funzione "zero"
(n
e × dalle funzioni base, aggiungendo la funzione "zero"
(n  0) e la condizione di chiusura rispetto alla ricorsione primitiva.
0) e la condizione di chiusura rispetto alla ricorsione primitiva.
Nota 4. Se si mette la ricorsione primitiva al posto della minimizzazione si ottiene l'insieme delle funzioni primitive ricorsive. Queste sono tutte totali. Tuttavia esistono funzioni ricorsive totali che non sono primitive ricorsive (ciò è legato alle considerazioni svolte in Nota 2).
Rispetto al calcolo equazionale, questo approccio
è più intuitivamente "meccanizzabile". Ad es. è facile
realizzare MR-programmi per calcolare funzioni ricorsive:
è semplice realizzare MR-programmi
per tutte le funzioni base,
la composizione può essere ottenuta
concatenando i programmi che calcolano le funzioni componende dopo averne
opportunamente modificato gli indici dei registri e le etichette delle istruzioni di
salto (e aver man mano introdotto azzeramenti dei registri usati nei precedenti calcoli di funzione),
la minimizzazione può essere ottenuta
con un semplice ciclo.
indice

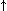 per "il programma P con input v non si
arresta"
per "il programma P con input v non si
arresta"
 w per "il programma P con input
v si arresta e ha come output w" (stringa di output:
massima porzione del nastro nella sua configurazione finale che ha "1"
come primo e ultimo carattere)
w per "il programma P con input
v si arresta e ha come output w" (stringa di output:
massima porzione del nastro nella sua configurazione finale che ha "1"
come primo e ultimo carattere)

 1 Ri = 0 IF Ri=
0 THEN n (i, n naturali)
1 Ri = 0 IF Ri=
0 THEN n (i, n naturali) S(S(x
S(S(x