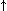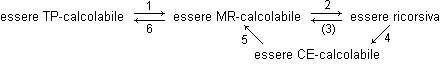
6. EQUIVALENZE - SOTTOPROGRAMMI RICORSIVI
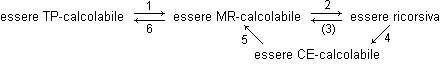
Abbiamo già considerato l'implicazione 6 nella sezione 3 e l'implicazione 3 nella sezione 5 (nello schema soprastante 3 è tra parentesi perchè tale implicazione consegue da 2, 4 e 5). Consideriamo le altre implicazioni.
(4): è facile definire sistemi di equazioni per calcolare le funzioni ricorsive base; le funzoni CE-calcolabili sono evidentemente chiuse rispetto alla composizione; vediamone la chiusura rispetto alla minimizzazione:
data G totale a n+1 posti calcolata da (Σ,
g), F: x1,..., xn  min{y/G(y, x1,...,
xn) = 0} è calcolata da (Σ', f) dove
Σ' è ottenuto da Σ
aggiungendo le equazioni del sistema che calcola "·" e (usando "·"
invece di una lettera funzionale, per comodità): |
| h((0, x1,..., xn) = 1, h(Sy, x1,..., xn) = h(y, x1,..., xn)·g(y, x1,..., xn), |
| [ovvero h(Sy, x1,..., xn) "è" g(0, x1,..., xn)·g(1, x1,..., xn)· ... ·g(y, x1,..., xn)] |
| k(Sx,0,y) = y, |
| f(x1,..., xn) = k(h(y, x1,..., xn), h(Sy, x1,..., xn), y) |
| [ovvero f è definita se g(0, x1,..., xn), ... ,g(y-1, x1,..., xn) sono diversi da 0 e g(y, x1,..., xn) è 0] |
(1), (2): Su esempi non troppo complessi è abbastanza facile capire come traformare un TP-programma che calcola una funzione in una sequenza di istruzioni MR, così come trasformane un MR-programma nella definizione di una funzione risorsiva. Una descrizione generale dei procedimenti di traduzione non è banale, e non la affronteremo.
(5): Anche questa dimostrazione non è banale,
ma, anche senza vederela in dettaglio, cercheremo di farcene un'idea in
quanto ciò ci consentirà di capire come opera un linguaggio
di programmazione evoluto (come i Basic strutturati, il Pascal o il C)
nel tradurre in linguaggio macchina una procedura ricorsiva (problema che,
nell'essenza dei sui aspetti concettuali, era di fatto già stato
affrontato negli anni 30 dimostrando l'equivalenza tra macchine di Turing
e calcolo equazionale).
Più precisamente ci accontentiamo di vedere come
è possibile tradurre le definizioni ricorsive in un linguaggio che
non ammette sottoprogrammi con chiamate ricorsive. Supponiamo che tale
linguaggio ammetta l'uso di variabili indiciate e abbia altre semplci estensioni
rispetto al linguaggio delle macchine a registri (avvicinandolo ulteriormente
ai linguaggi Basic).
k=0 C(n,k) / k=1 n=0 1 / k=2 n=1 1 1 / k=3 n=2 1 2 1 / k=4 n=3 1 3 3 1 / n=4 1 4 6 4 1 |
Consideriamo ad es. il calcolo dei coefficienti binomiali
mediante la definizione ricorsiva:
In Basic strutturato avrebbe assunto la forma: |
| 1 INPUT "n,k"; n,k
CALL CBIN(n,k,c) PRINT "c ="; c GOTO 1 |
SUB CBIN(n,k,c)
IF k=0 THEN c=1 : EXIT SUB IF k=n THEN c=1 : EXIT SUB CALL CBIN(n-1,k-1,a) CALL CBIN(n-1,k,c) c=a+c END SUB |
||
| [Nota: nella intestazione della definizione della procedura ("sub") tra parentesi sono indicati i "parametri" formali; conveniamo che le variabili che compaiono nella definizione siano "locali" (come accade ad es. in QBasic - se operi da Windows, se vuoi, clicca qui per poter aprire dalla sottofinestra sinistra della finestra che apparirà il QBasic - vedi dalla stessa finestra le informazioni sulle applicazioni a console per capire come incollare nella finestra di lista programmi selezionati e copiati]); nella chiamata ("call") tra parentesi sono indicati gli "argomenti" che vengono sostituiti ai parametri; se si omette "call" si può omettere anche la coppia di parentesi; in altri Basic strutturati (ad es. in RapidQBasic, per la programmazione ad oggetti) per rendere locali le variabili interne al sub occorrerebbe dichiararle, ad es. con un'istruzione DIM]. | |||
Senza ricorsione può essere realizzato così (abbiamo memorizzato n e k in n0 e k0 perché durante l'esecuzione del sottoprogramma 100-111 il contenuto di n e k viene modificato):
1 INPUT "n,k"; n, k
2 n0=n: k0=k: L=3: GOTO 100
3 PRINT "c("; n0; ","; k0; ") ="; c
4 GOTO 1
100 i=-1
101 i=i+1: L(i)=L
102 IF k=0 THEN c=1: GOTO 108
103 IF k=n THEN c=1: GOTO 108
104 n(i)=n: k(i)=k: n=n-1: k=k-1: L=105: GOTO 101
105 a(i)=c
106 n=n(i)-1: k=k(i): L=107: GOTO 101
107 c=a(i)+c
108 L=L(i): i=i-1
109 IF L=3 THEN GOTO 3
110 IF L=105 THEN GOTO 105
111 IF L=107 THEN GOTO 107
|
n,k? 4,2 i n k 0 4 2 1 3 1 2 2 0 2 2 1 3 1 0 3 1 1 1 3 2 2 2 1 3 1 0 3 1 1 2 2 2 c( 4 , 2 ) = 6 n,k? 4,0 i n k 0 4 0 c( 4 , 0 ) = 1 |
A destra è illustrata l'evoluzione del calcolo, così come può essere esaminata inserendo PRINT i; n; k dopo la linea 101 (e PRINT " i n k" dopo la linea 100). La variabile i tiene conto del livello di "nidificazione" della chiamata, la variabile indiciata L( ) memorizza il punto in cui occorre ritornare dopo la chiamata ricorsiva, n( ), k( ) e a( ) memorizzano i valori degli argomenti n e k e della variabile locale a prima che vengano modificati nel corso di una chiamata ricorsiva.
Un programma per il calcolo della funzione fattoriale che traduca la definizione ricorsiva: f(0)=1, f(Sx)=f(x)·Sx, che in Basic sarebbe stato realizzabile usando il sottoprogramma sotto a sinistra, può essere realizzato nel modo indicato al centro. A destra è illustrata l'evoluzione del calcolo.
SUB FAT(n,f) IF n=0 THEN f=1: EXIT SUB CALL FAT(n-1,f) f=f*n END SUB |
1 INPUT "n"; n 2 n0=n: L=3: GOTO 100 3 PRINT n0;"! ="; F 4 GOTO 1 100 i=-1 101 i=i+1: L(i)=L 102 IF n=0 THEN F=1: GOTO 106 103 n(i)=n: n=n-1: L=104: GOTO 101 104 n=n(i) 105 F=F*n 106 L=L(i) : i=i-1 107 IF L=3 THEN GOTO 3 108 IF L=104 THEN GOTO 104 |
n? 0 i n 0 0 0 ! = 1 n? 3 i n 0 3 1 2 2 1 3 0 3 ! = 6 |
Massimo comune divisore (con sottrazioni successive): a sinistra la procedura ricorsiva, a destra la versione senza ricorsione, sotto a sinistra l'evoluzione del calcolo.
SUB MAXDIV(m,n,mcd) IF m>n THEN MAXDIV m-n,n,mcd: EXIT SUB IF n>m THEN MAXDIV m,n-m,mcd: EXIT SUB mcd=m END SUB | |
m,n? 120,36 i 0 1 2 3 4 5 m.c.d.(m,n) = 12 |
1 INPUT "m,n"; m,n 2 m0=m: n0=n: L=3: GOTO 100 3 PRINT "m.c.d.(m,n) ="; mcd 4 GOTO 1 100 i=-1 101 i=i+1: L(i)=L 102 IF m>n THEN m=m-n: L=105: GOTO 101 103 IF n>m THEN n=n-m: L=105: GOTO 101 104 mcd=m 105 L=L(i): i=i-1 106 IF L=3 THEN GOTO 3 107 IF L=105 THEN GOTO 105 |
Negli esempi abbiamo utilizzato variabili indiciate solo per le memorizzazioni essenziali (nel caso dell'ultimo esempio non abbiamo memorizzato i valori di alcuna variabile: non serviva in quanto dopo ogni chiamata ricorsiva si esce dalla procedura con un Exit Sub). Più meccanicamente avremmo potuto man mano memorizzare prima di ogni chiamata ricorsiva i valori di tutte le variabili.
ESERCIZI
1) Dimostrare che la funzione max che a (M,N) associa il massimo tra M e N è ricorsiva. [risp.]
2) Esiste f: N 
N non ricorsiva? [risp.]
3) Dove sta l'errore nella seguente dimostrazione?
Le funzioni ricorsive non sono numerabili in quanto se F0, F1, F2, ... fosse una loro enumerazione la funzione F così definita:
F(0)=F0(0)+1, ..., F(n)=Fn(n)+1, ...
sarebbe definita costruttivamente, ma non potrebbe stare nell'elenco in quanto sarebbe diversa da ogni Fn: se F fosse Fi avremmo che F(i)=F(i)+1. [risp.]
7. IL PROGRAMMA/CALCOLATORE UNIVERSALE
# Concetto di codice: procedimento meccanico
per trasformare le espressioni di un linguaggio formale L1
in espressioni di un linguaggio formale L2 tale che:
la funzione F: {espressioni di L1} 
{in espressioni di L2} da esso definita sia iniettiva,
l'insieme E immagine di F, cioè F({espressioni di L1}), sia decidibile (cioè esista un procedimento meccanico per stabilire se una espressione di L2 appartiene o no a E),
la funzione inversa G (o, meglio, la funzione G: E
{espressioni di L1} tale che, per ogni α in E, G(F(α))
= α) sia anch'essa descrivibile con un procedimento
meccanico.
L'applicazione di F si chiama codifica, quella di G si
chiama decodifica. La gödelizzazione può essere interpretata
come una codifica in un linguaggio formale per descrivere i numeri naturali
(ad es. quello avente per alfabeto {0, 1, ..., 9}).
# Possibilità di codificare i programmi sotto forma di stringhe di 0 e 1: vedi sotto (data una sequenza di bit siamo in grado di capire se si tratta o no della codifica di un programma ed eventualmente di risalire al programma). Usiamo [P] per la codifica del programma P.
# Il calcolatore (o programma) universale U (anticipazione della attuale idea di computer: macchina programmabile, cioè programmata per accettare come input programmi):
Esistono concetti analoghi per gli altri formalismi. Consideriamo ad esempio il calcolo equazionale.
Si possono codificare numericamente tutte le possibili coppie (Σ,f) del calcolo equazionale; basta, ad esempio, generare in ordine alfabetico (fissato un qualunque ordinamento tra l'insieme finito di segni impiegato) tulle le coppie cosituite da 10 segni - come ({0=0},f') -, poi quelle costituite da 11, ...e si può associare 1 alla prima di esse, 2 alla seconda, e così via); indichiamo con [Σ,f] il numero codice di (Σ,f).
Analogamente si possono codificare numericamente le sequenze di numeri naturali; si può ad es. considerare la virgola "," come 11° simbolo e quindi ordinare le sequenze per lunghezza e alfabeticamente (cioè così: 0 1 ... 9 10 ... 99 0,0 0,1 0,9 100 ... 199 1,0 1,1 ...); indichiamo con [i1, ...,in] la codifica della sequenza i1, ...,in.
Poi si può definire un opportuno sistema Σ tale che (Σ,f) calcoli una funzione U a 2 input che abbia questa proprietà:
se F a n input è calcolata da (Σ,f),
# Simulazione del programma universale sugli attuali computer (si tratta del programma Turing a cui, da Windows, puoi accedere cliccando QUI):
CALCOLATORE UNIVERSALE U di Turing(-Post), programmato in modo da simulare qualunque calcolatore di Turing C: se a U do` in input la codifica del programma P che regola C e una stringa nella forma: CodificaP + Stringa esso si comporta come C di fronte all'input: Stringa Per far procedere l'esecuzione si preme 'a capo', per ARRESTARLA si batte F Durante l'esecuzione viene visualizzata una porzione variabile di nastro, piu` o meno centrata sulla cella che U sta esaminando. Tale cella e` indicata in giallo o, nella versione in B/N, con 'u' se il suo contenuto e` 1 (uno) e con 'z' se il suo contenuto e` 0 (zero). In pratica, il comando VAI A SINISTRA/destra viene visualizzato come uno SPOSTA A DESTRA/sinistra il nastro. Codifica 000 print 0 001 print 1 010 go left 011 go right istruzioni 100 stop 110..(n 1)..0 go to step n if 1 is scanned 101..(n 0)..1 go to step n if 0 is scanned Codifica programma: 1 + CodificaIstruzione1 + CodificaIstruzione2 + ... + 111 |
DUPLICATORE (vedi sezione 2):
lista in esame 10000101101100010111101111100010111101010011111
n.bit= 47
000 1 print 0
010 2 go left
110110 3 go to step 2 if 1 is scanned
001 4 print 1
011 5 go right
110111110 6 go to step 5 if 1 is scanned
001 7 print 1
011 8 go right
11010 9 go to step 1 if 1 is scanned
100 10 stop
input: 11
000000000000000000000000000000000u10000000000000000000000000000
p 0 000000000000000000000000000000000z10000000000000000000000000000
go L 000000000000000000000000000000000z01000000000000000000000000000 if 1 then ...
p 1 000000000000000000000000000000000u01000000000000000000000000000
go R 000000000000000000000000000000001z10000000000000000000000000000 if 1 then ...
p 1 000000000000000000000000000000001u10000000000000000000000000000
go R 000000000000000000000000000000011u00000000000000000000000000000 if 1 then ...
p 0 000000000000000000000000000000011z00000000000000000000000000000
go L 000000000000000000000000000000001u00000000000000000000000000000 if 1 then ...
go L 000000000000000000000000000000000u10000000000000000000000000000 if 1 then ...
go L 000000000000000000000000000000000z11000000000000000000000000000 if 1 then ...
p 1 000000000000000000000000000000000u11000000000000000000000000000
go R 000000000000000000000000000000001u10000000000000000000000000000 if 1 then ...
go R 000000000000000000000000000000011u00000000000000000000000000000 if 1 then ...
go R 000000000000000000000000000000111z00000000000000000000000000000 if 1 then ...
p 1 000000000000000000000000000000111u00000000000000000000000000000
go R 000000000000000000000000000001111z00000000000000000000000000000 if 1 then ...
stop 000000000000000000000000000001111z00000000000000000000000000000
output: 1111
TRIPLICATORE: come può essere realizzato?
lista in esame 1000010110110001010001011110111111100010111101010011111 n.bit= 55 000 1 print 0 010 2 go left 110110 3 go to step 2 if 1 is scanned 001 4 print 1 010 5 go left 001 6 print 1 011 7 go right 11011111110 8 go to step 7 if 1 is scanned 001 9 print 1 011 10 go right 11010 11 go to step 1 if 1 is scanned 100 12 stop
Programma che a seconda dell'input CONVERGE O NO (predecessore):
lista in esame 1011101010100001001111
n.bit= 22
011 1 go right
10101 2 go to step 1 if 0 is scanned
010 3 go left
000 4 print 0
100 5 stop
input: 1
00000000000000000000000000000000u0000000000000000000000000
go R 00000000000000000000000000000001z0000000000000000000000000 if 0 then ...
go R 00000000000000000000000000000010z0000000000000000000000000 if 0 then ...
go R 00000000000000000000000000000100z0000000000000000000000000 if 0 then ...
...
lista in esame 101110101010000100111111
input: 111
00000000000000000000000000000000u1100000000000000000000000
go R 00000000000000000000000000000001u1000000000000000000000000 if 0 then ...
go L 00000000000000000000000000000000u1100000000000000000000000
p 0 00000000000000000000000000000000z1100000000000000000000000
stop 00000000000000000000000000000000z1100000000000000000000000
output: 11
DIFFERENZA (M-N definita solo se N≤M):
Idea: togliere man mano un "1" da ciascuna delle due stringhe di "1", non facendo arrestare il programma se si annulla prima la stringa a sinistra.
lista in esame 10111101001110100010000111010000000000000010101010000000010000101101110 101000000000000011001111111011 n.bit= 101 011 1 go right 11010 2 go to step 1 if 1 is scanned 011 3 go right 1010001 4 go to step 3 if 0 is scanned 000 5 print 0 011 6 go right 101000000000000001 7 go to step 14 if 0 is scanned 010 8 go left 101000000001 9 go to step 8 if 0 is scanned 000 10 print 0 010 11 go left 1101110 12 go to step 3 if 1 is scanned 10100000000000001 13 go to step 13 if 0 is scanned 100 14 stop input: 1111011 (cioè 31) 1-2 passa a destra finché incontri 1 3-4 passa a destra finché incontri 0 5-7 cancella il primo 1, vai a destra, se non ce n'è altri fermati 8-9 passa a sinistra finché incontri 0 10-12 cancella il primo 1, vai a sinistra, se ce n'è altri riparti 13 altrimenti vai in loop 000000000000000000000000000000000u11101100000000000000000000 go R 000000000000000000000000000000001u11011000000000000000000000 go R 000000000000000000000000000000011u10110000000000000000000000 go R 000000000000000000000000000000111u01100000000000000000000000 go R 000000000000000000000000000001111z11000000000000000000000000 go R 000000000000000000000000000011110u10000000000000000000000000 p 0 000000000000000000000000000011110z10000000000000000000000000 go R 000000000000000000000000000111100u00000000000000000000000000 go L 000000000000000000000000000011110z10000000000000000000000000 go L 000000000000000000000000000001111z01000000000000000000000000 go L 000000000000000000000000000000111u00100000000000000000000000 p 0 000000000000000000000000000000111z00100000000000000000000000 go L 000000000000000000000000000000011u00010000000000000000000000 go R 000000000000000000000000000000111z00100000000000000000000000 go R 000000000000000000000000000001110z01000000000000000000000000 go R 000000000000000000000000000011100z10000000000000000000000000 go R 000000000000000000000000000111000u00000000000000000000000000 p 0 000000000000000000000000000111000z00000000000000000000000000 go R 000000000000000000000000001110000z00000000000000000000000000 stop 000000000000000000000000001110000z00000000000000000000000000 output: 111 input: 1011 (cioè 01) 000000000000000000000000000000000u01100000000000000000000000 go R 000000000000000000000000000000001z11000000000000000000000000 go R 000000000000000000000000000000010u10000000000000000000000000 p 0 000000000000000000000000000000010z10000000000000000000000000 go R 000000000000000000000000000000100u00000000000000000000000000 go L 000000000000000000000000000000010z10000000000000000000000000 go L 000000000000000000000000000000001z01000000000000000000000000 go L 000000000000000000000000000000000u00100000000000000000000000 p 0 000000000000000000000000000000000z00100000000000000000000000 go L 000000000000000000000000000000000z00010000000000000000000000 if 1 then ... if 0 then ... if 0 then ... ... Quale funzione a 2 input calcola il programma seguente? 1 go right 2 go to step 1 if 1 is scanned 3 go right 4 go to step 3 if 0 is scanned 5 print 0 6 go right 7 go to step 13 if 0 is scanned 8 go left 9 go to step 8 if 0 is scanned 10 print 0 11 go left 12 go to step 3 if 1 is scanned 13 stop
8. INDECIDIBILITÀ DELL'HALTING PROBLEM (problema della fermata)
Esiste la possibilità di stabilire a priori (con un opportuno programma), presi comunque un programma P e una stringa di input v, se P(v)
o P(v)
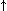? Vedremo che la risposta è negativa. Vedremo, in particolare, che non esiste un programma per decidere ciò nel caso in cui si fissi U come P. A maggior ragione non ne esiste uno che sia in grado di farlo per un generico P.
Ipotesi: esite H tale che H(v) 1 se U(v), H(v) 0 se U(v).
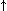Idea: a partire da questa ipotesi arrivare all'assurdo dell'esistenza di un programma W tale che: W([W]) sse W([W]).
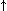Posso costruire un programma W che implementi il seguente algoritmo (descritto in stile "basic": "+" è la concatenazione; "$" specifica le variabili stringa):
10 |
INPUT v$ IF H(v$+v$) 1 THEN GOTO 10
|
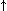sse H([W]+[W]) 0 sse U([W]+[W]) sse W([W])