9. ASSIOMATIZZABILITÀ, DECIDIBILITÀ, COMPLETEZZA

    Vedremo come dal teorema di indecidibilità del problema dell'arresto si possano dedurre risultati limitativi nel campo della logica matematica; se si riflette sui legami tra procedimento di calcolo e procedimento dimostrativo, la cosa non sorprende. Prima di affrontare questi risultati, richiamiamo (precisando alla luce del concetto di calcolabilità) alcune nozioni e alcuni teoremi di logica  (vedi  qui  per il richiamo di una possibile assiomatizzazione del calcolo dei predicati e una introduzione ai significato di prova o derivazione o dimostrazione e di teorema).

#0    Due parole usate spesso: sintassi e semantica. Con la prima, in uso da più di 2000 anni, si intende lo studio della grammatica, con la seconda, in uso dal XIX secolo, si intende lo studio del significato.  In logica matematica, la prima parola si riferisce al procedimento con cui vengono costruite le formule e a come a partire da certe formule se ne possono ottenere altre mediante opportune regole di trasformazione, la seconda si riferisce al procedimento con cui vengono associate alle formule i loro valori di verità (vero o falso).

#1    una nozione di derivazione |— (in un generico sistema formale, costituito da espressioni "costruite" con un insieme finito di segni [l'uso di indici naturali è riconducibile alla ripetizione di un apice o un pedice] in modo tale che vi sia un procedimento meccanico per stabilire se una sequenza di segni è o no una espressione, da un apparato deduttivo "meccanico", ...: vedi sezione 1) è completa se (def) per ogni insieme E di formule e ogni formula A, quando A è valida in E (cioè vera in ogni modello di E, ossia in ogni struttura che dia significato alle formule di E) si ha anche E|—A (vedi anche il successivo #10).

#2   Il calcolo proposizionale (vedi  qui ) è completo. Le tavole di verità sono funzioni calcolabili; quindi il calcolo proposizionale è decidibile, cioè lo è l'insieme delle sue conseguenze (fissato un "universo" numerabile, un insieme E è decidibile se si può stabilire meccanicamente se un elemento dell'universo appartiene o no a E, cioè se, fissata una codifica in IN dell'universo, la funzione caratteristica della immagine di E mediante la codifica è una funzione ricorsiva - se l'universo è l'insieme delle espressioni di un linguaggio formale, una codifica in IN viene chiamata anche gödelizzazione).

#3   La logica del 1° ordine è completa (1° t. compl. di Gödel, 1930). Non è completa la logica del 2° ordine (accanto alle variabili individuali x, y, z, ... ci cono variabili predicative X, Y, Z, ... - interpretate come insiemi -; sono formule atomiche anche X(t), ... ; X(t) è interpretato come "l'elemento associato a t appartiene all'insieme associato a X"; ...): per essa conseguenza logica e dimostrazione non coincidono.

#4   Un insieme di formule E è consistente (o non contraddittorio o coerente) se (def) esiste una formula A tale che non E|—A, cioè che non sta in Con(E) (insieme delle conseguenze di E, cioè {A/E|—A}).

#5   Un insieme di formule E è una teoria se (def) è chiuso rispetto a Con.

#6   Una teoria T è assiomatizzabile se esiste un insieme decidibile di formule E (assiomi "non logici") tale che T = Con(E).

#7   Una teoria T è categorica se (def) tutti i suoi modelli sono tra loro isomorfi.

#8   Ovviamente, ogni teoria del 1° ordine che abbia un modello è consistente. Vale anche il viceversa. Abbiamo infatti che:  una teoria del 1° ordine è consistente sse ha un modello (2° t. compl. di Gödel ). Abbiamo, anche, che ha un modello sse lo ha ogni sua sottoteoria finitamente assiomatizzabile (T. di compattezza).

#9   Una teoria del 1° ordine avente un modello infinito ha modelli di cardinalità α per ogni α  ₀. (t. di Löwenheim-Skolem, generalizzato). Quindi non esistono teorie del 1° ordine categoriche, a meno che non abbiano solo un modello finito.
[avremmo, ad es., che una descrizione assiomatica del 1° ordine dei numeri reali ha un modello numerabile!! - la cosa può sembrare assurda; lo appare meno se pensiamo la proprietà enunciata dal teorema come "avere un modello della stessa cardinalità del linguaggio"; in altre parole, nella pratica matematica lavoriamo effettivamente con al più una quantità numerabile di oggetti; in altre nuove parole: gli unici modelli reali di fatto sono quelli sintattici, che sono numerabili se il linguaggio è numerabile; in altre parole ancora, i numeri reali del modello numerabile non sono i "veri" numeri reali ma solo un insieme con le loro stesse proprietà insiemistiche]

#10   Una teoria T è completa se per ogni formula A si ha che T|—A o che T|—¬A. A per cui ciò non accada dicesi formula indecidibile (o indecisa). [si noti la differenza tra completezza di una teoria e completezza di un sistema di regole logiche (|—): vedi #1]

#11   Una teoria completa assiomatizzabile è decidibile.
[Se ci si pensa un attimo, la cosa appare evidente. Ecco, comunque, la traduzione argomentata di questa "evidenza". Sia T la teoria. Sia E decidibile tale che Con(E)=T. Costruita una macchina che genera in un certo ordine tutte le formule, grazie alla decidibilità di E posso costruire una macchina M che per ogni n individua tra le prime n formule gli elementi di E; sia E_n il loro insieme. A questo punto, per ogni formula A possiamo stabilire se sta in T così:
(1) sia n=1,
(2) verifico se in n passi riesco a derivare da E_n A oppure ¬A,
(3) se ho risposta affermativa mi fermo, altrimenti incremento n di 1 e vado al passo (2).
Poiché per la completezza A o ¬A è un teorema, prima o poi ottengo una risposta affermativa. Con questo procedimento posso stabilire se A è un teorema o no.]

#12   Ogni teoria consistente che estenda l'aritmetica del 1° ordine non è decidibile e, quindi, (1° t. di incompletezza di Gödel, 1931, nell'ipotesi di ω-consistenza, esteso da Rosser, nel 1936, all'ipotesi della semplice consistenza) non è completa. Gödel, invero, esibisce una formula dell'aritmetica del 1° ordine vera (nell'interpretazione standard) ma non dimostrabile.

#13   La parola "dimostrazione" (o "prova") è usata in due sensi diversi:  in un preciso significato definito formalmente e richiamato all'inizio di questo paragrafo (spesso indicato col termine "derivazione"),  in un altro senso per indicare una argomentazione formulata nel linguaggio comune (italiano o inglese, per esempio), integrato da vari termini tecnici, relativa ad una certa teoria formale, come ad esempio l'argomentazione presente in #11. Questa secondo tipo di dimostrazioni a volte sono distinte dalle prime col termine metadimostrazioni, e i relativi teoremi sono chiamati metateoremi.

   Osserviamo che negli anni '20 il concetto di "completezza" di una teoria era confuso con quelli di categoricità e di decidibilità. E` successiva alla dimostrazione dei teoremi di incompletezza di Gödel la associazione del termine "completezza" (Menger, anni '30) a ciò che oggi noi intendiamo con tale termine.

    La prima cosa che affronteremo è come, grazie al teorema di indecidibilità dell'arresto sia possibile ottenere una risultato di incompletezza da un punto di vista diverso, per certi aspetti più generale, rispetto al 1° teorema di incompletezza di Gödel (vedi #12):

TEOREMA DI INCOMPLETEZZA DI "TURING-GÖDEL"
Comunque prenda una teoria assiomatizzabile T in cui si possano dimostrare formule del tipo P(v)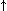, esistono P,v tali che da una parte sia vero che P(v) 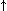e, dall'altra, non T|—P(v).
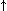Dim
   Sottointendiamo che le regole di derivazione siano "corrette" (quindi tali che se T|—P(v)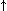 allora sia vero che P(v)).
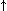Suppongo, per assurdo, che per ogni P e v tali che P(v)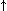 si abbia T|—P(v)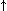. Fisso P e v.
-   genero in ordine tutte le possibili prove (ad es. considerando ogni sequenza di formule come un'unica espressione, mediante l'introduzione di un segno per delimitare una formula dalla successiva, mettendo queste espressioni in ordine di lunghezza e, in subordine, alfabetico e testando man mano se sono prove o no) e verifico per ciascuna se è o no una prova di P(v);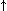
-   nel frattempo, in parallelo, eseguo P(v).
   In questo modo avrei un procedimento per risolvere il problema della fermata per P:
-   se P(v) prima o poi me ne accorgo (la macchina si ferma),
-   se P(v) prima o poi ne trovo una dimostrazione   
End Dim

    Nelle prossime sezioni dimostreremo un nuovo risultato limitativo, cioè che il calcolo dei predicati è indecidibile (Church e Turing, 1936). L'idea della dimostrazione è abbastanza semplice: tradurre il problema dell'arresto in un linguaggio del primo ordine e dedurre dalla sua indecidibilità l'esistenza di formule per cui non è possibile stabilire meccanicamente se sono teoremi o no. Per affrontare nei dettagli la dimostrazione può essere comodo ricondurre i programmi di Turing-Post alle originali macchine di Turing, che si prestano meglio a una traduzione in un linguaggio del 1° ordine.

10. MACCHINE DI TURING (TM) - versione originale

...	S0 S0 S0 Si Sj	...	Sk S0 S0 S0	...
	qh

#   nastro suddiviso in celle potenzialmente illimitato
#   in ogni cella c'è un carattere, cioè un simbolo scelto tra il simbolo "vuoto" S₀ e un insieme finito di simboli S₁, ..., S_n
#   solo una quantità finita di celle non è vuota (cioè ha un simbolo diverso da S₀)
#   una testina di lettura/scrittura si può spostare sul nastro e può assumere una quantità finita di stati interni q₁, q₂, ..., q_m
#   inizialmente la testina di lettura/scrittura è posizionata sulla prima (a sinistra) cella non vuota e è nello stato q₁
#   una quadrupla del tipo q_i S_j S_h q_k, se la testa di lettura/scrittura è nello stato q_i e legge il simbolo S_j, comanda la scrittura di S_h (al posto di S_j) e il cambiamento di stato da q_i a q_k
#   una quadrupla del tipo q_i S_j S q_h, se la testa di lettura/scrittura è nello stato q_i e legge il simbolo S_j, comanda lo spostamento della testa di lettura/scrittura di una cella a sinistra e il cambiamento di stato da q_i a q_h
#   una quadrupla del tipo q_i S_j D q_h, se ... , comanda ... a destra e ... da q_i a q_h

Macchina di Turing: insieme finito (non vuoto) di quadruple tali che non ve ne siano due che iniziano con gli stessi due simboli. La macchina si arresta quando non vi sono più azioni da compiere, cioè quando si arriva a uno stato q_i e si è posizionati su un simbolo S_j senza che vi siano quadruple inizianti con q_i S_j.

Esempio: macchina che trasforma una sequenza di 1 (1 è S1) in una sequenza con un solo 1 (rappresentando le funzioni come con i programmi di T.-P. - vedi sez. 2 - corrisponde alla funzione che a n associa 0).

q1 1 D q2 q2 1 S0 q1 q1 S0 D q2

1 1 1		1 1 1		1   1		1   1		1		1
1		2		1		2		1		2

Esercizio: quale funzione numerica a 2 input e 1 output calcola la seguente macchina (usiamo 0 per S₀): {q₁ 1 0 q₂, q₂ 0 D q₃, q₃ 1 D q₃, q₃ 0 1 q₄, q₄ 1 S q₄, q₄ 0 D q₅, q₅ 1 0 q₅}  [soluz.]

1 1 1   1 1		1 1   1 1		1 1   1 1
1		2		3

1 1   1 1		1 1   1 1		1 1 1 1 1
3		3		4

1 1 1 1 1		1 1 1 1 1		1 1 1 1 1
4		4		4

1 1 1 1 1		1 1 1 1
5		5

    Le macchine di Turing sono un esempio particolarmente semplice di automa finito (o automa a stati finiti), ossia una struttura tale che: (1) ad ogni istante essa assume uno tra un insieme finito di stati, (2) la transizione da uno stato all'altro è causata da un segnale di ingresso, (3) durante l'evoluzione tra due stati può emettere un segnale d'uscita, (4) gli insiemi dei possibili segnali di ingresso e di uscita sono finiti.

   È facile verificare la equivalenza della TM- calcolabilità con la TP-calcolabilità.
   Sia P un TP a N istuzioni. Alla i-ma istuzione associamo le quadruple  q_i  0  *  q_i+1  e  q_i  1  *  q_i+1  prendendo come * : 0 se l'struzione è PRINT 0, 1 se l'struzione è PRINT 1, D se l'struzione è GO RIGHT, S se l'struzione è GO LEFT.
   Se l'istruzione è STOP le associamo le quadruple  q_i  0  0  q_N+1  e  q_i  1  1  q_N+1.
   Se l'istruzione è GO TO STEP j IF 1 IS SCANNED le associamo le quadruple  q_i  0  0  q_i+1  e  q_i  1  1  q_j.
   Se è GO TO STEP j IF 0 IS SCANNED le associamo  q_i  1  1  q_i+1  e  q_i  0  0  q_j.
   L'insieme di queste quadruple costituisce una TM che calcola la stessa funzione eventualmente calcolata da P.
   L'implicazione opposta è dimostrabile in modo simile.

Esercizio Costruisci la macchina di Turing equivalente al seguente programma di TP e determina quale funzione IN → IN esso rappresenta. [soluz.]

1   go right
2   go to step 13 if 0 is scanned
3   go right
4   go to step 13 if 0 is scanned
5   go left
6   go to step 5 if 1 is scanned
7   go right
8   print 0
9   go right
10  print 0
11  go right
12  go to step 1 if 1 is scanned

    Esistono anche altri approcci al concetto di calcolabilità sviluppati negli anni 30 e 40, tutti equivalenti a quelli da noi considerati: logica combinatoria, λ-calcolo, algortimi di Markov, ...

11. PROBLEMI DI PAROLE

   Per tradurre in un linguaggio del 1° ordine il problema dell'arresto dovremo descrivere sotto forma di termini gli stati attraverso cui man mano passa una macchina di Turing, mediante un'opportuna relazione la trasformazione che porta da uno stato all'altro e mediante opportune formule le regole che governano questa trasformazione. Prima di fare ciò è utile introdurre un sistema volto a formalizzare le manipolazioni delle stringhe o, come si usa dire, le trasformazioni di parole.
   Consideriamo dunque il sistema formale così definito:

Simboli:  →  e un insieme finito di altri simboli, che chiameremo "lettere"
Parola (o termine): sequenza finita (o nulla: Λ) di lettere
Produzione (o formula): α → β con α e β parole
Regola di riflessione:  |— α → α
Regola di transizione: α → β, β → γ |— α → γ
Regola di rimpiazzamento (rimpiazzo π con τ in απβ): π → τ  |— απβ → ατβ

Dato Σ insieme finito di produzioni, poniamo Σ  |—  α →  β (da Σ deriva la produzione α →  β) se c'è una successione p₁, ..., p_n di produzioni tali che p_i sta in Σ o deriva da precedenti elementi della successione mediante una delle tre regole.
Un problema di parole è una questione del tipo: "da Σ deriva la produzione α → β?"

Esempio 1:
lettere: 1    Σ = {Λ → 11}
Sono derivabili tutte le produzioni Λ → 11...1 con un numero pari di "1":
(1)    Λ → 11   è in Σ
(2)   11 → 1111   per rimpiazzamento da (1) (con π=Λ, τ = 11, α = Λ, β = 11)
(3)    Λ → 1111   per transizione da (1) e (2)
 ...

Esempio 2:
Alfabeto: {A, B, C, (, ), *, o}.
Trovare Σ tale che si possano ottenere tutte le produzioni (x) → (y) con x parola contenente solo A, B o C e y parola inversa di x, e nessuna altra produzione del tipo (x) → (y) con x e y parole contenenti solo A, B o C.
Idea: uso * per effettuare inversioni di lettere e o per cancellare gli *.
In Σ metto:
( → (*       *AA → A*A       *AB → B*A     ...    *CB → B*C       *CC → C*C       *AC → C*A

in modo da poter ottenere:

(ABC)  →  (ABC) (ABC)  →  (*ABC) (*ABC)  →  (B*AC) (B*AC)  →  (BC*A) (BC*A)  →  (*BC*A) (*BC*A)  →  (C*B*A)

riflessività ( → (* e rimpiaz. *AB → B*A e rimp. *AC → C*A e rimp. ( → (* e rimpiaz. *BC → C*B e rimp.

e metto:    ( → (o    oA* → Ao    oB* → Bo    oC* → Co    oA) → A)    oB) → B)    oC) → C)

in modo da poter ottenere:

(C*B*A)  →  (oC*B*A)       (oC*B*A)  →  (CoB*A) (CoB*A)  →  (CBoA) (CBoA)  →  (CBA) (ABC)  →  (CBA)

... ... ... ... per transizione

   Non posso ottenere, ad es., la produzione (ABC)  →  (BAC) in quanto gli scambi li devo realizzare introducendo (a partire dall'inizio della parola) dei * che poi posso cancellare (facendo avanzare  o  fino davanti all'ultima lettera) solo se essi si alternano a lettere.

12. INDECIDIBILITÀ DEL CALCOLO DEI PREDICATI

   Riprendiamo il discorso avviato nella sezione 9.
   Sia P un TP-programma per il quale è indecidibile il problema dell'arresto.
(1)   Vogliamo tradurre la convergenza di P con input v in un problema di parole, che sarà quindi un problema di parole indecidibile.
(2)   Poi vedremo come tradurre i problemi di parole in formule del calcolo dei predicati. Da ciò dedurremo che il calcolo dei predicati è indecidibile.
   Affrontiamo (1).
   Come abbiamo già osservato conviene passare alla macchine di Turing. Sia M la macchina di Turing equivalente a P (vedi fine di sezione 10). Siano q₁, ..., q_n gli stati di M (cioè siano n    1 le istruzioni di P).

Idea: rappresentare le configurazioni illustrate nell'esempio della sezione 10 con le parole: hq₁111h, h1q₂11h, h1q₁01h, ... Usiamo il simbolo "h" delimitare la parte "attiva" del nastro (una porzione contenente il primo e l'ultimo "1"), come se indicasse una sequenza illimitata di "0". A destra del simbolo di stato compare il contenuto della cella osservata. Quindi usiamo, ad es., h10011q_i0h invece di h100110q_ih.
   Consideriamo l'alfabeto {0,1,q₁, ..., q_n,h} e Σ costituito:
per ogni quadrupla di M del tipo q_ixyq_j con x, y in {0,1} dalla produzione:
   q_ix → q_jy,
per ogni quadrupla di M del tipo q_ixDq_j con x in {0,1} dalle produzioni:
   q_ix0 → xq_j0, q_ix1 → xq_j1, q_ixh → xq_j0h
per ogni quadrupla di M del tipo q_ixSq_j con x in {0,1} dalle produzioni:
   0q_ix → q_j0x,1q_ix → q_j1x, hq_ix → hq_j0x

   Abbiamo tradotto in produzioni i comandi impartiti dalle quadruple. Per rappresentare l'arresto del programma (cioè il raggiungimento dell'ultimo stato q_n: così abbiamo tradotto lo stop passando dai TP-programmi alle TM), aggiungiamo a Σ:
   q_n0 → q_n, 0q_n → q_n, q_n1 → q_n, 1q_n → q_n
In questo modo l'arresto del programma, cioè arrivare a una parola che contiene q_n, corrisponde a ottenere la produzione della parola hq_nh.
   Dunque il problema di parole "Σ |— hq₁vh → hq_nh?" è risolubile sse P con input v si arresta.

   Abbiamo completato (1).    Affrontiamo (2):
RAPPRESENTAZIONE del problema "da Σ deriva α → β?" nel CALCOLO DEI PREDICATI

   Simbolo funzionale a due posti F (scriveremo +) per indicare la concatenazione di lettere, simbolo relazionale R a due posti per indicare le produzioni (scriveremo >), simboli di costanti per rappresentare le "lettere"
   L'associatività della concatenzazione è esprimibile con la formula:
A:   x+(y+z) = (x+y)+z
   Le regole di derivazione sono esprimibili con:
B:   x > x
C:   x > y & y > z  →  x > z
D:   x > y  →  z+x+w > z+y+w
   Per ogni produzione π → τ di Σ consideriamo una formula del tipo:
E:    π > τ
   Se Σ è costituito da n produzioni, avremo n formule E₁, ..., E_n di questo tipo.
   Il problema di parole è rappresentato dalla formula:
A & B & C & D & E₁ & ... & E_n  →  α > β
   Abbiamo che:
da Σ deriva α →  β sse
           A & B & C & D & E₁ &...& E_n  →  α > β è un teorema del calcolo dei predicati.
   Poiché esistono problemi di parole indecidibili, possiamo concludere che il calcolo dei predicati è indecidibile.