La natura della Matematica e i suoi rapporti con la Realtà:
inquadramento teorico e problemi didattici - Parte 1

Insegnamento astratto della matematica o riferito a contesti reali?

Tra gli argomenti a favore dell'inclusione di situazioni reali e di attività di modell(izz)azione nell'insegnamento della matematica si possono distinguere
• quelli che sottolineano come il riferimento alla realtà offra opportunità per la formazione culturale e sociale dei cittadini e
• quelli che mettono a fuoco le loro potenzialità nel favorire una costruzione profonda ed equilibrata dei concetti matematici.
  Qui affronteremo questioni legate a questi ultimi, anche perché sono di questo genere le argomentazioni di chi, al contrario, propende per un insegnamento con un approccio più "astratto".
  E sono di questo genere le argomentazioni che hanno condizionato, e continuano a condizionare, l'approccio all'educazione matematica che, specie nella scuola di base, parte dalla cosiddetta "insiemistica" … .  Per un approccio più "distaccato", partiremo da considerazioni riferite a questa fascia scolastica.

L'apprendimento: l'alunno e ...

Per molti anni lo studio e la realizzazione di curricoli e percorsi didattici sono state influenzate da riferimenti teorici secondo i quali la costruzione della conoscenza è considerata un processo personale, sollecitato dagli stimoli esterni e incanalato dai vincoli ambientali contingenti, ma fondamentalmente realizzato per opera dei meccanismi interni di adattamento:
• ricerche di tipo comportamentista (che privilegiavano lo studio di forme di apprendimento basate sulla acquisizione di abilità per risolvere problemi e sulla capacità di connettere più abilità per risolvere nuovi problemi più complessi),
• ricerche di psicologia dello sviluppo (volte a individuare tappe ed età per lo sviluppo delle capacità di ragionamento),
entrambe caratterizzate dallo studio sperimentale del comportamento di bambini in condizioni di "laboratorio".

Vediamo qualche esempio di questi studi, per discutere non tanto le loro tesi (sulle capacità di ragionamento e astrazione) e le ricadute negative che hanno avuto sull'impostazione dei curricoli matematici, quanto il modo in cui era esplorato il comportamento cognitivo e culturale di bambini e ragazzi, i cui limiti faremo emergere dal confronto con indagini svolte in anni successivi.

"Esperimento" 1 (prototipo di vari esperimenti fatti intorno al 1960):

Un plastico e un pupazzo. Al bambino viene chiesto di scegliere tra varie illustrazioni quella che rappresenta ciò che vede il pupazzo. La grande maggioranza dei bambini a 9 anni sbaglia e sotto ai 7 anni sceglie l'illustrazione che rappresenta il proprio punto di vista.

La figura a destra si riferisce a un nuovo esperimento (anni 70). Due pupazzi-poliziotti presso gli spigoli di una paratia a croce. Viene chiesto al bambino di porre un pupazzo-bambino in un posto in cui i poliziotti non lo possano vedere. I punti di vista da intersecare ora sono due. Tuttavia il 90% dei bambini di 4 anni risolve correttamente il problema.

Esperimenti volti allo stesso tipo di esplorazione. Perché questo cambiamento tra "esperimento" e "esperimento-bis"?

"Esperimento" 2 

Un bambino viene posto di fronte a sei oggetti dello stesso tipo, ad esempio a 6 gatti giocattolo, dei quali 4 neri e 2 bianchi.

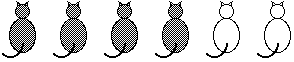
Davanti alla domanda "vi sono più gatti neri o più gatti?" solo il 25% dei bambini intorno ai 6 anni risponde correttamente, gli altri confrontano i gatti neri non con la totalità dei gatti, ma con i gatti bianchi.
BIS:  considerando gatti "seduti" e riformulando la domanda nel seguente modo: "vi sono più gatti neri o più gatti seduti?", la percentuale di risposte corrette passa da 25% a 50%.   Perché?

"Esperimento" 3 

(1)  Al bambino vengono fatte osservare due asticciole uguali collocate nel modo illustrato a lato.		———————— ————————
(2)  Gli viene chiesto se esse hanno la stessa lunghezza; il bambino, di norma, risponde affermativamente
(3)  Con frasi e con gesti si fa fissare la sua attenzione sul movimento che si sta per eseguire.
(4)  Si esegue la traslazione di una delle due asticciole nel modo illustrato a lato.		————————       ————————
(5)  Si ripropone la domanda se le due asticciole abbiano la stessa lunghezza; nella maggioranza dei casi a questo punto si ottiene una risposta negativa.

L'esperimento BIS consiste nella sostituzione delle fasi (3) e (4) con, ad esempio, l'intervento di un "pupazzo birichino" che cadendo sulle asticciole le sposta in modo casuale. Si ottiene in questo caso una grande maggioranza di risposte affermative alla domanda finale.  Perché?

[discussione]

Il cambiamento di comportamenti con i "secondi" esperimenti mette in luce che:
• il riferimento alla esperienze dei bambini (contesti familiari o di gioco in cui ci si pone il problema di nascondersi che vengono richiamati dall'esperimento bambino-poliziotti), facilita la comprensione del problema e ha un senso umano che stimola ad impegnarsi a risolverlo,
• apparenti problemi di ragionamento sono spesso invece di comunicazione: attraverso le fasi (3) e (4) dell'esperimento "asticciole" si crea nel bambino una tensione che lo porta a interpretare il successivo messaggio linguistico difformemente dalle intenzioni dello sperimentatore (il modo in cui è stato effettuato lo spostamento può indurre al confronto tra il posizionamento delle due asticciole lungo la direzione della "lunghezza" o al confronto tra lo spazio complessivamente occupato prima e dopo), e pure nel 2° esperimento il bambino viene indotto a intendere il quesito (nel modo per altro più naturale) come richiesta di paragonare una sottoclasse con l'altra,
• più in generale, il significato con cui è recepita un'attività didattica o un "esperimento" dipende anche da come questo interagisce con l'insieme delle esperienze, dei concetti e delle conoscenze di coloro a cui viene proposto (esperimento 1), e da che cosa questi "pensano che voglia" chi propone loro domande o attività (negli esperimenti 2 e 3 la tensione creata fa sì che il bambino si aspetti che la domanda, altrimenti banale, debba avere risposta negativa e ne interpreta quindi diversamente il significato).

L'apprendimento: linguaggi e conoscenze scolastiche e ...

La costruzione della conoscenza, dunque, dipende da complesse interazioni con esperienze e persone, di cui non è facile tener conto nei processi di insegnamento/valutazione. Ma, poniamoci un altro problema.

Pierino a 11 anni a scuola, di fronte al problema "standard" di compra-vendita «quanti pacchetti di figurine posso comprare con 50 centesimi se un pacchetto ne costa 15» non sa trovare una risposta in quanto si blocca di fronte al calcolo 0.50 : 0.15; però, fuori dalla scuola, sa che con 50 centesimi può comprare 3 pacchetti di figurine che costano 15 centesimi l'uno e che gli rimarrebbero 5 centesimi.

Non solo, di fronte alla domanda dell'insegnante, non riesce neanche a pensare a che cosa farebbe dal giornalaio e a utilizzare ciò per dare una risposta. Perché?

[discussione]

(1) «il territorio che abbiamo davanti ai nostri occhi è pianeggiante»
(2) «spero che oggi non faccia freddo come ieri»

Come farei ad esprimere (2) senza linguaggio?

– Se descrivo un incidente che ho avuto usando una gomma per la moto e due matite per le auto coinvolte riesco a rappresentare efficacemente la scena come non riuscirei mai solo a parole;
– l'interlocutore può muovere gli stessi oggetti per chiedere chiarimenti; ...
– ... anche se gli oggetti non rappresentano fedelmente dimensioni, masse, ... dei mezzi, anche se trascuro la rappresentazione di marciapiedi, case, ... .

• Il potere della mente umana in assenza di sussidi è piuttosto limitato.
• Questi sussidi sono artefatti cognitivi, ossia oggetti (la gomma, …) o costruzioni artificiali ad hoc (il linguaggio), che l'uomo usa come protesi della sua mente.
• Gli artefatti cognitivi sono strumenti. La loro efficacia dipende da come li usiamo. La gomma per chi non partecipa alla discussione dell'incidente non rappresenta una moto. Un libro se non so leggere, o se non sono in grado di riflettere su quello che sto leggendo, non funziona come artefatto cognitivo.
Due esempi "matematici":   tacche,   parti del corpo.

Un ruolo particolare hanno gli artefatti costruiti ad hoc, e in particolare quelli che si basano su segni grafici (lettere, cifre, diagrammi, …).
In una società a cultura orale l'istruzione formale ha un ruolo trascurabile: l'educazione avviene essenzialmente attraverso l'apprendistato, l'osservazione/imitazione.
Non esiste matematica (come disciplina), non esiste una storia "formale", ...

Ma la nostra scuola è sempre in grado di
• motivare e dare significato culturale agli strumenti di rappresentazione che introduce suscitando bisogni di riflessione/comunicazione come di fronte a una frase del tipo (2)?
• individuare il giusto grado di astrazione, come nel caso della descrizione dell'incidente, in cui l'interlocutore riesce a condividere percezioni, esperienze e pensieri, operando, senza sforzo, sulle loro rappresentazioni?
• mettere gli alunni in grado di scegliere le rappresentazioni più adatte (come gomma e matite) ad accompagnare i loro processi mentali, per trasformare un problema in un altro più facile da manipolare mentalmente
• o, almeno, far sì che gli artefatti siano percepiti come strumenti cognitivi, come "libri-libri", non come libri-cose"?

[Ripensiamo a Pierino]

La matematica

Le discipline (e altre forme organizzate di conoscenze) mettono a punto linguaggi, teorie, ...
• per facilitare la messa a punto e lo studio di una particolare classe di modelli, cioè di rappresentazioni astratte di oggetti o fenomeni "reali" (di tipo materiale: una rappresentazione topografica è il modello di un territorio; di tipo sociale: i concetti di "verbo", "sostantivo", ... sono dei modelli per rappresentare certi elementi della comunicazione verbale; ... o di tipo astratto: la "proprietà commutativa" è un modello per descrivere un aspetto di alcune operazioni matematiche),
• realizzate con artefatti materiali (segni grafici, carta quadrettata, ...) e con artefatti non materiali, che sono a loro volta modelli (il concetto di "parallelismo" che interviene nel modello "i raggi del sole arrivano paralleli", i concetti di "forza", "massa" e "accelerazione" per intervengono nel modello "secondo principio della meccanica" [F = m a], ...).

In genere una disciplina si occupa di modelli riferiti a una particolare area di problemi o di fenomeni:
ad esempio la fisica cerca di determinare i fattori e le condizioni che sono all’origine dei movimenti dei corpi, della trasmissione dei suoni e della luce, dei fenomeni elettrici, delle caratteristiche dei materiali,
e la linguistica cerca di individuare i principali meccanismi attraverso cui, nelle varie lingue, a partire dai suoni vengono formate le parole, le frasi, i discorsi.

La matematica ha la specificità di non essere caratterizzata da una particolare area fenomenologica, ma dalla tipologia degli artefatti che impiega per la costruzione dei modelli, per cui nel suo insegnamento
• i problemi individuati sopra assumono un rilievo maggiore,
• così come la gestione del passaggio da artefatti concreti ad artefatti man mano più astratti, o meglio, il dare concretezza (mentale e culturale), il rendere "realtà" artefatti man mano più lontani da forme elementari di percezione,
• e più in generale, la gestione dei rapporti tra contesti, concetti intuitivi, concetti disciplinari e rappresentazioni mentali degli alunni.

Suggerimento che sembra emergere: fare delle attività didattiche più vicine alla realtà.
Bene. Discutiamone alcune.

Difficoltà didattiche

(1) Per sviluppare il concetto di simmetria mostriamo agli alunni degli specchi e organizziamo una attività a partire da essi. In un secondo tempo, di fronte a esercizi del tipo: costruisci l'immagine speculare di A, B e C:

pochissimi sanno affrontare il caso C.

Perché? Che cosa faresti tu se fossi al posto di quest'insegnante? Eviteresti esercizi del tipo C in modo da non far nascere conflitti tra specchi "matematici" e specchi "fisici"? Spiegheresti come vanno risolti esercizi del genere e proporresti numerosi esercizi analoghi per far "assorbire" agli alunni il procedimento? ... [clicca]

(2) Quali misconcetti stanno dietro all'alunno che procede così? [clicca]

            *   * 
   (3x+3)(x-1-x+1)+4  (3x+3)+4  3x+3+4
          *   *

(3) (a) Come si scrivono "uno e tre" e "mille e tre"? È sbagliato scrivere 1.03 o 1300?
  (b) La popolazione della provincia di Genova è circa i 3/2 di quella del comune di Genova. È corretto dire la popolazione della provincia è una frazione di quella del comune?
  (c) Si può dire che i pezzi di tessuto A e B hanno un motivo uguale? E che le figure (1) e (2) sono uguali?
   
  (d) L'informazione che comunico quando dico "non arrivo a 39 di febbre" è tutta rappresentata dalla formula  T < 39  dove con T indico la mia temperatura corporea in gradi Celsius?

[discussione]