Antiderivatives

Let f(x) be continuous on [a,b]. If G(x) is continuous on [a,b] and G´(x) = f(x) for all x ∈ (a,b), then G is called an antiderivative of f.

We can construct antiderivatives by integrating. The function

F(x) = ⌠
⌡		 x

a 
 f(t) dt
is an antiderivative for f since it can be shown (see Fundamental Theorem of Calculus) that F(x) constructed in this way is continuous on [a,b] and F´(x) = f(x) for all x ∈ (a,b).

Properties

Let F(x) be any antiderivative for f(x).

  • For any constant C, F(x)+C is an antiderivative for f(x).

    proof:

    Since d
    dx    		 [F(x)] = f(x),

    d
    dx
    		 [ F(x)+C ]
    =
    d
    dx
    		 [ F(x) ]+ d
    dx
    		 [C]
    =
    f(x)+0
    =
    f(x)
    so F(x)+C is an antiderivative for f(x).

  • Every antiderivative of f(x) can be written in the form
    F(x)+C
    for some C. That is, every two antiderivatives of f differ by at most a constant.

    proof:

    Let F(x) and G(x) be antiderivatives of f(x). Then F´(x) = G´(x) = f(x), so F(x) and G(x) differ by at most a constant (this requires proof---it is shown in most calculus texts and is a consequence of the Mean Value Theorem).

The process of finding antiderivatives is called antidifferentiation or integration.

∫f(x) dx is called the indefinte integral of f(x).  It is used to denote:
• a generic term F(x) where F is an antiderivative of f, or
• the set of the terms F(x)+C (C real number) where F is an antiderivative of f, i.e. all the terms T such that Dx(T) = f(x).
    È lasciata al lettore l'interpretazione della notazione a seconda del contesto (l'ambiguità di questa notazione, l'uso di un "+C" come nelle espressioni seguenti, per evidenziare che, data una primitiva, se ad essa aggiungo comunque una costante ottengo un'altra primitiva, sono brutte convenzioni entrate nell'uso in tempi antichi che, "per pigrizia", sono state mantenute; anche qui se ne fa uso, per abituare il lettore ad esercitare le opportune "interpretazioni").
d
dx
 [F(x)] = f(x)
       ⇔
       ⌠
⌡		 f(x) dx = F(x)+C.
d
dx
 [g(x)] = g´(x)
       ⇔
       ⌠
⌡		 g´(x) dx = g(x)+C.

Properties of the Indefinite Integral

 d
dx		 [∫ f(x) dx] = f(x)
i.e.:  Dx(F(x)+C) = f(x) for all C if F is an antiderivative of f

  • (Linearity) ∫[αf(x)+βg(x)] dx = α∫ f(x) dx+β∫ g(x) dx.
    i.e.: "the set of all antiderivates of αf+βg is equal to the set of the functions αF+βG such that F is an antiderivative of f and G is an antiderivative of g"
    i.e.:  ∫αf(x)+βg(x) dx = αF(x)+βG(x)+C  if  ∫f(x)dx = F(x)+C  and  ∫g(x)dx = G(x)+C.

    proof:

    We need only show that α∫ f(x) dx+β∫g(x) dx is an antiderivative of αf(x)+βg(x):

    d
    dx
    		 /
    | 
    \    		 α⌠
    ⌡    		 f(x) dx+β⌠
    ⌡    		 g(x) dx\
     |
    /
    =
    α d
    dx
    		 /
    | 
    \    		⌠
    ⌡    		 f(x) dx\
     |
    /    		 +β d
    dx
    		 /
    | 
    \    		⌠
    ⌡    		 g(x) dx\
     |
    /
    =
    αf(x)+βg(x).

Examples

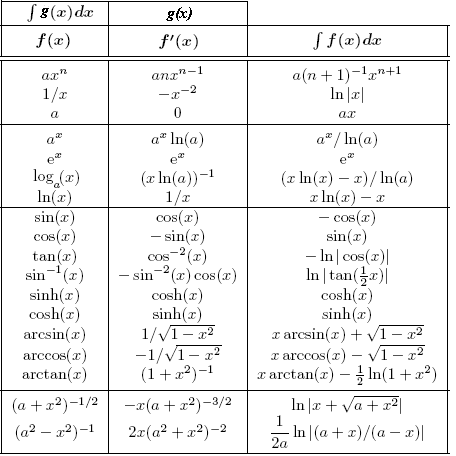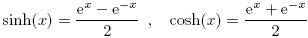
  1. Every antiderivative of x2 has the form x3/ 3 + C, since d/dx[x3/ 3] = x2.
  2. d/dx[∫ x5 dx] = x5.

Nota. La scrittura ∫(1/x)dx = log|x| (+c), spesso usata (come nella tabella riprodotta sopra), non è, a rigore, corretta: le antiderivate (rispetto a x) di 1/x non hanno la forma log|x|+c, ossia non è vero che per ogni antiderivata f(x) di 1/x esiste c tale che f(x) = log(x)+c per x>0 e f(x) = log(-x)+c per x<0, ma esistono c1 e c2 tali che f(x) = log(x)+c1 per x>0 e f(x) = log(-x)+c2 per x<0; infatti il dominio della funzione continua 1/x non è un intervallo, ma l'unione di due intervalli:  esercizio e soluzione.

Key Concepts [index]

If G(x) is continuous on [a,b] and G´(x) = f(x) for all x ∈ (a,b), then G is called an antiderivative of f.

We can construct antiderivatives by integrating. The function

F(x) = ⌠
⌡		 x

a 
 f(t) dt
is an antiderivative for f. In fact, every antiderivative of f(x) can be written in the form F(x)+C, for some C.

d
dx
 [F(x)] = f(x)
       ⇔
       ⌠
⌡		 f(x) dx = F(x)+C.
d
dx
 [g(x)] = g´(x)
       ⇔
       ⌠
⌡		 g´(x) dx = g(x)+C.