Arc Length

Suppose f is continuously differentiable on the interval [a,b].

Let's derive a formula for the length L of the curve on the interval, called the arc length over [a,b].

We'll start by subdividing the interval [a,b] into n subintervals [x0, x1], [x1, x2], ... , [xn-1,xn] where a = x0 < x1 < … < xn-1 < xn = b.

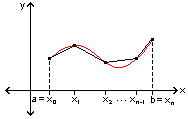
Introduce the line segments between (x0, f(x0)) and (x1,f(x1)), (x1, f(x1)) and (x2, f(x2)), ..., (xn-1, f(xn-1)) and (xn, f(xn)).

The resulting polygonal path approximates the curve given by y = f(x), and its length approximates the arc length of f(x) over [a,b].


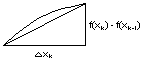
Let's find the length of the polygonal path by adding up the lengths of the individual line segments. The kth line segment is the hypotenuse of a triangle with base Δxk and height f(xk)-f(xk-1) and so has length


Lk = 		   ___________________
√ (Δxk)2+[f(xk)-f(xk-1)]2.

By the Mean Value Theorem there exists xk* ∈ [xk-1,xk] such that

f(xk)-f(xk-1)
xk-xk-1
 = f ′(xk*)

so

f(xk)-f(xk-1) = f ′(xk*)(xk-xk-1) = f ′(xk*)Δxk.

Thus,


Lk = 		   _________________
√ (Δxk)2+[f ′(xk*)Δxk]2
 =  		   __________
√ 1+[f ′(xk*)]2
Δxk.

Finally, the length of the entire polygonal path is

n
Σ
k = 1 
Lk = 		n
Σ
k = 1 
    __________
√ 1+[f ′(xk*)]2
Δxk
which has the form of a Riemann sum. Increasing the number of subintervals such that max Δxk → 0, the summation Σ kn= 1 Lk → L.

That is,

L   =
 lim
 max Δxk → 0 
 n
Σ
k = 1 
    __________
√ 1+[f ′(xk*)]2
Δxk
=
⌠
⌡		 b

a 
    __________
√ 1+[f ′(xk*)]2
dx
by the definition of the definite integral as a limit of Riemann sums. Thus, we have proved the following:

Arc Length

Let f(x) be continuously differentiable on [a,b]. Then the arc length L of f(x) over [a,b] is given by

L = ⌠
⌡		 b

a 
    _________
√ 1+[f ′(x)]2
dx

Similarly, if x = g(y) with g continuously differentiable on [c,d], then the arc length L of g(y) over [c,d] is given by

L = ⌠
⌡		 d

c 
    _________
√ 1+[g ′(y)]2
dy

These integrals often can only be computed using numerical methods.

Example

We can compute the arc length of the graph of f(x) = x3/2 over [0,1] as follows:

L   =
⌠
⌡		 1

0 
    _________
√ 1+[f ′(x)]2
dx
=
⌠
⌡		 1

0 
    ___________
√ 1+[3x1/2/2]2
dx
=
⌠
⌡		 1

0 
    _______
√ 1+9x/4
dx
=
8
27
 (1+9x/4)3/2 |
|
|		 1

0 
= (1+9/4)3/2-(1)3/2
= (13/4)3/2-1
≈ 1.44.

Key Concepts [index]

Let f(x) be continuously differentiable on [a,b]. Then the arc length L of f(x) over [a,b] is given by

L = ⌠
⌡		 b

a 
    _________
√ 1+[f ′(x)]2
dx

Similarly, if x = g(y) with g continuously differentiable on [c,d], then the arc length L of g(y) over [c,d] is given by

L = ⌠
⌡		 d

c 
    _________
√ 1+[g ′(y)]2
dy