Per spiegare perché, cambiando i versori mediante la trasformazione geometrica descritta da una matrice M, il cambiamento nelle nuove coordinate è descritto dalla matrice inversa di M può essere utile riflettere a ciò che accade in casi più semplici.

Data la curva A1 y=f(x), la curva A2 y-k = f(x-h) (ossia y = f(x-h)+k) è traslata orizzontalmente di h e verticalmente di k.
   
Se prendo come nuovo sistema di riferimento X,Y quello con origine in (h,k) e stesse scale sugli assi, la curva A2 posso descriverla come Y = f(X).
In pratica, avendo traslato gli assi di (h,k) le coordinate originali rispetto a quelle nelle nuove coordinate le ottengo aggiungendo rispettivamente h e k:
x = X+h, y = Y+k;  e quindi X = x-h, Y = y-k
Nel caso raffigurato y = (x-2)2-1 con X=x-2 (x=X+2) e Y=y+1 (y=Y-1) diventa Y = X2.
In altre parole, rispetto alle nuove coordinate la curva A2 assume l'equazione che avrebbe facendole fare la trasformazione geometrica opposta a quella che ha portato i versori dei vecchi assi (vedi segmenti evidenziati in verde scuro) in quelli dei nuovi (vedi i segmenti evidenziati in rosso).
   Analogamente data la curva B1 y = g(x), la curva B2 y = g(x/3) subisce una trasformazione di scala orizzontale di fattore 3.
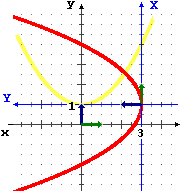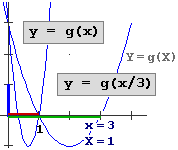
Se prendo come nuovo sistema di riferimento X,Y quello con stessa origine ma scala orizzontale tale che x=3 diventi X=1, ossia con segmento unitario con lunghezza fisica tripla rispetto a prima, la curva B2 posso descriverla come Y = g(X).
Dalle nuove coordinate ritorno alle vecchie con x = 3X, e viceversa con X 0 x/3; le ordinate non mutano: Y=y.
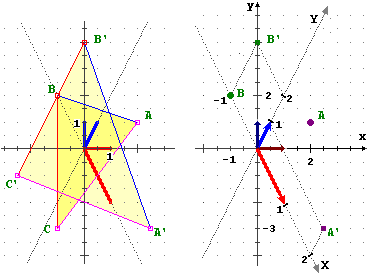
Anche in questo caso, rispetto alle nuove coordinate la curva ha assunto l'equazione che avrebbe facendole fare la trasformazione geometrica opposta a quella che ha portato i vecchi versori degli assi nei nuovi (il versore dell'asse y, evidenziato in blu, è rimasto uguale, quello dell'asse x è stato moltiplicato per 3: il segmento evidenziato in rosso è stato trasformato in quello evidenziato in verde).

L'ellisse  ((x-2)/2)2 + (y+3)2 = 1  è ottenuta con le trasformazioni  (x,y) → (2x,y)  e  (x,y) → (x+2,y-3)  dal cerchio  x2 + y2 = 1.
Nel nuovo sistema di riferimento X,Y con i versori ottenuti con la stessa trasformazione, l'ellisse diventa  X2 + Y2 = 1.
Il punto (0,-3) passando nel nuovo sistema diventa (-1,0), mediante le trasformazioni  (x,y) → (x-2,y+3)  - che lo trasla in (-2,0) -  e  (x,y) → (x/2,y)  - che lo scala in (-1,0). 		 

Nel caso della curva 3x+y2-2y-8 = 0 sotto tracciata in rosso voglio rappresentarla nel nuovo sistema di riferimento X,Y con origine (3,1) e assi ruotati di 90° rispetto al sistema x,y.
 
La trasformazione geometrica che hanno subito i versori degli assi è composta da una rotazione di 90°: x' = -y, y'= x  seguita dalla traslazione (3,1), per cui la trasformazione complessiva è: x' = -y+3, y'= x+1.
Quindi le coordinate originali x,y rispetto alla nuove X,Y le ritrovo applicando queste trasformazioni:
x = -Y+3, y = X+1.
Dunque 3x+y2-2y-8 = 0 diventa 3(-Y+3)+(X+1)2-2(X+1)-8 = 0, ossia -3Y+X2=0, ossia Y=X2/3.
In questo modo abbiamo scoperto che la nostra parabola è stata ottenuta con una rotazione di 90° e una traslazione di vettore (3,1) da y=x2/3.

Sotto a sinistra è raffigurato un triangolo e il suo trasformato mediante la trasformazione:
/x'\ = / 1 1/2\ × /x\ = /x + y/2\
\y'/   \-2  1 /   \y/   \-2x + y/
Sono evidenziati anche i trasformati dei versori, che diventano i vettori applicati in (0,0) con "punte" in:
/ 1 1/2\ × /1\ = / 1\   / 1 1/2\ × /0\ = /1/2\
\-2  1 /   \0/   \-2/   \-2  1 /   \1/   \ 1 /
In pratica sono le colonne della matrice M di trasformazione.
 
La figura sopra a destra illustra che se prendo come nuovo sitema di riferimento X,Y quello che ha questi come nuovi versori, i vertici del triangolo assumono come coordinate quelle che il vecchio triangolo aveva nel sistema di riferimento originale (ad es. A che aveva x=2, y=1 viene trasformato in A' con x=2.5, y=-3, ma che nel nuovo sistema ha X=2, Y=1). Ed è ovvio che sia così.
Più in generale un punto (X,Y) nel nuovo sistema ha coordinate nel vecchio che sarebbero quelle del trasformato di (x,y) mediante M:
/x\ = / 1 1/2\ × /X\ = M × /X\
\y/   \-2  1 /   \Y/       \Y/
Viceversa, per trovare le coordinate nel nuovo sistema del punto che nel vecchio ha coordinare (x,y) si può fare:
/X\ = M–1 × /x\
\Y/         \y/
Se si vogliono fare prove di trasformazione con Poligon si può tracciare una figura, definire una matrice A 2×2 e poi azionare:
plot x:=a[1,1]*x+a[1,2]*y y:=a[2,1]*x+a[2,2]*y
Se copi le seguenti righe e in Poligon azioni [CLP] vengono tracciati un pentagono regolare, i versori degli assi (in colori diversi) e i loro trasformati mediante la stessa matrice dell'esempio visto sopra:
N
p5
plot x:s y:14
plot x:0 y:0
plot x:1 y:0
plot x:s y:11
plot x:0 y:0
plot x:0 y:1
A[](2,2)=1,1/2,-2,1
plot x:=a[1,1]*x+a[1,2]*y y:=a[2,1]*x+a[2,2]*y
pp
+

Quasi ogni tipo di trasformazione geometrica è realizzabile con R (vedi).