The Chain Rule

You probably remember the derivatives of sin(x), x8, and ex. But what about functions like sin(2x-1), (3x2-4x+1)8, or e-x2? How do we take the derivative of compositions of functions?

The Chain Rule allows us to use our knowledge of the derivatives of functions f(x) and g(x) to find the derivative of the composition f(g(x)):

Suppose a function g(x) is differentiable at x and f(x) is differentiable at g(x). Then the composition f(g(x)) is differentiable at x.

Letting y = f(g(x)) and u = g(x),

dy
dx
 = dy
du
 · du
dx
 .
Using alternative notation,
d
dx
 [ f(g(x)) ]
=
f ′(g(x))g ′(x);
d
dx
 [ f(u) ]
=
f ′(u) du
dx
 ;
(f(g(.))' = f'(g(.))g'(.).

Proof

The four formulations of the Chain Rule given here are identical in meaning. In words, the derivative of f(g(x)) is the derivative of f, evaluated at g(x), multiplied by the derivative of g(x).

Examples

  • To differentiate sin(2x-1), we identify u = 2x-1. Then

    d
    dx
    		 [ sin(2x-1)]
    =
    d
    du
    		 [ sin (u) ] · d
    dx
    		 [ 2x-1 ]
    =
    cos(u) ·2
    =
    2 cos(2x-1).
    f(x)
    =
    sin(x)
    g(x)
    =
    2x-1
    f(g(x))
    =
    sin(2x-1)

  • To differentiate ( 3x2 - 4x + 1 )8, we identify u = 3x2-4x+1. Then

    d
    dx
    		 [( 3x2 - 4x + 1 )8]
    =
    d
    du
    		 [ u8 ] · d
    dx
    		 [ 3x2-4x+1]
    =
    8u7 ·(6x-4)
    =
    8 (6x-4)( 3x2 - 4x + 1 )7.
    f(x)
    =
    x8
    g(x)
    =
    3x2 - 4x + 1
    f(g(x))
    =
    ( 3x2 - 4x + 1 )8

  • To diffferentiate e-x2, we identify u = -x2. Then

    d
    dx
    		 [ e-x2 ]
    =
    d
    du
    		 [ eu] · d
    dx
    		 [ -x2 ]
    =
    eu ·(-2x)
    =
    -2xe-x2.
    f(x)
    =
    ex
    g(x)
    =
    -x2
    f(g(x))
    =
    e-x2

Sometimes you will need to apply the Chain Rule several times in order to differentiate a function.

Example

We will differentiate √
sin2 (3x) + x
 
.

d
dx
 /
| 
\		 √
sin2 (3x) + x
 
 \
 |
/
=
/
| 
| 
| 
\		 1
2√
sin2 (3x) + x
 
\
 |
 |
 |
/		 · d
dx
 [ sin2 (3x) + x]
f(u) = √u
=
/
| 
| 
| 
\		 1
2√
sin2 (3x) + x
 
\
 |
 |
 |
/		 · /
| 
\		 2 sin(3x) d
dx
 [ sin(3x) ] + 1 \
 |
/
f(u)
=
u2
d
dx
 [x]
=
1
=
/
| 
| 
| 
\		 1
2√
sin2 (3x) + x
 
\
 |
 |
 |
/		 · /
| 
\		 2 sin(3x)cos(3x) d
dx
 [3x] + 1 \
 |
/
f(u) = sin(u)
=
/
| 
| 
| 
\		 1
2√
sin2 (3x) + x
 
\
 |
 |
 |
/		 ·( 2 sin(3x)cos(3x) ·3 + 1 )
=
6 sin(3x) cos(3x) + 1
2√
sin2 (3x) + x
 

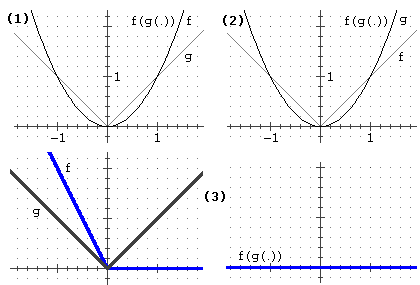
Nota.  f(g(.)) può essere derivabile in a senza che g sia derivabile in a o che f sia derivabile in g(a). La chain rule è  "suppose … then …",  non  "… if and only if …".
Esempi 
(1) f: x → x2, g: x → |x|, f(g(x)) = |x|2 = x2, a = 0 (g non è derivabile in a);
(2) f: x → |x|, g: x → x2, f(g(x)) = |x2| = x2, a = 0 (f non è derivabile in g(a) = 0);
(3) f: x → −x+|x|, g: x → |x|, f(g(x)) = −|x|+|x| = 0, a = 0 (g non è derivabile in a, f non è derivabile in g(a) = 0).
       

Key Concepts [index]

Let g(x) be differentiable at x and f(x) be differentiable at f(g(x)). Then, if y = f(g(x)) and u = g(x),

dy
dx
 = dy
du
 · du
dx
 .