Change of Basis

Let V be a vector space and let S = {v1,v2, …, vn} be a set of vectors in V. Recall that S forms a basis for V if the following two conditions hold:

  1. S is linearly independent.

  2. S spans V.

If S = {v1,v2, …, vn} is a basis for V, then every vector v ∈ V can be expressed uniquely as a linear combination of v1,v2, …, vn:
v = c1v1 + c2v2 + …+ cnvn.
Think of  /
| 
| 
| 
| 
| 
\
c1
c2
:
cn
 \
 |
 |
 |
 |
 |
/
as the coordinates of v relative to the basis S. If V has dimension n, then every set of n linearly independent vectors in V forms a basis for V. In every application, we have a choice as to what basis we use. In this tutorial, we will describe the transformation of coordinates of vectors under a change of basis.

We will focus on vectors in R2, although all of this generalizes to Rn. The standard basis in R2 is {[1 0]T,[0 1]T}. We specify other bases with reference to this rectangular coordinate system.

Let B = {u,w} and B ′ = {u ′,w ′} be two bases for R2. For a vector v ∈ V, given its coordinates [v]B in basis B we would like to be able to express v in terms of its coordinates [v]B ′ in basis B ′, and vice versa.

Suppose the basis vectors u ′ and w ′ fo B ′ have the following coordinates relative to the basis B:

[ u ′ ]B
=
/
| 
\
a
b
\
 |
/
[ w ′ ]B
=
/
| 
\
c
d
\
 |
/		 .
This means that
u ′
=
au + bw
w ′
=
cu + dw

The change of coordinates matrix from B ′ to B
P = /
| 
\
a
c
b
d
\
 |
/

governs the change of coordinates of v ∈ V under the change of basis from B ′ to B:
[v]B = P[v]B ′ = /
| 
\
a
c
b
d
\
 |
/		 [v]B ′.
That is, if we know the coordinates of v relative to the basis B ′, multiplying this vector by the change of coordinates matrix gives us the coordinates of v relative to the basis B.
P viene chiamata anche matrice di transizione dalle nuove coordinate a quelle iniziali.

Why?

The transition matrix P is invertible. In fact, if P is the change of coordinates matrix from B ′ to B, then P-1 is the change of coordinates matrix from B to B ′:

[v]B ′ = P-1[v]B

Example

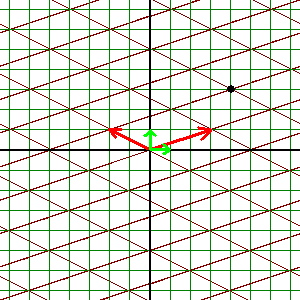
Let B = {[1 0]T,[0 1]T} and B ′ = {[3 1]T,[-2 1]T}. The change of basis matrix from B ′ to B is

P = /
| 
\
3
-2
1
1
 \
 |
/		 .
The vector v with coordinates [v]B ′ = [2 1]T relative to the basis B ′ has coordinates
[v]B = /
| 
\
3
-2
1
1
 \
 |
/		 /
| 
\
2
1
 \
 |
/		 = /
| 
\
4
3
 \
 |
/
relative to the basis B. Since
P-1 = /
| 
\
1/5
2/5
-1/5
3/5
 \
 |
/		 ,
we can verify that
[v]B ′ = /
| 
\
1/5
2/5
-1/5
3/5
 \
 |
/		 /
| 
\
4
3
 \
 |
/		 = /
| 
\
2
1
 \
 |
/
which is what we started with.

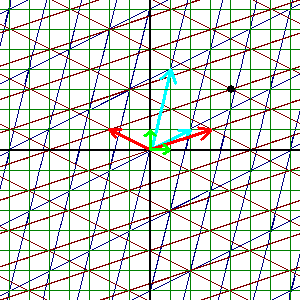
In the following example, we introduce a third basis to look at the relationship between two non-standard bases.

Example

Let B ′ ′ = { /
| 
\		 2
1
 \
 |
/		 ,  /
| 
\		 1
4
 \
 |
/		 } .
To find the change of coordinates matrix from the basis B ′ of the previous example to B ′ ′, we first express the basis vectors

/
| 
\		 3
1
 \
 |
/
and
/
| 
\		 -2
1
 \
 |
/
of B ′ as linear combinations of the basis vectors
/
| 
\		 2
1
 \
 |
/
 and
/
| 
\		 1
4
 \
 |
/
of B ′ ′:

/
| 
\
3
1
 \
 |
/
=
11
7
 /
| 
\
2
1
 \
 |
/		 −  1
7
 /
| 
\
1
4
 \
 |
/
/
| 
\
-2
1
 \
 |
/
=
-9
7
 /
| 
\
2
1
 \
 |
/		 +  4
7
 /
| 
\
1
4
 \
 |
/
      
Set /
| 
\
3
1
 \
 |
/
=
a /
| 
\
2
1
 \
 |
/		 + b /
| 
\
1
4
 \
 |
/
/
| 
\
-2
1
 \
 |
/
=
c /
| 
\
2
1
 \
 |
/		 + d /
| 
\
1
4
 \
 |
/
and solve the resulting systems for a,b,c, and d.

Thus, the transition matrix from B ′ to B ′ ′ is

/
| 
| 
| 
| 
| 
\
11
7
-9
7
-1
7
4
7
\
 |
 |
 |
 |
 |
/		 .
The vector v with coordinates [2 1]T relative to the basis B ′ has coordinates
/
| 
| 
| 
| 
| 
\
11
7
-9
7
-1
7
4
7
\
 |
 |
 |
 |
 |
/		 /
| 
\
2
1
 \
 |
/		 = /
| 
| 
| 
| 
| 
\
13
7
2
7
\
 |
 |
 |
 |
 |
/
relative to the basis B ′ ′. This is, back in the standard basis,
[ v ]B = 13
7
 /
| 
\
2
1
 \
 |
/		 + 2
7
 /
| 
\
1
4
 \
 |
/		 = /
| 
\
4
3
 \
 |
/		 ,
which agrees with the results of the previous example.

Rotation of the Coordinate Axes

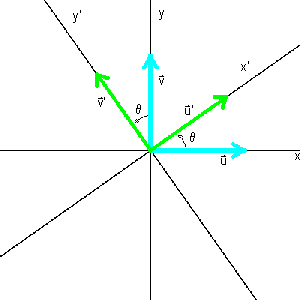
Suppose we obtain a new coordinate system from the standard rectangular coordinate system by rotating the axes counterclockwise by an angle θ. The new basis B ′ = {u ′, v ′} of unit vectors along the x ′- and y ′-axes, respectively, has coordinates

[u ′]B
=
/
| 
\
cosθ
sinθ
 \
 |
/
[v ′]B
=
/
| 
\
-sinθ
cosθ
 \
 |
/
in the original coordinate system. Thus,
P = /
| 
\
cosθ
 
-sinθ
sinθ
cosθ
 \
 |
/		  and P-1 = /
| 
\
cosθ
sinθ
-sinθ
cosθ
 \
 |
/
A vector [x y]TB in the original coordinate system has coordinates [x ′ y ′]TB ′ given by
/
| 
\
x ′
y ′
 \
 |
/

B ′ 
 = /
| 
\
cosθ
sinθ
-sinθ
cosθ
 \
 |
/		 /
| 
\
x
y
 \
 |
/

B 
in the rotated coordinate system.

Example

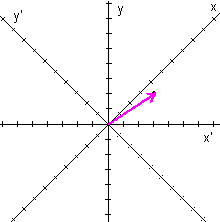
The vector [v]B = [3 2]T in the original coordinate system has coordinates

[v]B ′ = /
| 
| 
| 
| 
| 
\
√2
2
√2
2
- √2
2
√2
2
\
 |
 |
 |
 |
 |
/		 /
| 
\
3
2
 \
 |
/		 = /
| 
| 
| 
| 
| 
\
5√2
2
- √2
2
\
 |
 |
 |
 |
 |
/
in the coordinate system formed by rotating the axes by 45°.

Note.
• Nel caso di una semplice rotazione degli assi si può osservare che P-1=Pt, ossia che l'inversa della matrice di transizione si può trovare semplicemente scambiando righe con colonne.
Una matrice A tale che A-1= At (ovvero A×At=I) si dice ortogonale.
[dato che det(At)=det(A) e det(A-1)=1/det(A), si ha che det(A)=±1]
Si può dimostrare che ogni cambiamento di base in cui la nuova base e1,e2 sia ortonormale (o cartesiana o euclidea), ossia formata da vettori tra loro perpendicolari e di modulo 1 (ossia tali che ei·ej = 1 se i=j, ei·ej = 0 altrimenti) è descritto da una matrice di transizione ortogonale (e viceversa: se la matrice di transizione è ortogonale, da una base cartesiana si ottiene un'altra base cartesiana).
• Nel caso di R3 la rotazione degli assi è caratterizzata dagli angoli formati da ogni nuovo asse col corrispondente vecchio (vedi Geometria delle trasformazioni lineari).
Nel caso di R2 P ha come prima colonna cos(θ),sin(θ) che equivale a cos(θ),cos(φ) (le proiezioni del versore di x' sui vecchi assi) dove θ e φ (= π/2-θ) sono gli angoli che x' forma con x e con y; e come seconda colonna -sin(θ),cos(θ) che equivale a cos(ψ),cos(θ), dove ψ (=π/2+θ) e θ sono gli angoli che y' forma con x e y. P-1 ha come elemento di posto (i,j) cos(x'i, xj), avendo indicato i due assi con x1,x2.
Lo stesso accade per R3, dove x1,x2,x3 stanno per x,y,z (P è la matrice A considerata alla fine di Geometria delle trasformazioni lineari; P-1, per quanto osservato nella prima Nota, è la trasposta di A).

Key Concepts [index]

Let B = {u,v} and B ′ = { u ′, v ′ } be two bases for R2. If [u]B = [a b]T and [v]B = [c d]T, then

P = /
| 
\
a
c
b
d
 \
 |
/
is the change of coordinates matrix from B ′ to B and P-1 is the change of coordinates matrix from B to B ′. That is, for any v ∈ V,

[v]B
=
P[v]B ′
[v]B ′
=
P-1[v]B.