In this tutorial, we review some of the most common tests for the convergence of an infinite series

Let

∞ ∑ k = 0  ak = L.

For j ≥ 0, ∞ ∑ k = 0 ak converges if and only if ∞ ∑ k = j ak converges, so in discussing convergence we often just write ∑ak.

Example

Consider the geometric series

It is easy to see that

∞ ∑ k = 0

xk diverges for |x| ≥ 1.

Thus

∞ ∑ k = 0

xk = 1/(1-x) for |x| < 1 and diverges for |x| ≥ 1.

Example
∑_k=1..∞1/k = 1 + 1/2 + 1/3 + 1/4 + ... (serie armonica) diverge, infatti:
1 + (1/2 + 1/3 + ... + 1/10) + (1/11 + ... + 1/100) + (1/101 + ... + 1/1000) + ... >
1 + (1/10 + 1/10 + ... + 1/10) + (1/100 + ... + 1/100) + (1/1000 + ... + 1/1000) + ... =
1 + 9·1/10 + 90·1/100 + 900·1/1000 + ... = 1 + 0.9 + 0.9 + 0.9 + ...
A questo punto, se ci è chiaro il concetto di convergenza di una serie, ci appare ovvia la divergenza della nostra serie. Dimostriamolo, comunque, usando la formalizzazione del concetto.
    Consideriamo la nª somma parziale con n eguale a una potenza di 10: n = 10^h.
a(h) = s_10^h = ∑_k=1..n 1/k > 1 + (1/10 + 1/10 + ... + 1/10) +...+ (1/10^h + ... + 1/10^h) = 1 + 0.9h → ∞ per h → ∞
La successione a(h) non converge; essa è costituita dagli elementi di posto eguale a una potenza di 10 della successione s_n, quindi neanche questa può convergere (se convergesse a L, comunque fissassi ε potrei trovare n tale che tutte le s_n con n > n distino da L meno di ε, e questo dovrebbe accadere anche per tutte le potenze di 10 maggiori di n).

Divergence Test

Example

The series

∞ ∑ k = 0

k/(2k+1) diverges, since

lim k → ∞

k/(2k+1) = 1/2 ≠ 0.

Nota.  L'esempio della serie armonica mette in luce che la convergenza a 0 (per k → ∞) del termine a(k) è condizione necessaria ma non sufficiente per la convergenza della serie.

Integral Test

---

Let f(x) be continuous, decreasing, and positive for x ≥ 1.

Then

∞ ∑ k = 1

f(k) converges if and only if ∫

∞ 1

f(x)dx converges.

Example

Consider the p-series ∞ ∑ k = 1  1 kp = 1 1p + 1 2p + 1 3p + … Since ∫ ∞ 1  1 xp dx = 1 1-p x1-p | | | | ∞ 1  ,    p > 1 ln|x| |1∞ ,    p = 1 1 1-p x1-p | | | | ∞ 1  ,    0 < p < 1 = 1 1-p ∞ ∞, the series converges for p > 1 and diverges for 0 < p ≤ 1.

The divergent p-series ∞ ∑ k = 1  1 k with p = 1 is called the Harmonic Series. [la cui divergenza era già stata dimostrata sopra con tecniche più elementari]

Comparison Test

1. If ∑b_k converges, then ∑a_k also converges.

2. If ∑a_k diverges, then ∑b_k also diverges.

Informally, if the ``larger'' series converges, so does the ``smaller.'' If the ``smaller'' series diverges, so does the ``larger.''

Examples

•  Since ∞ ∑ k = 1 1/(k2) converges, so does ∞ ∑ k = 1 1/(k2 + 3).

1/(k2 +3) < 1/(k2) for all k

•  Since ∞ ∑ k = 1 1/k diverges, so does ∞ ∑ k = 1 1/(ln|k+1|).

1/(ln|k+1|) > 1/k for k ≥ 2

Limit Comparison Test

Example

The series

∞ ∑ k = 1

(k2-1)/( 5k3) diverges, since

∞ ∑ k = 1

1/k diverges and

Ratio Test   (D'Alembert's test)

1. If L < 1, then ∑a_k converges.

2. If L > 1, then ∑a_k diverges.

3. If L = 1, then the test is inconclusive.

Example

The series

∞ ∑ k = 1

1/k! converges, since

Root Test

1. If L < 1, then ∑a_k converges.

2. If L > 1, then ∑a_k diverges.

3. If L = 1, then the test is inconclusive.

Example

The series

∞ ∑ k = 0

[k/( 2k+1)]k converges, since

Alternating Series Test   (Leibniz's test)

If ak+1 < ak for all k and lim ak = 0, then

∞ ∑ k = 0

(-1)kak converges

Example

1 - 1/2 + 1/3 - 1/4 + 1/5 - ... 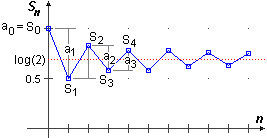   grafico della somma parziale Sn in funzione di n Sn = a0- a1+ ... + (-1)n an Essendo an decrescente la somma S [che si può dimostrare in questo caso essere uguale a log(2)] è approssimata per eccesso da S0, S2, … e per difetto da S1, S3, … Sn "oscilla" attorno a S con oscillazione che si smorza. L'errore che si commette approssimando S con Sn ha valore assoluto minore di an+1.

∞ ∑ k = 0

(-1)k (k+1)

converges, since 1/((k+1) + 1) < 1/(k+1) and

lim k → ∞

1/(k+1) = 0.

This series is conditionally convergent, rather than absolutely convergent, since

∞ ∑ k = 0

| ((-1)k)/(k+1) | =

∞ ∑ k = 0

1/(k+1)

diverges.

NOTA 1.
Evidentemente, se una serie converge assolutamente (∑ |a_n|<∞) allora converge (esiste S numero reale t.c. S = ∑ a_n).
Infatti siano b_n la successione ottenuta da a_n azzerando i termini negativi e c_n quella ottenuta azzerando quelli positivi, in modo tale che a₁+ ... +a_n = (b₁+c₁) + ... + (b_n+c_n) = (b₁+ ... +b_n) + (c₁+ ... +c_n) con b_i e -c_i tutti non negativi.
Da ∑ |a_n|<∞ segue (per il citerio del confronto) che si ha anche ∑ b_n<∞ e ∑ (-c_n)<∞. ∑ c_n = -∑ (-c_n).
Siano  H = ∑ b_n = lim_n(b₁+ ... +b_n)  e  K = ∑ c_n = lim_n(c₁+ ... +c_n). Segue che ∑ a_n = lim_n(a₁+ ... +a_n) = lim_n(b₁+ ... +b_n + c₁+ ... +c_n) = H + K.

Una serie convergente ma non assolutamente convergente viene detta condizionatamente (o semplicemenete o non assolutamente) convergente.

NOTA 2.
Il cambiamento arbitrario di un numero finito di termini di una serie non incide sulla sua convergenza / non convergenza (ma, solo, sul valore dell'eventuale somma). Infatti se il termine K-esimo è il termine di posto massimo che viene cambiato, per N>K la nuova somma fino al posto N (S'_N) è uguale alla vecchia (S_N) a meno del numero D pari alla differenza dovuta alla sosituzione operata: S'_N = S_N+D. E S'_N ha limite finito se e solo se lo ha S_N.

NOTA 3.
È facile vedere che se ∑a_n e ∑b_n convergono allora ∑(a_n+b_n) converge alla somma di esse.
Nel caso in cui ∑a_n e ∑b_n convergano assolutamente si ha che converge assolutamente (al prodotto delle loro somme) anche la "serie prodotto" (detta anche prodotto di Cauchy delle due serie di partenza) ∑c_n ottenuta pensando gli a_i e i b_i come coefficienti del termine di grado i-esimo di due polinomi e c_i come il coefficiente i-esimo del polinomio prodotto:
c₀ = a₀b₀
c₁ = a₀b₁+a₀b₁
c₂ = a₀b₂+a₁b₁+a₂b₀
...
[se a_i = α_ixⁱ e b_i = β_ixⁱ ho c_n = (α₀β_n+...+α_nβ₀)xⁿ]
La cosa risulterà utile quando si considererà il prodotto tra due serie di potenze.

NOTA 4. Per la convergenza di ∑(-1)n a(n) non basta che a(n) → 0; si è sicuri della convergenza se, inoltre, la successione a(n), almeno da un certo n in poi, decresce; controesempio:   1 - 1/4 + 1/3 - 1/16 + 1/5 - 1/36 + ...,  ossia a(n) = 1/n per n dispari, 1/n2 per n pari. Infatti gli addendi negativi tendono a 0 molto più lentamente di quelli positivi per cui le variazioni non tendono a compensarsi: la somma tende a comportarsi come se, da un certo punto in poi, ci fossero solo gli addendi di posto dispari. Del resto la somma 1/4+1/16+1/16+... converge mentre 1+1/3+1/5+... diverge; se la serie data convergesse, allora (per la Nota 3) dovrebbe convergere anche la somma di essa e di 1/4+1/16+1/16+..., che è, appunto, la serie formata dai soli termini di posto dispari, 1+1/3+1/5+..., che sappiamo invece divergere: assurdo.     Nel grafico a destra si vede bene come il contributo dei termini di posto pari tenda a diventare trascurabile.

NOTA 5.
Trucco.  ∑_n=1..∞ ( 1/√n − 1/√(n+1) ) ha la somma parziale di ordine n uguale a
1/√1−1/√2 + 1/√2−1/√3 + ... + 1/√n−1/√(n+1) = 1 − 1/√(n+1) che tende a 1 per n → ∞. Quindi la serie converge a 1.
Idea: vedere se una serie si riesce a riscrivere nella forma "telescopica" ∑_n=1..∞( a(n)-a(n+1) ) e, quindi, a ricondurne lo studio della convergenza a quello di a(1)-a(n) .
• Es.:  1/( n(n+1) ) può essere scomposto in due addendi frazionari con a denominatore n e n+1:
1/( n(n+1) ) = 1/n − 1/(n+1).  Quindi ∑_n=1..∞1/( n(n+1) ) si comporta come la successione 1 − 1/n, che convege a 1.
Nota. Quest'ultima serie è nota anche come serie di Mengoli, uomo di cultura (matematico, filosofo, uomo di legge, …) vissuto a cavallo del 1650, allievo di Bonaventura Cavalieri (a cui si deve, assieme a Leibniz e Newton, la nascita del calcolo infinitesimale). Osserviamo che ∑_n=1..∞1/( n(n+1) ) non equivale a ∑_n=1..∞1/n − ∑_n=1..∞1/(n+1) in quanto queste due serie divergono. Vedi anche la nota seguente.
• Altro es.:  ∑_n=1..∞ log(1+1/n)  ha il termine n-esimo che tende a 0 ma log(1+1/n) = log((n+1)/n) = log(n+1)−log(n) per cui la serie è telescopica e si comporta come log(n+1)−log(1) = log(n+1), che diverge (alla divergenza di questa serie potevi, comunque, arrivare in altri modi).

NOTA 6.
La serie convergente non assolutamente ∑_n=1..∞ (-1)ⁿ1/n  può essere riordinata in modo da divergere a ∞ o a -∞ o in modo da convegere a un qualunque numero reale L. Es.: prendiamo gli addendi positivi (1+1/3+...) fino a che superiamo 2.1 (1+1/3+...+1/19 = 2.13...), poi aggiungiamo -1/2 (1+1/3+...+1/19-1/2), così da scendere sotto a 2.1; poi aggiungiamo i successivi termini positivi fino a che superiamo nuovamente 2.1, poi aggiungiamo -1/4; e così via. In questo modo otteniamo una serie
1+1/3+...+1/19 -1/2 + 1/21+1/23+...+1/51 - 1/4 + 1/53+...
che converge a 2.1 (oscilla attorno a 2.1 con oscillazione di ampiezza che si riduce tendendo a 0).
La cosa può essere generalizzata a tutte le serie convergenti non assolutamente.
Invece una serie assolutamente convergente (e, in particolare, una serie convergente a termini positivi) comunque venga riordinata continua a convergere allo stesso valore.

NOTA 7.
Una generalizzazione del criterio di Leibniz, nota come criterio di Dirichlet, asserisce che  ∑_n=1..∞ a_nb_n  converge se a_n → 0 decrescendo e se esiste un M tale che |b₁+…+b_n| < M per ogni n  (non si chiede che b_n oscilli tra 1 e −1, ma che la somma dei b_n sia limitata).  Esempio d'uso:  ∑_n=1..∞ a_nsin(n)  converge per ogni a_n che tende a 0 decrescendo.

The infinite series

For a particular series, one or more of the common convergence tests may be most convenient to apply.