The First Derivative: Maxima and Minima

Consider the function

f(x) = 3x4-4x3-12x2+3
on the interval [-2,3]. We cannot find regions on which f is increasing or decreasing, relative maxima or minima, or the absolute maximum or minimum value of f on [-2,3] by inspection. Graphing by hand is tedious and imprecise. Even the use of a graphing program will only give us an approximation for the locations and values of maxima and minima. We can use the first derivative of f, however, to find all these things quickly and easily.

Increasing or Decreasing?

Let f be continuous on an interval I and differentiable on the interior of I. Then, by the Mean Value Theorem:

  • If f ′(x) > 0 for all x ∈ (interior of I), then f is increasing on I.

  • If f ′(x) < 0 for all x ∈ (interior of I), then f is decreasing on I.

Example

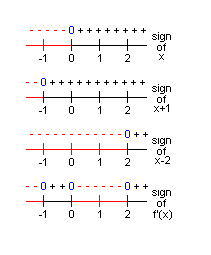
The function f(x) = 3x4-4x3-12x2+3 has first derivative

f ′(x)
=
12x3 - 12x2 -24x
=
12x(x2 -x - 2)
=
12x(x+1)(x-2).

Thus, f(x) is increasing on [-1,0] U [2, ∞) and decreasing on (-∞,-1] U [0,2].

Relative Maxima and Minima

Relative extrema of f occur at critical points of f, values x0 for which either f ′(x0) = 0 or f ′(x0) is undefined.

First Derivative Test

Suppose f is continuous at a critical point x0.

  • If f ′(x) > 0 on an open interval extending left from x0 and f ′(x) < 0 on an open interval extending right from x0, then f has a relative maximum at x0.

  • If f ′(x) < 0 on an open interval extending left from x0 and f ′(x) > 0 on an open interval extending right from x0, then f has a relative minimum at x0.

  • If f ′(x) has the same sign on both an open interval extending left from x0 and an open interval extending right from x0, then f does not have a relative extremum at x0.

In summary, relative extrema occur where f ′(x) changes sign.

Example

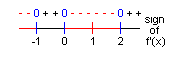Our function f(x) = 3x4-4x3-12x2+3 is differentiable everywhere on [-2,3], with f ′(x) = 0 for x = -1,0,2. These are the three critical points of f on [-2,3]. By the First Derivative Test, f has a relative maximum at x = 0 and relative minima at x = -1 and x = 2.

Absolute Maxima and Minima

  • If f has an extreme value on an open interval, then the extreme value occurs at a critical point of f.

  • If f has an extreme value on a closed interval, then the extreme value occurs either at a critical point or at an endpoint.

According to the Extreme Value Theorem, if a function is continuous on a closed interval, then it achieves both an absolute maximum and an absolute minimum on the interval.

Example

Since f(x) = 3x4-4x3-12x2+3 is continuous on [-2,3], f must have an absolute maximum and an absolute minimum on [-2,3]. We simply need to check the value of f at the critical points x = -1,0,2 and at the endpoints x = -2 and x = 3:

f(-2)
=
35,
f(-1)
=
-2,
f(0)
=
3,
f(2)
=
-29,
f(3)
=
30.

Thus, on [-2,3], f(x) achieves a maximum value of 35 at x = -2 and a minimum value of -29 at x = 2.

We have discovered a lot about the shape of f(x) = 3x4-4x3-12x2+3 without ever graphing it! Now take a look at the graph and verify each of our conclusions.

Graph it!

Key Concepts [index]

  • Increasing or Decreasing?

    Let f be continuous on an interval I and differentiable on the interior of I. If f ′(x) > 0 for all x ∈ I, then f is increasing on I. If f ′(x) < 0 for all x ∈ I, then f is decreasing on I.

  • Relative Maxima and Minima

    By the First Derivative Test, relative extrema occur where f ′(x) changes sign.

  • Absolute Maxima and Minima

    If f has an extreme value on a closed interval, then the extreme value occurs either at a a critical point or at an endpoint.