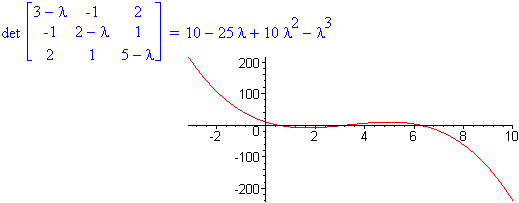
Forme quadratiche

Una forma quadratica (reale) di x1, x2, ..., xN  è un polinomio di 2° grado in x1, x2, ..., xN (a coefficienti reali) con tutti i termini di grado 2.

Un polinomio di questo tipo può essere scritto come (il determinante della matrice 1×1)  X t ×A×X  con A matrice simmetrica, dove X è il vettore colonna x1, x2, ..., xN  (ovvero: X×A×X t dove X è inteso come vettore riga).
Esempio 1:

2x2 + 4 xy + 5y2     X =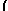 

x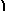

      A =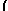 

2     2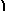



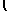y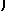



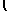2 5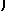

X×A×X t = [ x(2x+2y) + y(2x+5y) ] = [2x2 + 4 xy + 5y2]

Esempio 2:

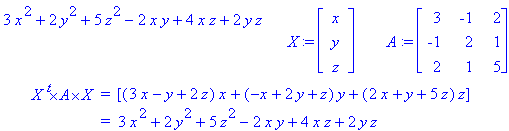
Provate a capire come è fatta, in generale, questa matrice (ossia, A[i,j] che cos'è?).

Esercizio:  Trovate la forma quadratica associata alla matrice 3×3 fatta tutta di 1 e calcolatene gli autovalori.

Ricordiamo (vedi) che ogni matrice reale simmetrica ha autovalori REALI, ai quali corrispondono autovettori ortogonali.

Nell'esempio 1, risolvendo (2-λ)(5-λ)-4 = 0 trovo gli autovalori λ1 = 1 e λ2 = 6.
Per trovare gli autovettori (x,y) risolvo  2x+2y = λx AND 2x+5y = λy.
Per λ1 ottengo x = -2y, ossia gli autovettori h(-2,1); per λ2 ottengo y = 2x, ossia gli autovettori h(1,2).

Nella figura a destra: il grafico di 2x2 + 4 xy + 5y2 = 10, i due autovettori (ortogonali) (1,2) e (-2,1), e i due autovettori ortonormali k(1,2) e k(-2,1) con k = 1/√5.
Se assumo questi come base per un nuovo sistema di riferimento, allora (vedi):
A assume la forma B = Λ dove Λ è la matrice diagonale che ha sulla diagonale i due autovalori 6 (corrispondente al nuovo primo versore) e 1 (corrispondente al secondo), che può essere espressa anche come B = P-1×A×P dove P è la matrice di transizione (le sue colonne sono i due autovettori), che risulta essere ortogonale (P t = P-1: vedi), essendo i due autovalori ortogonali e di modulo 1.
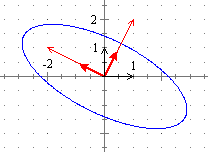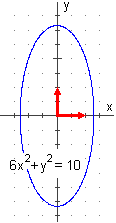Se indico con X' le nuove coordinate ( X' t = [x',y'] ),  ho X = P×X', per cui la forma quadratica  X t ×A×X  nel nuovo sistema diventa:		 

   (P×X') t ×A×P×X' = X' t ×(P t ×A×P)×X' = X' t ×(P-1×A×P)×X' = X' t ×Λ×X' = λ2x'2 + λ1y'2 = 6x'2 + y'2
A sinistra la stessa curva considerata sopra, rappresentata nel nuovo sistema di riferimento (nella figura, per comodità, le nuove coordinate sono state indicate ancora con x e y).

Questa possibilità di trasformare le forme quadratiche nella forma diagonale Σiλixi2 appena vista, oltre a facilitare lo studio di curve e superfici del secondo ordine, come nell'esempio considerato, ha varie altre applicazioni. Particolarmente utile è la seguente proprietà, che deriva immediatamente dalla rappresentazione in forma diagonale:
una forma quadratica F(X) =  X t ×A×X 
è definita positiva (ossia è positiva per ogni X ≠ 0) sse ha tutti gli autovalori positivi, è definita negativa (ossia è negativa per ogni X ≠ 0) sse ha tutti gli autovalori negativi;
è semidefinita positiva (ossia F(X) ≥ 0 per ogni X ≠ 0) sse ha tutti gli autovalori ≥ 0, è semidefinita negativa (ossia F(X) ≤ 0 per ogni X ≠ 0) sse ha tutti gli autovalori F(X) ≥ 0.

Nel caso dell'es. 1 gli autovalori, 1 e 6, sono positivi, per cui la forma quadratica è definita positiva.
La forma dell'es. 2, che possiamo scrivere x2+(x-y)2+(x+2z)2+(y+z)2, è sicuramente definta positiva. La corrispondente matrice ha dunque autovalori positivi. Verifichiamolo graficamente.