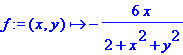
Gradiente

Consideriamo la funzione R^2 -> R:

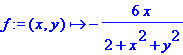
Grafico e curve di livello in [-6,6]×[-5,5]×[-2,2]:


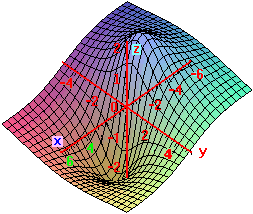
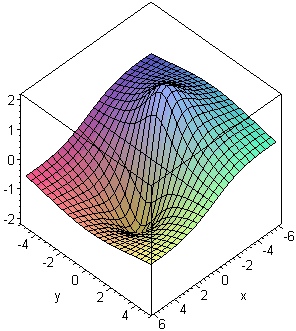
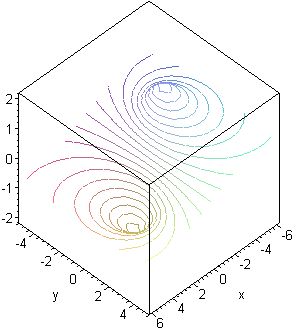
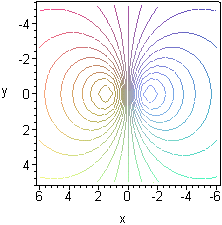
Ottengo tutto con WolframAlpha introducendo:  plot z=-6*x/(2+x^2+y^2), -6<=x<=6, -5<=y<=5

Gradiente di f: è la funzione vettoriale che ha come componenti le due derivate parziali di f, indicata con ∇f o con grad(f):
∇f(x,y) = (∂f(x,y)/∂x, ∂f(x,y)/∂y).
Nel nostro caso:

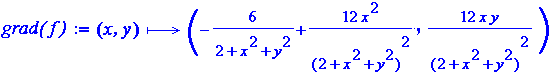
 In (√2,0) il gradiente, ossia le due derivate parziali si annullano. Lo stesso accade in (-√2,0). Questi sono i due punti di estremo (minimo e massimo). La cosa e' in accordo con le stime grafiche fattibili osservando le curve di livello.

Ottengo tutto con WolframAlpha introducendo:  grad ( -6*x/(2+x^2+y^2) )

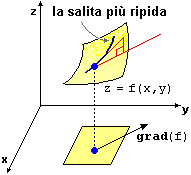
Nota. Nel nostro caso, invece di ∇f(x,y), avremmo anche potuto scrivere ∇x,y(6x/(2+x2+y2)) o gradx,y(6x/(2+x2+y2)), specificando ordinatamente le variabili rispetto a cui si deriva. Ad es. ∇y,z(6x/(2+x2+y2))  è  (12xy/(2+x2+y2)2, 0).

Il gradiente del campo scalare f (CAMPO scalare/vettoriale: grandezza scalare/vettoriale che dipende dalla posizione; nel nostro caso f(x,y) che dipende da (x,y)) e' il vettore (orizzontale) che indica la direzione in cui cresce piu' rapidamente f. Il suo modulo rappresenta la velocita' di questo aumento, ovvero la pendenza (positiva) della superficie lungo tale direzione.
[nel caso "univariato" il gradiente corrisponde alla derivata, il suo modulo è il valore assoluto della pendenza del grafico, il segno della pendenza è il segno della derivata]
Il gradiente (se diverso da 0) è perpendicolare alla curva di livello passante per (x,y).
Le componenti del gradiente indicano la rapidita' della variazione nelle direzioni degli assi x e y. Le altre derivate direzionali (ossia le proiezioni del gradiente nelle altre direzioni) si trovano facendo i prodotti scalari del gradiente per i versori delle varie direzioni. La direzione di una curva di livello passante per un punto P indica la direzione lungo cui il gradiente si annulla.		   
Come nel caso di una funzione in una variabile il fatto che la sua derivata in x sia nulla non e' sufficiente per dedurre che in x vi sia un max o un min relativo (potrebbe esservi un flesso), cosi' nel caso di una funzione di due variabili non basta che il gradiente in P sia nullo (ossia che P sia un punto stazionario) affinche' in P vi sia un estremo relativo. Nel caso dell'esempio precedente per (√2,0) e (-√2,0) la cosa ci era assicurata dall'andamento del grafico.

Un'altra funzione: f:=(x,y) -> sin(x)*sin(y).
[a destra le curve di livello alle quote 0.9, 0.7, 0.5 (in blu), -0.9, -0.7, -0.5 (in rosso), 0 (in verde)]

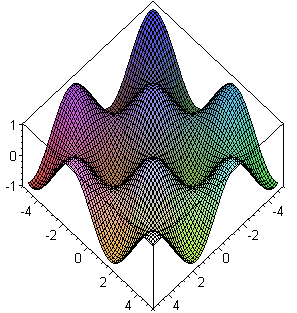
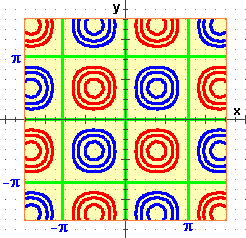
Ottengo tutto con WolframAlpha introducendo:  plot z=sin(x)*sin(y), -5<=x<=5, -5<=y<=5

Dove si azzera il gradiente, cos(x) sin(y) i + sin(x) cos(y) j:

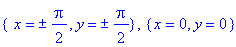
 In questo caso dal grafico capiamo che (0,0) [e gli altri punti che si ottengono "aggiungendo periodi"] non e' di max ne' di min (e' un punto di sella: è di minimo lungo la "cresta dei monti" e di massimo lungo la "starda del valico"), che (π/2,π/2) e il suo simmetrico rispetto (0,0) sono di max e che (-π/2,π/2) e il suo simmetrico rispetto a (0,0) sono di min. Nei punti di sella le curve di livello si intersecano; avvicinandosi a quelli di min/max tendono a ridursi ad un punto. Come si potrebbe procedere senza grafico?

Polinomio di Taylor

È utile approfondire qualche analogia col caso univariato (funzioni di una variabile).
• Con d f(x) indichiamo il differenziale di f(x), cioè l'approssimazione di Δf(x) che si ottiene supponendo che la funzione f avvicinadosi a x sia lineare:  Δf(x) per Δx→0 (ossia quando diventa infinitesimale) tende a confondersi con d f(x).
Fissato x0, y = f(x0) + f'(x0)(x-x0) è l'equazione della retta tangente al grafico in x0.
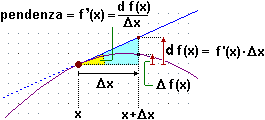• Nel caso bivariato, posto P0 = (x0, y0), z = f(P0) + ∇f(P0) · (P−P0), ossia z = f(x0,y0) + f 'x(x0,y0)(x-x0) + f 'y(x0,y0)(y-y0), è l'equazione del piano tangente a z = f(x,y) in P0. 		  
Il termine ∇f(P) · (ΔP), che rappresenta l'approssimazione della variazione della funzione f al variare di P di ΔP che si ottiene considerando, invece di f, la funzione che ha per grafico il piano tangente in P, viene chiamato il differenziale (totale) di f(x,y) e indicato d f(x,y).

• Nel caso univariato, si può approssimare f invece che con una funzione lineare con una funzione polinomiale di grado superiore. Queste approssimazioni si basano sul concetto di polinomio di Taylor:
Δf = d f + d2f / 2 + d3f / 3! + …  dove d n f(x) = f (n)(x) dxn è il differenziale di ordine n di f(x).
Ricordiamo che:
−  dxn sta per (dx)n
−  dx risulta essere uguale a Δx
−  d2f(x) non è altro che d(d(f(x)), il differenziale del differenziale: considerando fissato l'incremento Δx, d(d(f(x)) = d(f '(x) Δx) = d( f '(x) )Δx = (f "(x) Δx) Δx = f "(x) (Δx)2
−  d3f(x) può essere pensato come d(d(d(f(x))), …

Nel caso di f(x) = sin(x), df(x) = cos(x)Δx e d2f(x)Δx = −sin(x)(Δx)2, per cui attorno a π/2, tenendo conto che Δx = x − π/2, sin(x) (fermandosi al polinomio di ordine 2) è approssimabile con sin(π/2) + cos(π/2)(x−π/2) − sin(π/2)/2(x−π/2)2 = 1 + 0 − (x−π/2)2/2 = 1 − (x−π/2)2/2.
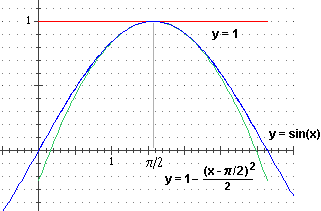A lato sono rappresentate graficamente, oltre a f, sia l'approssimazione attorno a π/2 si ordine 1 (che coincide con quella di ordine 0 essendo f '(π/2) = 0) che quella di ordine 2. Dalla prima si capisce che in π/2 la tangente è orizzontale (punto stazionario), dalla seconda che la concavità è verso il basso (punto di massimo, non di minimo o di flesso). 		  
Se f ''(π/2) fosse stata nulla, per stabilire che tipo di punto stazionario è, avremmo potuto calcolare f '''(π/2) e considerare il polinomio di ordine 3.
Invece che ricorre all'esame di y = f(π/2)+f '(π/2)(x-π/2) e di y = f(π/2)+f '(π/2)+f "(π/2)(x-π/2)2 avremmo potuto più semplicemente studiare il segno di f ' (vedi) e di f " (vedi), in π/2:
se f '(π/2)=0 e f "(π/2)>0, in π/2 si ha tangenza orizzontale con concavità verso il basso,
se f '(π/2)=0 e f "(π/2)<0 in π/2 si ha tangenza orizzontale con concavità verso l'alto,
se f '(π/2)=0, f "(π/2)=0 e f '''(π/2)≠0, in π/2 si ha tangenza orizzontale senza estremo,
se f '(π/2)=0, f "(π/2)=0, f '''(π/2)=0 e f (4)(π/2)≠0 l'estremo esiste, e così via.

• Nel caso bivariato, si può procedere in modo simile, tenendo conto che nel polinomio di Taylor
Δf = d f + d2f / 2 + d3f / 3! + …
−  d f(x,y) = ∇f(P) · (ΔP) = f 'x (x,y) Δx + f 'y (x,y) Δy
−  d 2 f(x,y) = d (d f(x,y) ) = ∇(f 'x (x,y) Δx + f 'y (x,y) Δy) · (ΔP) =
f "xx (x,y) Δx Δx + f "xy (x,y) Δy Δx + f "yx (x,y) Δx Δy + f "yy (x,y) Δy Δy =
f "xx (x,y) (Δx)2 + 2 f "xy (x,y) Δx Δy + f "yy (x,y) (Δy)2
−  d 3 f(x,y) = …

Vediamo ad es. il comportamento di f(x,y) = sin(x) sin(y), già considerata sopra, attorno a (π/2, π/2).
d f(x,y) = cos(x)sin(y)Δx +sin(x)cos(y)Δy
f(x,y) = f(π/2,π/2) + cos(π/2)sin(π/2)Δx +sin(π/2)cos(π/2)Δy + ... = 1 + ...
d 2 f(x,y) = − sin(x)sin(y)(Δx)2 + 2 cos(x)cos(y)Δx Δy − sin(x)sin(y)(Δy)2
f(x,y) = 1 + (− sin(π/2)sin(π/2)(Δx)2 + 2 cos(π/2)cos(π/2)Δx Δy − sin(π/2)sin(π/2)(Δy)2)/2 + ... = 1 − (x−π/2)2/2 − (y−π/2)2/2 + ...

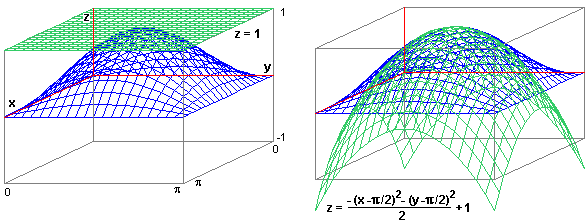
Sotto sono rappresentate, attorno a (π/2, π/2), sia f che le funzioni polinomiali corrispondenti ai polinomi di Taylor di ordini 1 e 2. Dal fatto che la seconda ha grafico con la concavità verso il basso si può dedurre (omettiamo i dettagli della dimostrazione) che in (π/2, π/2) si ha un massimo relativo (anche se in questo caso particolare abbiamo già visto che era facile arrivare a questa conclusione con ragionamenti e procedimenti più semplici).

Attorno a (0,0), invece:
f(x,y) = f(0,0) + cos(0)sin(0)Δx + sin(0)cos(0)Δy + ... = 0 + 0(x − 0) + 0(y − 0) + ... = 0 + ...
f(x,y) = 0 + (− sin(0)sin(0)(Δx)2 + 2 cos(0)cos(0)Δx Δy − sin(0)sin(0)(Δy)2)/2 + ... = x y + ...

z = 0 è tangente a z = f(x,y) in (0,0) ma la funzione polinomiale di 2° grado che approssima f ha grafico (z = xy) che attorno al punto ha punti sia sopra che sotto al piano tangente, per cui (0,0) non è un punto di estremo:

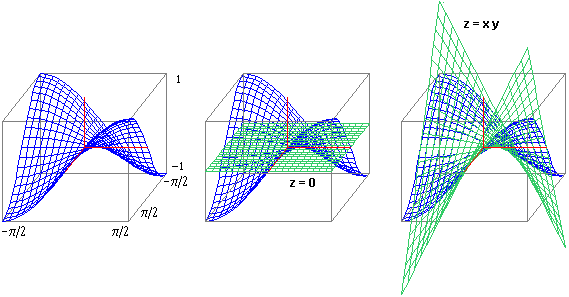
Cerchiamo un modo rapido, analogo allo studio del segno della derivata seconda nel caso univariato, per stabilire, di fronte a un punto P0 in cui il gradiente sia nullo, se esso sia un punto di estremo.
f(P0) + f "xx (P0) (x-x0)2 + 2 f "xy (P0) (x-x0) (y-y0) + f "yy (P0) (y-y0)2 è l'approssimazione polinomiale di f(x,y) attorno a P0. Supponiamo che le derivate seconde non siano tutte nulle.
Il suo grafico è una superficie simmetrica rispetto alla retta verticale passante per P0 (se cambio segno a x-x0 e y-y0 ottengo un termine equivalente), per cui le sue curve di livello (che corrispondono a eq. polinomiali di grado 2), a quote diverse da f(P0), sono ellissi o iperboli o coppie di rette parallele. Nel primo caso avremo un punto di estremo, nel secondo un punto di sella, nel terzo potremmo avere un punto di entrambi i tipi (vedi l'esempio in appendice).
Per stabilire il tipo di conica semplifichiamo la scrittura prendendo un sistema di riferimento X,Y,Z centrato in P0 in modo da descrivere la superficie con Z = f "xx (P0) X2 + 2 f "xy (P0) XY + f "yy (P0) Y2 e la curva di livello alla quota Q con   f "xx (P0) X2 + 2 f "xy (P0) XY + f "yy (P0) Y2 − Q = 0
Se vi è un asintoto con pendenza p, per X → ∞ o per X → -∞ lungo la curva Y/X tende a p; divido quindi per X2 e suppongo che Y/X tenda a p; l'equazione diventa   f "xx (P0) + 2 f "xy (P0) p + f "yy (P0) p2 = 0.
− Se il discriminante  f "xy (P0)2 − f "yy (P0) f "xx (P0)  è positivo trovaimo due valori di p, ossia due asintoti: le curve di livello sono iperboli, e il punto è di sella;
− se il discriminante è nullo le curve di livello sono coppie di rette: non possiamo decidere;
− se il discriminante è negativo le curve di livello sono ellissi, e il punto è di estremo relativo;
− in tal caso, per decidere se le curve di livello stanno sopra o sotto al piano tangente basta vedere quanto vale Z in un punto qualunque diverso da (0,0); prendo (1,0), in cui Z = f "xx (P0); dunque si ha un minimo se f "xx (P0) > 0, un massimo se f "xx (P0) < 0.

Rivediamo f(x,y) = sin(x) sin(y).
f "xy (P0)2 − f "yy (P0) f "xx (P0) = (cos(x0)cos(y0))2−(sin(x0)sin(y0))2 per P0 = (π/2,π/2) vale -1: punto di estremo; f "xx (P0) = −sin(x0)sin(y0) vale -1: punto di massimo;  per P0 = (0,0) il discriminante vale 1: punto di sella.

Matrice Hessiana

Il discriminante f "xy (x,y)2 − f "yy (x,y) f "xx (x,y) può essere espresso in forma compatta come l'opposto del determinante della matrice Hessiana così definita:  H f (P) = (Di j(f)(P))i j, ossia:

H f (x,y) = 





f "xx (x,y)     f "xy (x,y)











f "yx (x,y) f "yy (x,y)





 = 

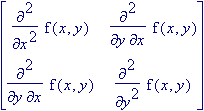Si noti che la matrice è simmetrica (ossia è uguale alla sua trasposta) in quanto f "xy = f "yx.
Dunque, in un punto P in cui il gradiente è nullo (e in un intorno del quale il campo abbia derivate seconde continue) se il determinante di H f (P) è negativo si ha un punto di sella, se il determinante è positivo si ha un minimo/massimo (locale) a seconda che D11 sia positivo/negativo (si noti l'analogia con il test della derivata seconda per il caso a 1 input). Se il det. è nullo non si puņ concludere nulla in questo modo. Il determinante della matrice hessiana viene chiamato hessiano.

Nel caso di f(x,y) = sin(x) sin(y) la matrice Hessiana è

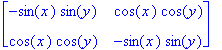
e il suo determinante è:

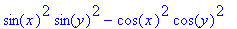
Con WolframAlpha introduco:  Hessian of sin(x)*sin(y)

Per ricordarsi la casistica, si può pensare alle due funzioni f(x,y) = x2+y2 e f(x,y) = x·y, entrambe con gradiente nullo in (0,0):
• nel primo caso (vedi figura a destra) siamo di fronte a una funzione che si annulla e ha minimo solo in (0,0); le curve di livello sono cerchi centrati in (0,0); le derivate miste, ∂2f(x,y)/(∂x ∂y) = ∂2f(x,y)/(∂y ∂x), sono nulle e le altre due derivate seconde, ∂2f(x,y)/(∂x2) e ∂2f(x,y)/(∂y2), valgono 2, per cui il determinante della matrice Hessiana è 4: positivo (punto di max o min); D11(f) vale 2: positivo (punto di min).  
  • nel secondo caso (vedi figura a sinistra) siamo di fronte a una funzione che in (0,0) ha un punto di sella (ivi la curva di livello è formata dagli assi x e y; le altre curve di livello sono iperboli; le derivate miste valgono 1 e le altre due derivate seconde sono nulle, per cui il determinante della matrice Hessiana è −1: negativo (punto di sella).

Campi scalari di 3 o più variabili

Abbiamo visto che d f(x,y) e più in generale d f(P), con P = (x1,…,xn), è esprimibile come ∇f(P) · ΔP.
La matrice Hessiana consente di scrivere in forma compatta anche d 2 f(x,y), ossia f "xx (x,y) (Δx)2 + 2 f "xy (x,y) Δx Δy + f "yy (x,y) (Δy)2. È facile verificare che tale espressione equivale a  ΔP × H f (P) × (ΔP)t dove l'ultimo fattore è la trasposta di ΔP, ossia è il vettore colonna (Δx,Δy).
Questa osservazione ci consente di utilizzare, per lo studio dei punti di estremo, le proprietà delle forme quadratiche (vedi).

La cosa vale, più in generale, per d 2 f(P) con P = (x1,…,xn).
Anche per n > 2 la matrice Hessiana è simmetrica (le derivate miste Di j e Dj i, se continue, come stiamo ipotizzando, coincidono).

Se (in un intorno di P in cui il gradiente si annulla) la matrice Hessiana ha autovalori positivi la forma quadratica corrispondente, ossia d 2 f(P), è definita positiva, per cui sta sopra al piano tangente: si ha un punto di minimo.
Analogamente, se la matrice Hessiana ha autovalori negativi si ha un punto di massimo.
Se ha autovalori sia positivi che negativi, si ha un punto di sella.
Se gli autovalori sono tutti nulli, non si può concludere nulla. Occorrerebbe procedere considerando d 3 f(P).

Nel caso di f(x,y) = sin(x) sin(y) la matrice Hessiana per (x,y) = (π/2,π/2) ha autovalori -1 e -1 (-1 con molteplictà 2) per cui d 2 f(P) è definita negativa e si ha un punto di massimo. Per (x,y) = (π/2,-π/2) ha autovalori 1 e 1 (1 con molteplictà 2) per cui d 2 f(P) è definita positiva e si ha un punto di minimo. Per (x,y) = (0,0) ha autovalori 1 e -1 per cui d 2 f(P) è indefinita e si ha un punto di sella.

Esercizio. Determinare e classificare i punti critici di (x,y,z) x2y+y2z+z2-2x  e di  (x,y,z) xy+x2z-x2-y-z2

[index]

Appendice

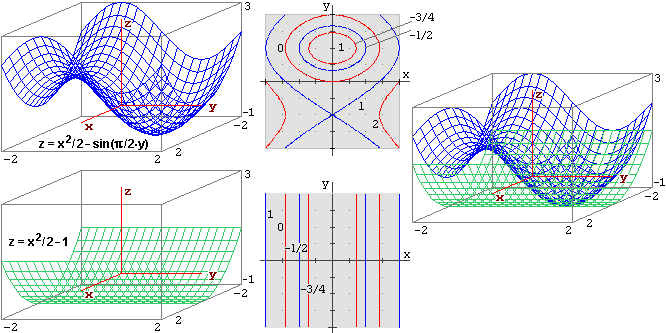
Sotto sono rappresentate graficamente una funzione di (x,y) e il suo polionomio di Taylor di ordine 2 in (0,1) dove il gradiente si annulla. Le curve di livello del polinomio di Taylor sono coppie di rette parallele. In questo caso il punto è di minimo relativo. Invece in (0,-1), in cui il gradiente si annulla e il polinomio di Taylor (z = x2/2+1) ha nuovamente rette parallele per curve di livello, si ha un punto di sella.

Vedi qui per il calcoli con R.