In any inner-product space, we can choose the basis in which to work. It often greatly simplifies calculations to work in an orthogonal basis. For one thing, if S = {v₁, v₂,…:, v_n} is an orthogonal basis for an inner product space V, then it is a simple matter to express any vector w ∈ V as a linear combination of the vectors in S:

w = <w,v1> || v1 ||2 v1 + <w,v2> || v2 ||2 v2 +…:+ <w,vn> || vn ||2 vn.

That is, w has coordinates < w,v1 > ||v1||2 v1   < w,v2 > ||v2||2 v2  . . . < w,vn > ||vn||2 vn   T relative to the basis S.

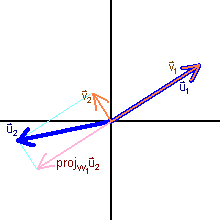
Given an arbitrary basis {u₁, u₂, …:, u_n} for an n-dimensional inner product space V, the Gram-Schmidt algorithm constructs an orthogonal basis {v₁, v₂,…:, v_n} for V:       

Step 1:		Let v1 = u1
Step 2:		Let v2 = u2 - projW1u2 = u2 - [ <u2,v1> / || v1||2 ]v1 where W1 is the space spanned by v1, and projW1u2 is the orthogonal projection of u2 on W1.
Step 3:		Let v3 = u3 -projW2 u3 = u3- [ <u3,v1> / || v1 ||2 ]v1 - [ <u3,v2> / || v2 ||2 ]v2 where W2 is the space spanned by v1 and v2.
Step 4:		Let v4 = u4 -projW3 u4 = u4- [ <u4,v1> / || v1 ||2 ]v1 - [ <u4,v2> / || v2 ||2 ]v2 - [ <u4,v3> / || v3 ||2 ]v3 where W3 is the space spanned by v1, v2 and v3.
	. . .

Continue this process up to v_n. The resulting orthogonal set {v₁,v₂,…:,v_n} consists of n linearly independent vectors in V and so forms an orthogonal basis for V.

• To obtain an orthonormal basis for an inner product space V, use the Gram-Schmidt algorithm to construct an orthogonal basis. Then simply normalize each vector in the basis.

• For Rⁿ with the Eudlidean inner product (dot product), we of course already know of the orthonormal basis { (1,0,0,…:,0), (0,1,0,…:,0), …:, (0, …:,0,1)}. For more abstract spaces, however, the existence of an orthonormal basis is not obvious. The Gram-Schmidt algorithm is powerful in that it not only guarantees the existence of an orthonormal basis for any inner product space, but actually gives the construction of such a basis.

Example

Let V = R³ with the Euclidean inner product. We will apply the Gram-Schmidt algorithm to orthogonalize the basis { (1,-1,1),(1,0,1),(1,1,2)}.

Step 1:     v1

=

(1,-1,1)

Step 2:     v2	=	(1,0,1) - (1,0,1) · (1,-1,1) ||(1,-1,1)||2 (1,-1,1)
	=	(1,0,1) - 2 3 (1,-1,1)
	=	1 3 , 2 3 , 1 3 .

Step 3:     v3	=	(1,1,2) - (1,1,2) · (1,-1,1) ||(1,-1,1)||2 (1,-1,1) - (1,1,2) · (1/3,2/3,1/3) ||(1/3,2/3,1/3)||2 (1/3,2/3,1/3)
	=	(1,1,2) - 2 3 (1,-1,1) - 5 2 (1/3,2/3,1/3)
	=	(-1/2,0,1/2)

You can verify that { (1,-1,1),(1/3,2/3,1/3),(-1/2,0,1/2)} forms an orthogonal basis for R³. Normalizing the vectors in the orthogonal basis, we obtain the orthonormal basis

√3 3 , -√3 3 , √3 3 , √6 6 , √6 3 , √6 6 , -√2 2 , 0, √2 2 .

Given an arbitrary basis { u₁,u₂,…:,u_n} for an n-dimensional inner product space V, the Gram-Schmidt algorithm constructs an orthogonal basis { v₁,v₂,…:,v_n} for V:

Step 1:     Let v1	=	u1.
Step 2:     Let v2	=	u2 - <u2, v1> ||v1||2 v1.
Step 3:     Let v3	=	u3 - <u3, v1> ||v1||2 v1 - <u3, v2> ||v2||2 v2.