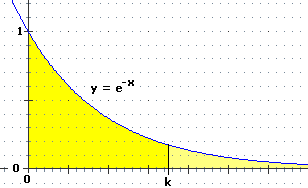Gli integrali impropri sono una generalizzazione degli integrali (secondo Riemann), che sono stati definiti solo per una funzione limitata e un intervallo finito.

Idea:  per calcolare l'area della figura illimitata compresa tra y = e–x e y = 0 che sta nel semipiano x ≥ 0 posso calcolare l'area della figura compresa tra y = e–x, y = 0, x = 0, x = k (k>0) e farne il limite per k che tende all'infinito. Per simmetria rispetto all'asse y dei grafici di y=exp(x) e y=(exp(-x) ho: ∫[0,k]e–xdx = ∫[-k,0]exdx = [ex]x=0–[ex]x=–k = 1–1/ek Questa è l'area della figura limitata a destra da x=k. Al tendere di k a ∞ 1–1/ek tende a 1: la figura illimitata che si ottiene ha area limitata (uguale a 1).

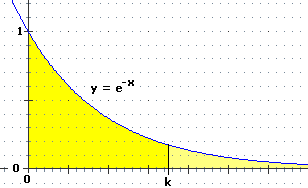∫_α^b f   o   ∫_(α,b] f   con f integrabile (secondo Riemann) in ogni intervallo chiuso [u,b] contenuto in (α,b]  (α numero reale in cui f non è definita o non è continua o α = -∞) indica l'eventale valore finito del limite:
lim _{u → α+} ∫_u^b f    se α reale,   ovvero   lim _{u → -∞} ∫_u^b f    se α = -∞

∫_a^β f   o   ∫_[a,β) f   con f integrabile (secondo Riemann) in ogni intervallo chiuso [a,v] contenuto in [a,β)  (β numero reale in cui f non è definita o non è continua o β = ∞) indica l'eventale valore finito del limite:
lim _{v → β-} ∫_a^v f    se β reale,   ovvero   lim _{v → ∞} ∫_a^v f    se β = ∞

Es.: esiste   ∫_[1,∞) 1/x² dx ?  Sì, e  ∫_[1,∞) 1/x² dx = 1.
lim _{x → ∞} ∫_[1,x] 1/t² dt  =  lim _{x → ∞} (-1/x+1) = 1
[è l'area tra  y = 1/x²  e  asse x  a destra della retta  y=1]

Es.: esiste   ∫_[1,∞) 1/x dx ?  No.
lim _{x → ∞} ∫_[1,x] 1/t dt  =  lim _{x → ∞} log(x) = ∞

Es.: esiste   ∫_(0,1] 1/√x dx ?  Sì, e  ∫_(0,1] 1/√x dx = 2.
lim _{x → 0+} ∫_[x,1] 1/√t dt  =  lim _{x → 0+} (2-2√x) = 2

I valori così definiti vengono chiamati integrali impropri [a volte, invece che dire che un integrale improprio non esiste, si dice che diverge e, invece che esiste, si dice che converge].
Ad essi si aggiungono gli integrali ottenibili estendendo agli integrali impropri la proprietà   ∫_a^c f + ∫_c^b f = ∫_a^b f

Es.: esiste   ∫[1,3] 1/(x-2)1/3 dx ?  L'integranda non è definita in 2, per cui il problema viene ricondotto all'esistenza degli integrali su [1,2) e (2,3], per vedere se si può porre ∫[1,3] 1/(x-2)1/3 dx = ∫[1,2) 1/(x-2)1/3 dx + ∫(2,3] 1/(x-2)1/3 dx. lim x → 2- ∫[1,x] 1/(t-2)1/3 dt  =  lim x → 2- 3/2(x-2)2/3 - 3/2(1-2)2/3 = -3/2 Quindi ∫[1,2) 1/(x-2)1/3 dx = -3/2. Analogamente si ha ∫(2,3] 1/(x-2)1/3 dx = 3/2. Dunque  ∫[1,3] 1/(x-2)1/3 dx = 0.

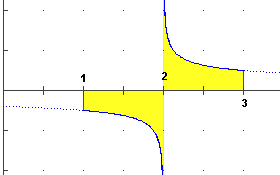Ragionando per simmetria, si poteva dedurre subito che l'integrale, se esiste, deve valere 0. Per stabilire se esiste si doveva però studiare che cosa accade su (2,3] o su [1,2).

Teorema del confronto per integrali impropri
È geometricamente intuitivo, ed è facile dimostrare, che:
Se |f(x)| ≤ g(x) su I e se g è integrabile su I, allora tale è f   (e se f non è integrabile non lo è g).

Es.:   ∫_[1,∞) 1/(1+x²) dx   esiste in quanto esiste  ∫_[1,∞) 1/x² dx  e se 1≤x≤∞  1/(1+x²) < 1/x²

Es.:   ∫_[1,∞) x/(1+x²) dx   non esiste in quanto non esiste  ∫_[1,∞) 1/x dx  e se 1≤x≤∞  x/(1+x²) ≥ x/(x²+x²) = 1/2·1/x.

Possiamo ottenere come corollario del precedente i seguenti altri criteri:
Se f(x) è un infinito di ordine inferiore o uguale rispetto a g(x) per x → α e | g | è integrabile su (α,b], allora tale è | f | , e a maggior ragione lo è f.
  e
Se f(x) è continua in [a,∞), se  ∫_[a,∞) f(x) dx  converge ed esite lim _x→∞ f(x), allora tale limite è nullo.

Es.:   ∫_(0,1] log(x)² dx   esiste in quanto esiste  ∫_(0,1] 1/√x dx  e per  x → 0+  log(x)²/(1/√x) → 0 (log(x) per x che tende a 0 è un infinito trascurabile rispetto a 1/x^p qualunque sia p positivo).

∫ x^-p dx     Se  0 < a (generalizzando quanto visto in vari esempi precedenti) si ha:
∫_a^∞ x^{– p} dx   converge a  a^1-p/(p-1)  se p > 1,  diverge (a ∞) altrimenti;
∫₀^a x^{– p} dx   converge a  a^1-p/(1-p)  se p < 1,  diverge (a ∞) altrimenti.

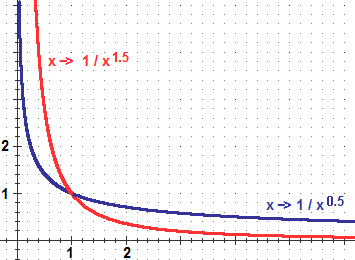
Es.: ∫_(2,3] 1/(x-2)^1/3 dx  converge in quanto 1/3<1 (penso (x-2)^1/3 come t^–1/3, integrato tra 0 e 1), e converge a 1^1-1/3/(1-1/3) = 3/2.

Esercizi. Studiare la convergenza di:
∫₀^∞ x / √(x⁴+1) dx     ∫_−∞^∞ e^-x2 dx     ∫₀^∞ 1 / √(x³+1) dx     ∫₀₊^∞ e^-√x / √x dx
∫₀₊¹⁻ log(x) / (1−x) dx     ∫₀₊¹⁻ dx / (√x log(x))     ∫₂^∞ dx / (x(log(x)^p)
[risp.: divergono il primo e il penultimo, e l'ultimo solo quando p non è maggiore di 1]