Integration by Parts
We will use the Product Rule for derivatives to derive a powerful
integration formula:
This formula frequently allows us to compute a difficult integral by
computing a much simpler integral.
Idea: cercare di fattorizzare l'integranda
come f·D(g) con D(f) (moltiplicato per g) più facile da sottoporre a integrazione,
se è facile
"vedere" D(g).
We often express the Integration
by Parts formula as follows:
Let
| u = f(x) |
|
dv =
g′(x) dx |
| du =
f′(x) dx |
|
v = g(x) |
Then the formula becomes
To integrate by parts, strategically choose u, dv and then apply
the formula.
Example 1
Let's evaluate ∫ xex dx.
Idea: cerco di togliermi dai piedi il fattore x sostituendolo con la sua derivata; exp(x) è
banale vederla come derivata.
• ∫(f·D(g)) = f·g - ∫(D(f)·g)
f(x)=x, g(x)=exp(x)
ex = Dx(ex)
xex = xDx(ex)
∫xexdx = xex - ∫Dx(x)exdx =
xex - ∫exdx = xex - ex (+C)
• or:
| u = x |
|
dv = ex dx |
| du = dx |
|
v = ex |
Example 2
∫ x2log(x) dx = #
Cerco di togliermi dai piedi log(x) che non è facilmente integrabile, a differenza della
sua derivata; x2 è facile vederlo come derivata:
# = ∫ Dx(x3/3)log(x) dx = x3/3 log(x) - ∫x3/3·1/x dx =
x3/3 log(x) - x3/9 (+c)
Example 2'
∫ log(x2+1) / x2 dx = #
Cerco di togliermi dai piedi log; x-2 è facile vederlo come derivata:
# = ∫ Dx(-x-1)log(x2+1) dx = -x-1 log(x2+1) + ∫x-1·1/(x2+1)·2x dx =
-log(x2+1)/x + 2∫1/(x2+1) dx = -log(x2+1)/x +
2 atan(x) (+c)
Example 3
∫ x2sin(3x) dx = #
Cerco di abbassare grado di x2 rimpiazzandolo con la derivata; sin(3x) è facile da vedere
come derivata:
# = ∫x2Dx(-cos(3x)/3)dx = -x2cos(3x)/3 -
∫2x(-cos(3x)/3)dx = #
abbasso di grado la x in:
∫x cos(3x)dx = x sin(3x)/3 - ∫sin(3x)/3
# = -x2 cos(3x)/3 + 2/9 x sin(3x) + 2/27 cos(3x) (+c)
Example 4
∫ sin(x)2 dx = #
Posso manipolare l'integranda pensando sin(x) come derivata:
# = ∫sin(x)sin(x) dx = ∫Dx(-cos(x))sin(x) dx = -cos(x)sin(x) -
∫(-cos(x))Dx(sin(x))dx =
-cos(x)sin(x) + ∫1-sin(x)2dx =
-cos(x)sin(x) + x - ∫sin(x)2dx
Quindi 2∫ sin(x)2 dx = x - cos(x)sin(x) e infine:
∫ sin(x)2 dx = (x - cos(x)sin(x))/2 (+c).
Integration by parts ``works'' on definite integrals as well:
⌠
⌡ |
b
a
|
u dv = uv |
∣
∣
∣ |
b
a
|
- |
⌠
⌡ |
b
a
|
v du. |
Example 5
We will evaluate
• Idea: cerco di rimpiazzare atan(x) con la derivata, che è qualcosa di polinomiale;
posso immaginare che nell'integranda ci sia un "·1", e penso 1 come derivata
di x  x: x:
atan(x) = Dx(x)·atan(x)
∫atan(x)dx = x·atan(x) - ∫x·1/(1+x2)dx = #
Idea : D(log(f(.)) = 1/f·D(f) = D(f)/f
# = x·atan(x) - log(1+x2)/2
∫[0,1]atan(x)dx = [x·atan(x)]x=0..1
- [log(1+x2)/2]x=0..1 = π/4 - log(2)/2.
• or: let
| u = arctan(x) |
|
dv = dx |
|
|
|
v = x |
|
|
= |
| x
arctan(x) |
∣
∣
∣ |
1
0
|
- |
⌠
⌡ |
1
0
|
x
1+x2
|
dx |
|
|
= |
| x arctan(x) |
∣
∣
∣ |
1
0
|
− |
1
2
|
ln (1+x2) |
∣
∣
∣ |
1
0
|
|
|
= |
|
|
= |
|
Sometimes it is necessary to integrate twice by parts in order to
compute an integral (in genere per trovare ∫f in termini
ancora di ∫f e poi risolvere l'equazione ottenuta rispetto a ∫f):
Example 6
Let's compute ∫ excos(x) dx.
• Idea: D(exp)=exp, exp(x)cos(x) = D(exp)(x)cos(x)
∫exp(x)cos(x) dx = ∫D(exp)(x)cos(x) dx = exp(x)cos(x) + ∫exp(x)sin(x) dx
Procedo in modo analogo sul nuovo integrale:
∫exp(x)sin(x) dx = ∫D(exp)(x)sin(x) dx = exp(x)sin(x) - ∫exp(x)cos(x) dx
Sono riuscito ad ottenere:
2∫exp(x)cos(x) dx = exp(x)cos(x) + exp(x)sin(x) (+C)
∫exp(x)cos(x) dx = (cos(x)+sin(x))exp(x)/2 (+C)
• or:
let
| u = ex |
|
dv = cos(x) dx |
| du = ex dx |
|
v = sin(x) |
Then ∫
excos(x) dx
= exsin(x) -
∫
exsin(x)
dx.
It is not clear yet that we've accomplished anything, but now let's
integrate the integral on the right-hand side by parts:
Now let
| u = ex |
|
dv = sin(x) dx |
| du = ex dx |
|
v = -cos(x) |
So ∫
exsin(x) dx
= - excos(x) +
∫
excos(x)
dx.
Substituting this into
∫
excos(x) dx = exsin(x)-∫
exsin(x) dx,
|
|
= |
| exsin(x)- |
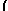

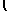 |
-excos(x)+ |
⌠
⌡ |
excos(x) dx |
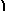

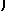 |
|
|
= |
| exsin(x)+ excos(x) - |
⌠
⌡ |
excos(x) dx. |
|
The integal ∫
excos(x) dx appears on both sides on the
equation, so we can solve for it:
| 2 |
⌠
⌡ |
excos(x) dx = exsin(x)+excos(x). |
Finally,
⌠
⌡ |
excos(x) dx = |
1
2
|
exsin(x)+ |
1
2
|
excos(x) +C, |
where the constant of integration is needed since the integral is indefinite.
Check
by Differentiating
A volte è utile il trucco di immaginare la presenza di un fattore "·1"
da interpretare come D(g):
Example 7
∫ log(x) dx = ∫ 1·log(x) dx = ∫ Dx(x)·log(x) dx =
x·log(x) − ∫ x·Dx(log(x)) dx = x·log(x) − ∫1 dx =
x·log(x) − x (+ c)
Attenzione al calcolo degli integrali definiti (spesso conviene ricondursi prima a un integrale indefinito):
Example 8
∫[1,e] x3 log(x)2 dx = (*)
∫ x3 log(x)2 dx = ∫ (x4/4)' log(x)2 dx =
x4/4·log(x)2 − ∫ x3/2·log(x) dx = (**)
∫ x3·log(x) dx = x4/4·log(x) − ∫ x3/4 dx
= x4/4·log(x) − x4/16 + c
(**) = x4/4·log(x)2 − x4/8·log(x) + x4/32 + c
(*) = e4/4 − e4/8 + e4/32 − 1/32 = (5e4 − 1)/32
Key Concepts [index]
⌠
⌡ |
f(x)g′(x) dx = f(x)g(x)- |
⌠
⌡ |
f′(x)g(x) dx. |
- Choose u, dv in such a way that:
- u is easy to differentiate – it is easy express f'(x).
- dv is easy to integrate – in "g'(x)" it is easy to see "g".
- ∫ v du is easier to compute that
∫ u dv.
- Sometimes it is necessary to integrate by parts more than once.
|
 x
x