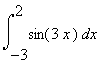 pongo u = 3x, ovvero x =u/3, du/dx = 3, dx = 1/3 du, 3·(-3)=-9, 3·2=6 Mi riconduco a:
pongo u = 3x, ovvero x =u/3, du/dx = 3, dx = 1/3 du, 3·(-3)=-9, 3·2=6 Mi riconduco a:
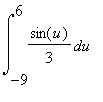 ossia a
ossia a 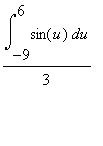 ...
...Lo Jacobiano (pronuncia "iacobiano")
1 Dalla derivata operando sostituzioni nell'integrazione univariata allo Jacobiano operando sostituzioni nell'integrazione bivariata
2 a Esempi di sostituzione nell'integrazione doppia (coord. polari)
b Esempi di sostituzione nell'integrazione tripla (coord. sferiche e cilindriche)
3 La matrice Jacobiana per esprimere il differenziale di una funzione di più variabili
(1) Una tecnica che si usa spesso nel calcolo di integrali è la sostituzione (cambiamento di variabili). Un esempio semplice come richiamo:
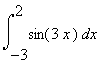 pongo u = 3x, ovvero x =u/3, du/dx = 3, dx = 1/3 du, 3·(-3)=-9, 3·2=6 Mi riconduco a:
pongo u = 3x, ovvero x =u/3, du/dx = 3, dx = 1/3 du, 3·(-3)=-9, 3·2=6 Mi riconduco a:
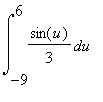 ossia a
ossia a 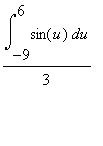 ...
...
In generale se pongo u = g(x), ovvero x = h(u), poiché D(h)(u) = dx / du,
ovvero, poiché il differenziale dx è uguale a D(h)(u) du, ho:
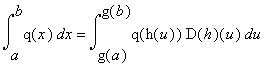 ovvero, se q(x) = f(g(x)):
ovvero, se q(x) = f(g(x)):
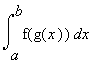 =
= 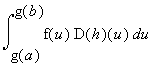
Nel caso degli integrali multipli il procedimento di cambiamento delle variabili è analogo:
l'integrale di F(x,y) per (x,y) in S
se pongo x = h1(u,v) e y = h2(u,v), ovvero u=g1(x,y), v=g2(x,y), diventa
l'integrale di F(h1(u,v), h2(u,v)) · |J(u,v)| per (u,v) in R trasformato di S mediante (g1,g2)
dove J(u,v) è la matrice, detta Jacobiana, delle derivate prime di h1 e h2:
![matrix([[diff(h1(u,v),u), diff(h1(u,v),v)], [diff(h2(u,v),u), diff(h2(u,v),v)]])](fpiuvar2/fpiuvar249.gif)
Tutto ciò si può fare se (h1,h2), ovvero (g1,g2), mettono in corrispondenza biunivoca R e S.
Il determinante della matrice Jacobiana viene chiamato anche lo Jacobiano (di h1 e h2).
In ulteriore analogia col caso univariato, dove abbiamo che du/dx = 1/(dx/du), qui abbiamo che:
|J(u,v)| = 1 / |J(x,y)|
In modo naturale il procedimento del cambio di variabili si estende agli integrali tripli.
(2)(a) Il cambiamento di variabili più comune è quello in coordinate polari (x=ρcos(θ), x=ρsin(θ)).
## Integrale su T = {(x,y) : x >=0, y <=0, x^2+y^2 <= 1} (parte nel 4° quadrante del cerchio di centro O e raggio 1) della funzione che a (x,y) associa x^3·y. Senza cambio di variabili:
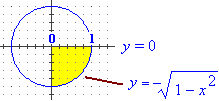
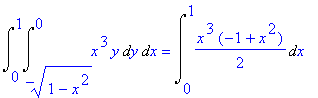 infatti:
infatti:
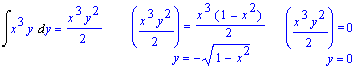
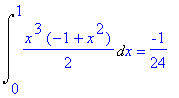 infatti:
infatti:
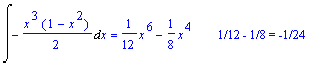
Rivediamolo usando questo cambiamento:
![]()
Le coordinate polari in questo caso sono comode per descrivere il dominio T:
0 <= ![]() <= 1, 3/2
<= 1, 3/2![]() <=
<= ![]() <= 2
<= 2![]()
Lo Jacobiano corrispondente a questo cambio di variabili è ρ; infatti:
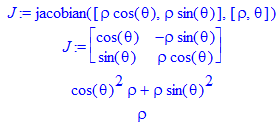
Quindi, l'integrale di f(x,y) per (x,y) in T
se pongo x = ![]() e y =
e y = ![]() diventa
diventa
l'integrale di ![]() per (
per (![]() ,
,![]() ) in [0, 1] x [3/2
) in [0, 1] x [3/2![]() , 2
, 2![]() ]
]
![]()
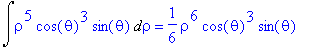
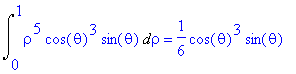
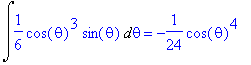
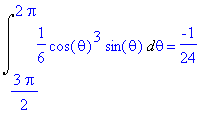
In breve:
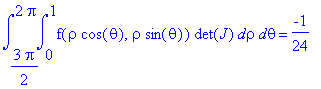
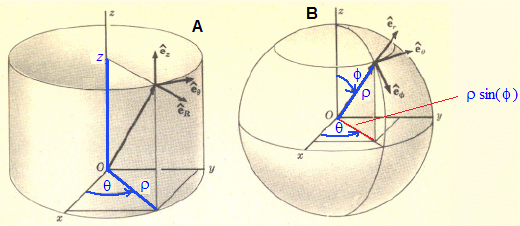
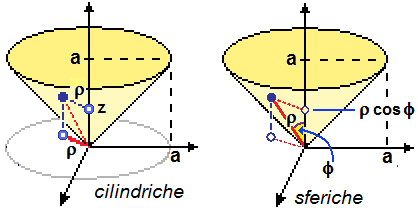
(b) Due frequenti cambi di coordinate nel caso degli integrali tripli:
l'impiego delle coordinate cilindriche (figura A, Jacobiano = ρ) e quello delle coordinate
sferiche (figura B, Jacobiano = ρ2sin(φ)):
 | |
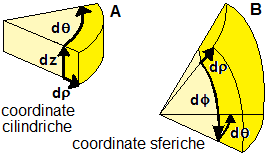 |
A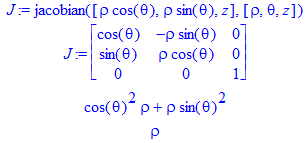 |
B | |
| Esempio Date le funzioni f(x,y,z) = z e g(x,y,z) = x2+y2+z2 e la regione R sopra
al cono z2 = x2+y2 e sotto al piano z = a, a > 0,
calcoliamo • Per il primo integrale usiamo le coordinate cilindriche: x = ρcosθ, y = ρsinθ, z = z. |J(ρ,θ,z)| = ρ. Il cono ha equazione z=ρ, per cui R è definibile mediante le condizioni 0 ≤ ρ ≤ a, ρ ≤ z ≤ a (e | 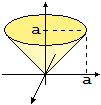 |
 | |
| Quindi ∫R z dxdydz =
∫[0,2π] ∫[0,a] ∫[ρ,a] z·ρ dzdρdθ =
| |
|
• Per il secondo integrale usiamo le coordinate sferiche (in quanto ci facilitano la descrizione di g):
x = Quindi | |
(3) La matrice Jacobiana ha in qualche modo assunto il ruolo che, per i cambiamenti di variabile nel caso univariato (x = h(u), dx = dh(u) = h'(u)du), aveva la derivata h'.
h'(u) du esprime il differenziale di h, ossia come varierebbe h(u) se u ha un incremento pari a du e se h proseguisse lineramente, ossia avesse per grafico la retta avente come pendenza quella che f ha nel punto u.
La Jacobiana, moltiplicata per il vettore degli N incrementi, esprime sotto forma di matrice il differenziale di una funzione f di N variabili.
Nel caso N=1, e 1 output, ritroviamo il differenziale a noi già noto:
![]()
![]()
| J×H |
![]()
Nel caso N=1 e 2 output abbiamo:
![J := matrix([[diff(f(x),x)], [diff(g(x),x)]])](fpiuvar2/fpiuvar274.gif)
![]()
| J × H |
![matrix([[diff(f(x),x)·h], [diff(g(x),x)·h]])](fpiuvar2/fpiuvar276.gif)
Nel caso N=2 e 1 output il differenziale è, analogamente al caso N=1, la variazione che (al variare di x di dx=h e di y di dy=k) avrebbe f(x,y) se proseguisse lineramente, ossia avendo come grafico il piano tangente alla superficie z=f(x,y) nel punto (x,y):
df(x,y) = df(x,y)/dx · h + df(x,y)/dy · k
(il piano tangente in P=(x,y) è P + df(x,y)/dx · h + df(x,y)/dy · k al variare di h e k in R).
Se h=cos(θ) e k=sin(θ), df(x,y)/dx · h + df(x,y)/dy · k è la derivata direzionale nella direzione θ, ossia nella direzione del versore (h,k)
![]()
![H := matrix([[h], [k]])](fpiuvar2/fpiuvar281.gif)
| J × H |
![]()
[Se f è a 1 output, ossia se f è un campo scalare, la matrice Jacobiana coincide con il gradiente di f]
Nel caso N=2 e 2 output (ossia il caso del cambiamento di variabili per gli integrali doppi) abbiamo:
![J := matrix([[diff(f(x,y),x), diff(f(x,y),y)], [diff(g(x,y),x), diff(g(x,y),y)]])](fpiuvar2/fpiuvar283.gif)
![H := matrix([[h], [k]])](fpiuvar2/fpiuvar284.gif)
| J × H |
![matrix([[diff(f(x,y),x)·h+diff(f(x,y),y)·k], [diff(g(x,y),x)·h+diff(g(x,y),y)·k]])](fpiuvar2/fpiuvar285.gif)
Per dare una interpretazione geometrica in questo caso, in cui (f,g) rappresenta una trasformazione da R^2 in R^2, si dimostra che il det. della matrice Jacob. è positivo quando la trasformazione conserva il senso delle rotazioni: una curva percorsa in verso orario viene percorsa allo stesso modo nel piano trasformato mediante (f,g). Lo Jacobiano vale 1 o -1 nel caso delle isometrie (traslazioni, rotazioni, simmetrie e loro composizioni).
Nota 1: date u = u(x,y) e v = v(x,y), per indicare lo Jacobiano si ricorre anche alla notazione:
Nota 2:
| ∂(u, v) / ∂(x, y) = | | | | | |
∂u/∂x | ∂u/∂y | | | | | |
= | | | | | |
∂u/∂x | ∂v/∂x | | | | | |
in quanto det(At) = det(A) | ||||||
| ∂v/∂x | ∂v/∂y | ∂u/∂y | ∂v/∂y |