Limit Definition of the Derivative

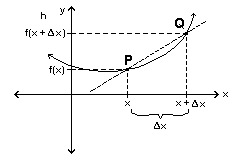
The geometric meaning of the derivative

f′(x) = d
dx		f(x)
is the slope of the line tangent to y = f(x) at x.

Let's look for this slope at P:

The secant line through P and Q has slope

f(x+Δx)-f(x)
(x+Δx)-x
 = f(x+Δx)-f(x)
Δx
 .
Figure 1

We can approximate the tangent line through P by moving Q towards P, decreasing Δx. In the limit as Δx→ 0, we get the tangent line through P with slope


lim
Δx→ 0 
 f(x+Δx)-f(x)
Δx
 .

We define

f′(x) =
lim
Δx→ 0 
 f(x+Δx)-f(x)
Δx
 .
If the limit as Δx → 0 at a particular point does not exist, f′(x) is undefined at that point.

We derive all the basic differentiation formulas using this definition.

Example

For f(x) = x2,

f′(x)
=

lim
Δx→ 0 
 (x+Δx)2-x2
Δx
=

lim
Δx→ 0 
 (x2+2(Δx)x+Δx2)-x2
Δx
=

lim
Δx→ 0 
 2(Δx)x+Δx2
Δx
=

lim
Δx→ 0 
 (2x+Δx)
=   2x
as expected.

Example

For f(x) = 1/x

f′(x)
=

lim
Δx→ 0 
1
x+Δx
 - 1
x
Δx
=

lim
Δx→ 0 
x-(x+Δx)
(x+Δx)(x)
Δx
=

lim
Δx→ 0 
-Δx
(x+Δx)(x)
Δx
=

lim
Δx→ 0 
 -1
(x+Δx)(x)
=
- 1
x2
again as expected.

Notes

The limit definition of the derivative is used to prove many well-known results, including the following:

  • If f is differentiable at x0, then f is continuous at x0. [ma sarebbe più sensato definire la derivata direttamente solo per le funzioni continue]

  • Differentiation of polynomials.

  • Product and Quotient Rules for differentiation.

Si usano anche altre notazioni:
•  D(f) al posto di f'
•  D(f)(x)  o  Dx((f(x))  o  (f(x))'x   al posto di f'(x)
Key Concepts [index]

We define

f′(x) =
lim
Δx→ 0 
 f(x+Δx)-f(x)
Δx
 .