Computing Limits

Intuitively, we say that limx→ c f(x) = L if f is defined near (but not necessarily at) c and f(x) approaches L as x approaches c.

If we let x approach c from the left side only, we write limx→ c- f(x) since x is approaching c from smaller values. Similarly, for x approaching c from the right, we write limx→ c+ f(x). The two-sided limit limx→ c f(x) exists if and only if both of these one-sided limits exist and they are equal.

An Intuitive Example

Consider the graph of a function f(x) shown below.

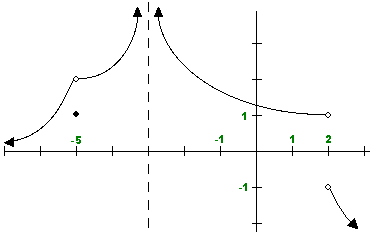
Evaluate each of the following. Select (click) each one to check your reasoning.

•   f(2)
          •   f(-5)
          •  
lim
x→ -3 
 		f(x)
•  
lim
x→2+ 
 		f(x)
          •  
lim
x→-5+ 
 		f(x)
          •  
lim
x→ - ∞ 
 		f(x)
•  
lim
x→2- 
 		f(x)
          •  
lim
x→-5- 
 		f(x)
          •  
lim
x→ ∞ 
 		f(x)
•  
lim
x→ 2 
 		f(x)
          •  
lim
x→ -5 
 		f(x)
          •  
lim
x→c 
 		f(x)  for  c ≠ -5, -3, 2.

Definition of the Limit

More rigorously, let f be defined at all x in an open interval containing c, except possibly at c itself.

Then


lim
x→ c 
 f(x) = L
if and only if for each ε > 0, there exists a δ > 0 such that
if  0 < |x-c| < δ then  |f(x)-L| < ε.

In words, limx→ c f(x) = L if and only if by taking x close enough to c (but different from c: see c = −5 in the preceding example) we can get f(x) arbitrarily close to L.

animazione

Properties of the Limit

Each of the following properties is proven using the rigorous definition of the limit. Let lim stand for limx→ c, limx→ c+, or limx→ c-. Assume lim f(x) and lim g(x) both exist.

  • (Uniqueness)   If lim f(x) = L1 and lim f(x) = L2, then L1 = L2.
  • (Addition)   lim [f(x)+g(x)] = lim f(x) +lim g(x).
  • (Scalar multiplication)   lim [αf(x)] = αlim f(x).
  • (Multiplication)   lim [f(x)g(x)] = lim f(x) · lim g(x).
  • (Division)   lim [f(x)/ g(x)] = lim f(x) / lim g(x), provided lim g(x) ≠ 0.
  • (Powers)   lim [f(x)]n = [lim f(x)]n for any positive integer n.

In practice, much of the time we can ``reason out'' the value of a limit without explicitly using the ε-δ definition.

Examples

  • limx→ 2 √(x2+12) = 4 since the function f(x) = √(x2+12) is continuous at x = 2 and f(2) = 4.
  • limx→ ∞ 1/x = 0 since as x increases, 1/x gets arbitrarily close to 0.
  • limx→ 0+ ln|x| tends to -∞ and so does not exist since as x decreases to 0, ln|x| gets arbitrarily large in magnitude and negative.
  • limx→ 3 [(x2-9)/( x-3)] = 6 even though f(x) = (x2-9)/( x-3) is undefined at x = 3 since (x2-9)/( x-3) = x+3 and limx→ 3x+3 = 6.

What about something like limx→ 0 [sin x / x]? When we cannot easily ``reason out'' the value of a limit, we can often use numerical methods or L'Hôpital's Rule to determine the value of the limit. Can you convince yourself that limx→ 0 [sin x / x] = 1?


Key Concepts [index]

  • Let the function f be defined at all x in an open interval containing c, except possibly at c itself.

    Then


    lim
    x→ c 
    		 f(x) = L
    if and only if for each ε > 0, there exists a δ > 0 such that
    if  0 < |x-c | < δ then  |f(x)-L| < ε.

    In words, the limit of f(x) as x approaches c is L if and only if by taking x close enough to c (but different from c) we can get f(x) arbitrarily close to L.