|
Geometry of Linear Transformations of the Plane (and the Space)
Let V and W be vector spaces. Recall that a function T:V→ W is called a linear transformation if it preserves
both vector addition and scalar multiplication:
for all v1, v2 ∈ V.
Se V = R2, W = R2 e T:R2 → R2 è una trasformazione lineare,
se i e j sono, in ordine, i versori dell'asse x e del'asse y, dato il vettore v, esso è scomponibile come xi+yj,
per cui
T(v) = T(xi+yj) = xT(i)+yT(j) = xi'+yj', dove abbiamo
indicato con i' e j'
i trasformati dei versori. Quindi T è individuata dai vettori i' e j',
che possiamo rappresentare, mettendoli in colonna, con una matrice A 2×2. i'x+j'y possiamo allora
interpretarla come l'espressione delle due righe della matrice che si ottiene moltiplicando A per il vettore colonna (x,y).
Then, if V = R2 and W = R2, then T:R2 → R2 is a
linear transformation if and only if there exists a 2 ×2
matrix A such that T(v) = Av for all v ∈ R2. Matrix A is called the standard matrix for T. The
columns of A are T( [ 1 0 ]T) and
T( [ 0 1 ]T), respectively. Since
each linear transformation of the plane has a unique standard matrix,
we will identify linear transformations of the plane by their standard
matrices. It can be shown that if A is invertible, then the linear
transformation defined by A maps parallelograms to parallelograms.
We will often illustrate the action of a linear transformation T:R2→ R2 by looking at the image of a unit square under T.
Rotations
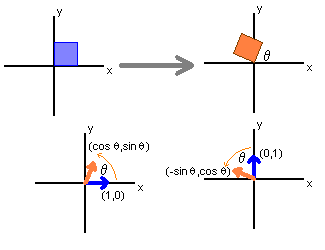
The standard matrix for the linear transformation T:R2 →R2 that rotates vectors by an angle θ is
This is easily derived by noting that
|
|
|
T |
/
|
|
\ |
|
/
|
\ |
|
1
0
|
\
|
/ |
\
|
|
/ |
|
|
|
|
|
T |
/
|
|
\ |
|
/
|
\ |
|
0
1
|
\
|
/ |
\
|
|
/ |
|
|
|
|
| |
|
Nota. Se compongo una rotazione di α e una rotazione di β la rotazione complessiva è
associata alla matrice
/ cosβ -sinβ \ / cosα -sinα \ / cosβ cosα - sinβ sinα -cosβ sinα - sinβ cosα \
| | × | | = | |
\ sinβ cosβ / \ sinα cosα / \ sinβ cosα + cosβ sinα -sinβ sinα + cosβ cosα /
che deve coincidere con
/ cos(α+β) -sin(α+β) \
| |
\ sin(α+β) cos(α+β) /
Ritroviamo così che cos(α+β) = cosβ cosα - sinβ sinα
e che sin(a+ß) = sinβ cosα + cosβ sinα
Reflections
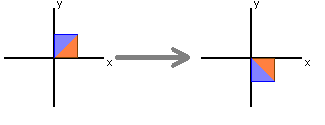
For every line in the plane, there is a linear transformation that
reflects vectors about that line. Reflection about the x-axis is
given by the standard matrix
which takes the vector [ x y ]T to [ x -y ]T. Reflection about the y-axis is given by the standard matrix
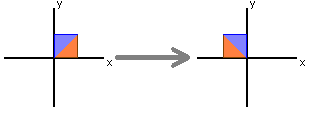 taking [ x y ]T to [ -x y ]T.
Finally, reflection about the line y = x is given by
taking [ x y ]T to [ -x y ]T.
Finally, reflection about the line y = x is given by
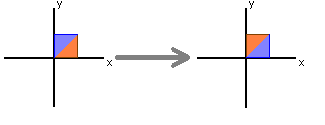 and takes the vector [ x y ]T to [ y x ]T.
and takes the vector [ x y ]T to [ y x ]T.
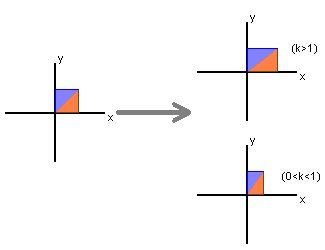
Expansions and Compressions
The standard matrix
``stretches'' the vector [ x y ]T along the
x-axis to [ kx y]T for k > 1 and
``compresses'' it along the x-axis for 0 < k < 1.
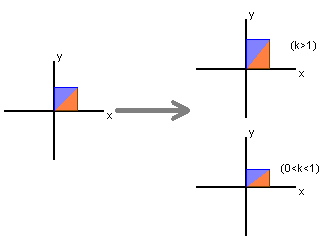 Similarly,
stretches or compresses vectors [ x y ]T to
[ x ky ]T along the y-axis.
Similarly,
stretches or compresses vectors [ x y ]T to
[ x ky ]T along the y-axis.
Shears
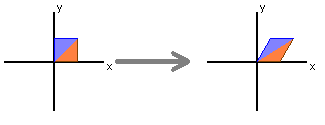
The standard matrix
taking vectors [ x y ]T to [ (x+ky) y ]T is called a shear in the x-direction.
k = ? → 
Similarly,
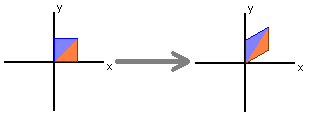 takes vectors [ x y ]T to [ x (y+kx) ]T and is called a shear in the y-direction.
takes vectors [ x y ]T to [ x (y+kx) ]T and is called a shear in the y-direction.
Notes
- If finitely many linear transformations from R2 to R2 are performed in succession, then there exists a single linear
transformation with the same effect.
- If the standard matrix for a transformation T: R2→ R2 is invertible, then it can be shown that the
geometric effect of T is the same as some sequence of reflections,
expansions, compressions, and sheers.
In the following Exploration, you can investigate the connection
between the entries in a standard matrix and the effect the
corresponding linear transformation has geometrically.
Exploration
In the Space
Quanto visto per R2 può essere esteso a R3.
Ad esempio la matrice per la trasformazione lineare T:R3 →R3
che ruota i vettori di un angolo θ attorno all'asse z è
infatti:
|
| T |
/
|
|
|
\ |
|
/
|
|
\ |
| 1
0
0
|
\
|
|
/ |
\
|
|
|
/ |
|
|
|
|
/
|
|
\ |
| cos θ
sin θ
0
|
\
|
|
/ |
|
|
| T |
/
|
|
|
\ |
|
/
|
|
\ |
| 0
1
0
|
\
|
|
/ |
\
|
|
|
/ |
|
|
|
|
/
|
|
\ |
|
-sin θ
cos θ
0
|
\
|
|
/ |
|
|
| T |
/
|
|
|
\ |
|
/
|
|
\ |
|
0
0
1
|
\
|
|
/ |
\
|
|
|
/ |
|
|
|
|
| | |
Analoga è la descrizione della rotazione attorno ad uno degli altri assi.
Consideriamo, invece, il caso di un generico
movimento che mantiene fissa l'origine. Supponiamo di conoscere come vengono trasformati i versori degli assi.
Vediamo per semplicità prima il caso piano, che in realtà non presenta novità rispetto alla
situazione considerata all'inizio.
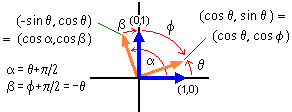
Se cos(θ) e cos(φ) sono i coseni direttori del trasformato dell'asse x (ovvero le componenti del trasformato del versore i) e cos(α) e cos(β) sono quelli del trasformato dell'asse y (le componenti
del trasformato di j), possiamo descrivere la rotazione così:
| A = |
/
|
|
\ |
| |
\
|
|
/ |
|
= |
/
|
|
\ |
|
|
\
|
|
/ |
|
|
in quanto:
|
| T |
/
|
|
\ |
|
/
|
\ |
| 1
0
|
\
|
/ |
\
|
|
/ |
|
|
|
|
| T |
/
|
|
\ |
|
/
|
\ |
0
1
|
\
|
/ |
\
|
|
/ |
|
| |
|
| |
|
Naturalmente, tenendo conto delle relazioni tra θ, φ, α e β, possiamo poi ricondurci alla matrice vista all'inizio.
Nel caso tridimensionale abbiamo, in modo del tutto analogo:
| A = |
/
|
|
|
|
\ |
| |
\
|
|
|
|
/ |
|
|
che può essere semplificata in vari modi, tenendo conto delle relazioni che intercorrono tra i vari coseni direttori
in conseguenza della relazione di perpendicolarità che intercorre tra i trasformati degli assi.
Nel caso si sappia descrivere questo movimento come rotazione di un angolo θ attorno a una certa retta, si può
rappresentare la trasformazione operando un cambio di base che trasformi questa retta nell'asse z e riconducendosi
alla matrice descritta poco sopra. Si veda la sezione "cambiamento di base".
Nucleo di una trasformazione lineare
Per verificare se una trasformazione lineare F da V in W è iniettiva (ossia trasforma input diversi in output diversi)
basta verificare che F(v) = 0 solo se v = 0 (qui con 0 indichiamo il vettore nullo); infatti, se vale questa proprietà, da
F(v1) = F(v2), che equivale a F(v1) - F(v2) = 0, ossia (per la linearità) a F(v1 - v2) = 0,
si deduce v1 - v2 = 0, ossia v1 = v2.
Chiamando nucelo (kernel) di F, e indicando con ker(F), la controimmagine di {0}, ossia {v in V / F(v) = 0},
possiamo dire che F è iniettiva sse ker(F) = {0}.
Se V e W sono due spazi della stessa dimensione finita
(ad es. entrambi uguali a R2 o a R3) e F è
iniettiva allora F è anche bigettiva, ossia Im(F), cioè F(V),
coincide con W, e questo equivale alla invertibilità della matrice A associata ad F.
È facile dimostrare che ker(F) e Im(F) sono sottospazi vettoriali (di V e W),
e che dim(ker(F)) + dim(Im(F)) = dim(V).
Se V e W sono di dimensione finita, dim(Im(F)) coincide col rango ρ(A) della matrice A associata ad F.
Ad es. la matrice A avente per righe [12,1,0], [8,10,0], [1,3,0] è associata ad
F: R3 → R3 che ha per Im(F) il piano generato dai vettori (12,8,1) (=A×[1,0,0]T) e (1,10,3)
(=A×[0,1,0]T), che sono 2 [2 = ρ(A)] colonne indipendenti di A.
Per ker(F) ha l'asse z, generato, per es., dal vettore (0,0,1). Infatti A×[x,y,z]T = [0,0,0]T
ha come soluzioni x=0, y=0, z qualunque. |
Trasformando una matrice in forma triangolare alta (o, in particolare, diagonale)
evidentemente il nucleo non cambia. Nel caso, evidente, della A a fianco, triangoliamo e ci riconduciamo
a risolvere:
12x = 0 & -14y = 0, che ha come soluzioni x=0, y=0, z qualunque. Il nucleo è generato da (0,0,1).
|
/12 1 0\ /12 1 0\ /12 0 0\
| 8 10 0| | 0 -14 0| | 0 -14 0|
\ 1 3 0/ \ 0 14 0/ \ 0 0 0/ |
| Durante la trasformazione le relazioni di dipendenza tra le colonne si
mantengono per cui le colonne che formerebbero una base dell'immagine nel caso che la matrice fosse quella finale,
ossia la 1ª e la 2ª,
corrispondono alle colonne che formano una base dell'immagine della trasformazione associata alla matrice iniziale: ritroviamo che come base
possiamo prendere (12,8,1) e (1,10,3). Ovviamente queste considerazioni possono tornare utili nel caso di matrici più complesse, e di dimensione maggiore,
rispetto al caso, banale, qui esemplificato.
|
Key Concept [index]
For every linear transformation T: R2 → R2 of the plane,
there exists a standard matrix A such that
|
T(v) = Av for all v ∈ R2. |
|
Every linear transformation of the plane with an invertible
standard matrix has the geometric effect of a sequence of reflections,
expansions, compressions, and shears.
|

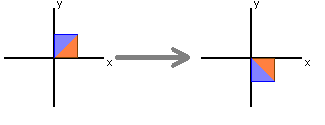

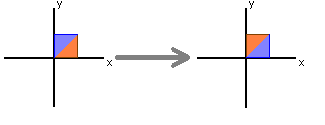 and takes the vector [ x y ]T to [ y x ]T.
and takes the vector [ x y ]T to [ y x ]T.

 Similarly,
Similarly,
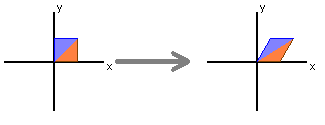
 takes vectors [ x y ]T to [ x (y+kx) ]T and is called a shear in the y-direction.
takes vectors [ x y ]T to [ x (y+kx) ]T and is called a shear in the y-direction.

