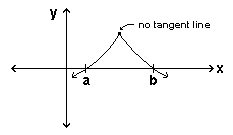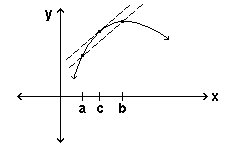|
somewhere between two zeros of a non-constant continuous function f, the function must change direction
Rolle's Theorem Let f be differentiable on (a,b) and continuous on [a,b]. If f(a) = f(b) = 0, then there is at least one point c in (a,b) for which f ′(c) = 0.
Notice that both conditions on f are necessary. Without either one,
the statement is false!
Though the theorem seems logical, we cannot be sure that it is always true without a proof.
The Mean Value Theorem is a generalization of Rolle's Theorem: We now let f(a) and f(b) have values other than 0 and look at the secant line through (a, f(a)) and (b, f(b)). We expect that somewhere between a and b there is a point c where the tangent is parallel to this secant.
That is, the slopes of these two lines are equal. This is formalized in the Mean Value Theorem. Mean Value Theorem for derivatives (or Lagrange's Theorem) Let f be differentiable on (a,b) and continuous on [a,b]. Then there is at least one point c in (a,b) for which
Here, f ′(c) is the slope of the tangent at c, while (f(b)-f(a))/( b-a) is the slope of the secant through a and b. Intuitively, we see that if we translate the secant line in the figure upwards, it will eventually just touch the curve at the single point c and will be tangent at c. However, basing conclusions on a single example can be disastrous, so we need a proof.
Consequences of the Mean Value Theorem The Mean Value Theorem is behind many of the important results in calculus. The following statements, in which we assume f is differentiable on an open interval I, are consequences of the Mean Value Theorem:
Mean Value Theorem Let f be differentiable on (a,b) and continuous on [a,b]. Then there is at least one point c in (a,b) for which
|
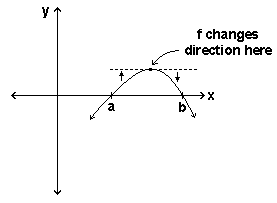 We begin with a common-sense geometrical fact:
We begin with a common-sense geometrical fact: