Recall our definition of the definite integral of a function of a single variable:

Let f(x) be defined on [a,b] and let x₀,x₁,…,x_n be a partition of [a,b]. For each [x_i-1,x_i], let x_i^* ∈ [x_i-1,x_i]. Then

∫ b a  f(x) dx = lim maxΔxi → 0  n Σ i = 1  f(xi*)Δxi

Take a quick look at the Riemann Sum Tutorial

We can extend this definition to define the integral of a function of two or more variables.

Double Integral of a Function of Two Variables (sia R una regione piana contenuta in una regione rettangolare W; se W è suddivisa in rettangolini mediante rette orizzontali e verticali, l'insieme di tutti i rettangolini contenuti completamente in R viene chiamato partizione interna di R) Let f be defined on a closed and bounded region R of the xy-plane. Set up a grid of vertical and horizontal lines in the xy-plane to form an inner partition of R into n rectangular subregions Rk of area ΔAk, each of which lies entirely in R (ignore the rectangles that are not entirely contained in R). Choose a point (xk*, yk*) in each subregion Rk. The sum n Σ k = 1  f(xk*, yk*) ΔAk       is called a Riemann Sum.  In the limit as we make our grid more and more dense, we define the double integral of f(x,y) over R as

• If this limit exists, we say that f is integrable over the region of integration R.

• If f is continuous on R, then f is integrable over R.

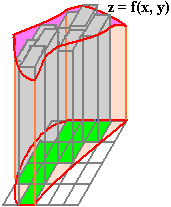
Geometric Interpretation of the Double Integral

Notice that as we increase the density of our grid, the sum Σ_kA_k of the individual rectangles better and better approximates the area of region R. In the limit as ΔA_k → 0, we have

The interpretaion of the double integral as a volume still holds if f(x,y) takes on both positive and negative values. In this case, we obtain the difference between the volume above the xy-plane between z = f(x,y) and R and the volume below the xy-plane between z = f(x,y) and R.

We next turn to the actual evaluation of double integrals.

Iterated Integrals

In the double integral

∫∫ R

f(x,y) dA, dA may be viewed informally as an infinitesimal

area of a rectangle inside R with dimensions dy and dx. For the kinds of "ordinary" functions and regions we'll be concerned with,

∫∫ R f(x,y) dA = ∫ b a  ∫ g2(x) g1(x)  f(x,y) dy dx = ∫ b a  ∫ g2(x) g1(x)  f(x,y) dy dx = ∫ d c  ∫ h2(y) h1(y)  f(x,y) dx dy = ∫ d c  ∫ h2(y) h1(y)  f(x,y) dx dy

where the limits of integration are determined by the region R over which we are integrating.

These integrals are called iterated integrals, since we integrate more than once.

	We integrate "from the inside out". That is, in ∫	b a	∫	g2(x) g1(x)	f(x,y) dy dx, we first integrate
	f(x,y) with respect to y and evaluate it at g2(x) and g1(x). We then integrate the result with respect to x and evaluate the outcome at a and b.

Iterated triple integrals

∫∫∫ G

f(x,y,z)dV can be defined in a similar way.

An example will make these ideas more concrete.

Example

Let's evaluate the double integral

∫∫ R

6xy dA, where R is the region bounded by

y = 0, x = 2, and y = x². We will verify here that the order of integration is unimportant:

∫∫ R 6xy dA = ∫ 2 0  ∫ x2 0  6xy dy dx = ∫ 2 0  [ 3xy2 |y = 0x2 ] dx = ∫ 2 0  3x5 dx = 1 2 x6 | | | 2 x = 0  = 1 2 (64)- 1 2 (0) = 32

∫∫ R 6xy dA = ∫ 4 0  ∫ 2 √y  6xy dx dy = ∫ 4 0  [ 3x2y |x = √y2 ] dy = ∫ 4 0  ( 12y-3y2 ) dy = ( 6y2 -y3 ) |4y = 0 = ( 6(4)2-43 ) - ( 6(0)2- 03 ) = 32

so

∫∫ R

6xy dA = 32 here, regardless of the order in which we carry out

the integration, as long as we are careful to set up the limits of integration correctly.

Now for a triple integral...

Example

We will evaluate the triple integral ∫

2 0

∫

y2 -1

∫

z 1

yz dx dz dy.

∫ 2 0  ∫ y2 -1  ∫ z 1  yz dx dz dy = ∫ 2 0  ∫ y2 -1  [ (xyz) |x = 1z ] dz dy Integrate with respect to x first. = ∫ 2 0  ∫ y2 -1  ( yz2-yz ) dz dy Next integrate with respect to z. = ∫ 2 0  yz3 3 - yz2 2 | | | y2 z = -1  dy = ∫ 2 0  y7 3 - y5 2 + 5y 6 dy Finally, integrate with respect to y. = y8 24 - y6 12 + 5y2 12 | | | 2 0  = 264 24 - 64 12 + 20 12 = 84 12 = 7

Let f(x,y) be defined on a closed and bouned region R of the xy-plane. Then

We evaluate

∫∫ R

f(x,y) dA as an iterated integral: