Modelli differenziali
La matematizzazione di una situazione problematica sotto forma di un sistema di equazioni o disequazioni in cui compaiano derivate (prime, seconde o di altro ordine) di una o più variabili funzionali viene chiamato modello differenziale.
• Un semplice esempio è costituito dalla singola equazione differenziale  s'(t) = 5  che, se interpretiamo s come la funzione che associa all'istante t (avendo assunto un certo istante come tempo 0 e fissato una certa unità di tempo UT) la posizione s(t) che un certo corpo ha lungo una data traiettoria (avendo assunto un certo punto come posizione 0 e fissato una certa unità di lunghezza UL), esprime il fatto che quel corpo sta viaggiando con una velocità costante pari a 5 (UL/UT).
Risolvere questa equazione rispetto a s vuol dire trovare tutte le funzioni s la cui derivata sia 5, ossia determinare l'integrale indefinito di s, ossia  s(t) = 5t+C  al variare di C in R.
Se aggiungo all'equazione  s'(t) = 5  l'ulteriore equazione (questa non differenziale)  s(3) = 7  (all'istante 3 il corpo ha la posizione 7) ottengo un sistema che, in questo caso ha, risolto rispetto a s, un'unica soluzione:  da  5·3+C = 7  ricavo C = 15-7 = 8, ossia s(t) = 5t+8.
• Un altro esempio è costituito dalla equazione differenziale  s"(t) = 5  che, con la stessa interpretazione data sopra, esprime il fatto che il corpo sta viaggiando con una accelerazione costante pari a 5 (UL/UT²).
Le soluzioni sono tutte le funzioni s la cui derivata seconda sia 5. Se indico con v la funzione s', l'equazione diventa v'(t) = 5 che ha come soluzioni v(t) = 5t+C  al variare di C in R. A loro volta ciascuna di queste equazioni, ossia s'(t) = 5t+C, ha come soluzioni s(t) = 5t²/2+Ct+C' al variare di C' in R. In definitiva l'equazione differenziale ha come soluzioni:  s(t) = 5t²/2+Ct+C'  al variare di C e di C' in R.
In questo caso per avere un'unica soluzione posso imporre una condizione sulla velocità in un certo istante oltre che una sulla posizione. Se ad esempio impongo che v(4) = 5, ossia s'(4) = 5·4+C = 5, ricavo C = -15; se impongo inoltre che s(2) = 10, ossia 5·2²/2-15·2+C' = 10, ricavo C' = 30, ossia s(t) = 5t²/2-15t+30.
• Un altro esempio. Quali sono le funzioni che hanno come derivata sé stesse. A questo problema corrisponde il modello differenziale  f'(x)=f(x).  Noi sappiamo che una soluzione di questa equazione è f = exp. Infatti D(exp) = exp. Ma, ricordando che, se C è una costante numerica, D(Cf) = CD(f), capiamo che sono soluzioni anche tutte le funzioni f(x) = C·exp(x); infatti D_x(C·exp(x)) = C·D_x(exp(x)) = C·exp(x).
• Quando non ci riferisce a un particolare contesto, è molto spesso usata la convenzione di considerare x come variabile di input della funzione incognita φ e di indicare con y il termine φ(x). Le equazioni differenziali considerate sopra (s'(x)=5, s"(x)=5, s'(x)=5x+C, f'(x)=f(x)) verrebbero ad esempio scritte, rispettivamente, nei seguenti modi:
        y' = 5       y" = 5       y' = 5x+C       y' = y.
Altre volte si prende come variabile di input t. Con questa convenzione le stesse equazioni diventerebbero:
        y' = 5       y" = 5       y' = 5t+C       y' = y.
Altre volte si prende come variabile di input t e si indica il valore della funzione incognita con x. Con questa convenzione le stesse equazioni diventerebbero:
        x' = 5       x" = 5       x' = 5t+C       x' = x.
Esistono anche altre convenzioni. Dal contesto sono in genere comprensibili.
• La seconda equazione è chiamata del "secondo ordine" in quanto in essa compare la derivata seconda dell'incognita; le altre sono equazioni differenziali del "primo ordine" in quanto al più compare la derivata prima. La terza equazione ha la forma F(y',x)=0, la quarta ha la forma F(y',y)=0 ma vi possono essere equazioni differenziali del primo ordine del tipo F(y',y,x)=0, ossia in cui compiaono sia y' che y ed x.
Sotto sono raffigurati i "campi direzionali" delle soluzioni di y'=5x e y'=y: per un po' di punti sono stati tracciati i segmentini che passano per il punto e che hanno come pendenza y': in ogni punto (x,y) nel primo caso la pendenza è 5x, ossia dipende solo da x; nel secondo caso è y, ossia dipende solo da y.
L'insieme dei segmentini dà l'idea dell'andamento delle soluzioni dell'equazione. Nel primo caso si tratta di curve ottenibili l'una dall'altra mediante una traslazione verticale, nel secondo abbiamo due famiglie di curve, ciascuna composta da curve ottenibili l'una dall'altra mediante traslazioni orizzontali: quelle superiori sono del tipo y = C·exp(x), ovvero y = exp(x+log(C)), con C>0, quelle inferiori con C<0 [y = -exp(x+log(|C|)]; poi c'è l'asse x.
In entrambi i casi, fissato un punto del piano (x, y) esiste una unica curva soluzione che passa per esso, ossia un'unica soluzione y=f(x) tale che f(x) = y.
Vedremo che questo non si verifica con tutte le equazioni differenziali del primo ordine.

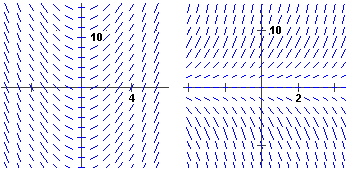
dy/dx = 5x                       dy/dx = y
Qui trovi come tracciare (con R) i campi direzionali delle eq. differenziali del 1º ordine.

Equazioni differenziali del primo ordine
Consider the first-order ODE

1. Does y ′ = f(t,y), y(t₀) = y₀ have a solution?

2. If so, can we find a formula for the solution?

Suppose that f(t,y) and (∂f(t,y))/( ∂y) are continuous on a closed rectangle R of the ty-plane. If (t₀,y₀) ∈ R, then the IVP

In quali dei seguenti casi vi sono (x₀,y₀) per i quali non passa un'unica curva soluzione di y'=f(x,y)?  [x e y variano tra -4 e 4]

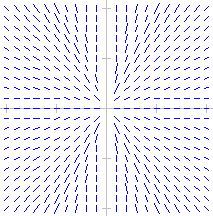
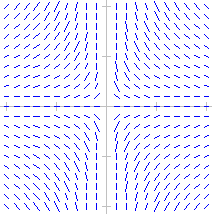
y'x = y  (y' = y/x)	y'x = -y  (y' = -y/x)
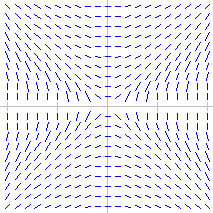
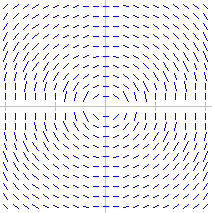
y'y = x  (y' = x/y)	y'y = -x  (y' = -x/y)
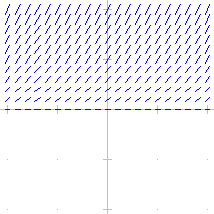
y' = √y	y' = 1+x/(y2+1)

The second question is much more difficult, and often we need to resort to numerical methods. However, in this tutorial we review four of the most commonly-used analytic solution methods for first-order ODES.

Separating the Variables

Esempio introduttivo:
y' = y,  ossia  dy/dt = y.   Posso mettere da una parte le y e dall'altra le t.
Scrivo:  dy /y = dt. Ma così perdo la soluzione y = 0: me lo annoto.
"Integro" i due membri:  ∫ dy/y = ∫ dt.  Ottengo:  log(y) = t + C1, log(-y) = t + C2
Applico exp:  y = exp(t+C), y = -exp(t+C)
Queste soluzioni volendo posso riscriverle così:
y = exp(C)exp(t), y = -exp(C)exp(t), ovvero: y = C·exp(t), y = -C·exp(t), con C>0,
ovvero, unificandole: y = C·exp(t) con C numero reale qualunque; per C=0 recupero la soluzione che avevo perso "portando" y dalla parte di y'.
La soluzioni trovate sono in accordo con quanto visto nel paragrafo introduttivo.
Trattazione generale: 

If an ODE can be written in the form

       Suppose y = f(t) solves the ODE. Rewriting the ODE as h(y)y ′ = g(t),

h(f(t))f ′(t)	=	g(t)	since y = f(t), y ′ = f ′(t)
∫h(f(t))f ′(t)dt	=	∫g(t)dt +C	Integrating with respect to t on each side.
∫h(y)dy	=	∫g(t)dt +C	since dy = f ′(t)dt

Upon integrating, we have our implicitly-defined general solution of the ODE, which we can often solve explicitly for y(t).

Example

Let's solve the separable ODE y ′ = 4y/t. Separating the variables and integrating,

The general solution, y = ct⁴, defines a family of solution curves corresponding to various initial conditions.

Using an Integrating Factor to solve a Linear ODE

If a first-order ODE can be written in the normal linear form

μ(t)[ y ′+ p(t)y ] = μ(t)q(t)	Multiplying both sides of the ODE by μ(t).
( μ(t)y )  ′ = μ(t)q(t)	( μ(t)y )  ′ = μ(t)y ′+ μ ′(t)y and μ ′(t) = p(t) μ(t) using the chain rule to differentiate μ(t) = e∫p(t)dt.
μ(t)y = ∫ μ(t)q(t) dt + C	Integrating each side with respect to t.

Dividing through by μ(t), we have the general solution of the linear ODE.

Example

We can solve the linear ODE  y ′-2ty = t  using an integrating factor. Here, p(t) = -2t and q(t) = 1, so

You can verify that (e^-t2y) ′ = e^-t2(y ′-2ty) by using the Chain Rule to differentiate e^-t2y Integrating each side with respect to t. Dividing through by e^-t2.

So the general solution of y ′-2ty = t is y(t) = Ce^t2-¹/₂.

For practice, solve y ′ = [4y/ t] by putting it in normal linear form and using an integrating factor. Verify that you get the same result as we did by separating the variables.

Using a Change of Variables

Often, a first-order ODE that is neither separable nor linear can be simplified to one of these types by making a change of variables. Here are some important examples:

• Homogenous Equation of Order 0: [dy/ dx] = f(x,y) where f(kx,ky) = f(x,y).

  Use the change of variables z = ^y/_x to convert the ODE to x[dz/ dx] = f(1,z)-z, which is separable.

• Bernoulli Equation: [dy/ dt]+p(t)y = q(t)y^b    (b ≠ 0,1).

  Use the change of variables z = y^1-b to convert the ODE to [dx/ dt] + (1-b)p(t)z = (1-b)q(t), which is linear.

• Riccati Equation: [dy/ dt] = a(t)y+b(t)y²+ F(t).

  If one particular solution g(t) is known, use the change of variables z = [1/( y-g)] to convert the ODE to [dz/ dt]+(a+2bg)z = -b, which is linear.

Example

Let's solve the ODE dy/dx = [(y-x)/( x-4y)]. To see that it is homogeneous of order 0, note that

Let z = ^y/_x. Then y = xz, so dy/dx = x[dz/dx]+z. The ODE becomes

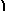
∫ 4z2-1 1-4z dz = ∫ 1 x dx ∫ -3/2 2z+1 + -1/2 2z-1 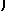dz = ∫ 1 x dx Using partial fractions - 3 4 ln|2z+1| - 1 4 ln|2z-1| = ln|x| +C1 3 ln|2z+1| + ln|2z-1| = -4ln|x| + C2 Multiplying through by -4 and relabelling -4C1 as C2. ln| (2z+1)3(2z-1)x4 | = C2 eln| (2z+1)3(2z-1)x4 | = eC2 | (2z+1)3(2z-1)x4 | = C 2 y x +1 3   2 y x -1 x4 = C Returning to the original variables using z = y/x (2y+x)3(2y-x) = C

The general solution, (2y+x)³(2y-x) = C, is written implicitly.

Finding an Integral for an Exact Equation

An ODE  N(x,y)y ′+ M(x,y) = 0  is an exact equation if (∂N)/(∂x) = (∂M)/(∂y) in a region of the xy-plane. If we can find a function H(x,y) for which (∂H)/(∂x) = M and (∂H)/(∂y) = N, then H(x,y) is called an integral of the ODE and H(x,y) = C is the general solution of the original ODE.

To find H(x,y), note that

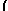
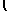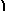
∂H ∂y = ∂ ∂y ∫ M(x,y)dx 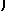+ g ′(y)

Example

The ODE ( 2yx² + 4 ) [dy/ dx] + ( 2y²x -3) = 0 is exact, since for N(x,y) = 2yx² + 4 and M(x,y) = 2y²x -3,

Integrating, g(y) = 4y, so H(x,y) = y²x²-3x+4y.

The general solution is given implicitly by

• Separable ODES: dy/dt = g(t)/ h(y)

The general solution is given by integrating ∫h(y)dy = ∫g(t)dt +C

• Linear First-Order ODEs: y ′+ p(t)y = g(t)        Use an integrating factor e^∫p(t)dt

• Homogeneous of Order Zero, Benoulli Equation, Riccati Equation:

Use the appropriate change of variable to convert the original ODE into either a separable ODE or a linear ODE.

• Exact ODEs:

N(x,y)y ′+ M(x,y) = 0, where (∂N)/(∂x) = (∂M)/(∂y)

Find H(x,y) such that (∂H)/(∂x) = M and (∂H)/(∂y) = N. The general solution is given by H(x,y) = C.