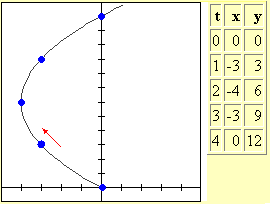
Parametric Equations Think of a curve being traced out over time, sometimes doubling back on itself or crossing itself. Such a curve cannot be described by a function y = f(x). Instead, we will describe our position along the curve at time t by x = x(t) y = y(t) . Then x and y are related to each other through their dependence on the parameter t. Example Suppose we trace out a curve according to x = t2- 4t y = 3t . where t ≥ 0. Notice how x and y vary with t. The arrow indicates the direction of increasing time or orientation of the curve. The parameter does not always represent time. Example In this parametric equation the parameter α represents the polar angle of the position on a circle of radius 2 centered at (4, 3). raggio=2 – y=3 | x=4  x = 4 + 2 cos(α) y = 3 + 2 sin(α) 0° ≤ α ≤ 360°

Differentiating Parametric Equations

Let x = x(t) and y = y(t). Suppose for the moment that we are able to re-write this as y(t) = f(x(t)). Then dy/dt = [dy/dx]·[dx/dt] by the Chain Rule. Solving for dy/dx and assuming dx/dt ≠ 0,

dy dx

=

dy dt     dx dt

,

a formula that holds in general.

Example

If x = t²-3 and y = t⁸, then dx/dt = 2t and dy/dt = 8t⁷. So

dy dx	=	dy dt dx dt = 8t7 2t = 4t6.
d2y dx2	=	d dx dy dx =   d[dy /dx] dt     dx dt   = 24t5 2t = 12t4.

Notes

• It is often possible to re-write the parametric equations without the parameter. In the second example, ^x/₃ = cos(t), ^y/₃ = sin(t). Since cos²(t)+sin²(t) = 1, (^x/₃)²+(^y/₃)² = 1. Then x²+y² = 9, which is the equation of a circle as expected. When you do eliminate the parameter, always check that you have not introduced extraneous portions of the curve.

• Every curve has infinitely many parametrizations, amounting to different scales for the parameter. For example,

  x =	3cos2θ
  y =	3sin2θ

  traces out the circle from the second example twice as "quickly," completing a full revolution in π rather than 2π units of θ.

• Every equation y = f(x) may be re-written in parametric form by letting x = t, y = f(t).

---

Key Concept [index]

A curve in the xy-plane may be described by a pair of parametric equations

x =	x(t)
y =	y(t)	,

where x and y are related through their dependence on t. This is particularly useful when neither x nor y is a function of the other.

The derivative of y with respect to x (in terms of the parameter t) is given by

dy dx

=

dy/dt dx/dt