The integrand is an improper rational function. By "long division" of polynomials, we can rewrite the integrand as the sum of a polynomial and a proper rational function "remainder":

3 2 2 3 x - 2 x - 19 x - 7 | x - x - 6 ----------- 3 2 3 2 | 3 x [ <-- 3x / x ] 3 x - 3 x - 18 x | -------------------- | 2 | 2 2 x - x - 7 | 1 [ <-- x / x ] 2 | x - x - 6 | ------------- | - 1 3 2 3 x - 3 x - 18 x -1 ———————————————— = 3x + 1 + ————————— 2 2 x - x - 6 x - x - 6

So

∫

3x3-2x2-19x-7 x2-x-6

dx =

∫

3x+1+

-1 x2-x-6

dx.

This looks much easier to work with! We can integrate 3x+1 immediately, but what about -1/(x²-x-6)?

Notice that [completing the square:
    (x-1/2)² = x²-x+1/4
    x²-x-6 = (x-1/2)²-1/4-6 = (x-1/2)²-25/4
    x²-x-6 = 0  if and only if  x-1/2 = ± 5/2  if and only if  x = -2  OR  x = 3]
x²-x-6 = (x+2)(x-3)   so that

This is called the Partial Fraction Decomposition for -1/(x²-x-6).

Our goal now is to determine A and B. Multiplying both sides of the equation by (x+2)(x-3) to clear the fractions,

There are two methods for solving for A and B:

Method 1		Method 2
Collect like terms on the right:		The equation holds for all x.
-1 = (A+B)x+(-3A+2B).		Let x = -2:
Now equate coefficients of		-1 = A(-2-3)+B(-2+2)
corresponding powers of x:		-1 = -5A      → A = 1/5.
A+B = 0,    -3A+2B = -1.		Now let x = 3:
Solving this system,		-1 = A(3-3)+B(3+2)
A = 1/5, B = -1/5.		-1 = 5B   → B = -1/5.

So

Returning to the original integral,

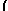
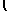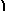
∫ 3x3-2x2-19x-7 x2-x-6  dx	=	∫ 3x+1+ [1/ 5] x+2 - [1/ 5] x-3  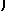dx
	=	3 2 x2+x+ 1 5 ln | | | x+2 x-3 | | | +C.

Attenzione all'uso di un programma di calcolo simbolico:
   
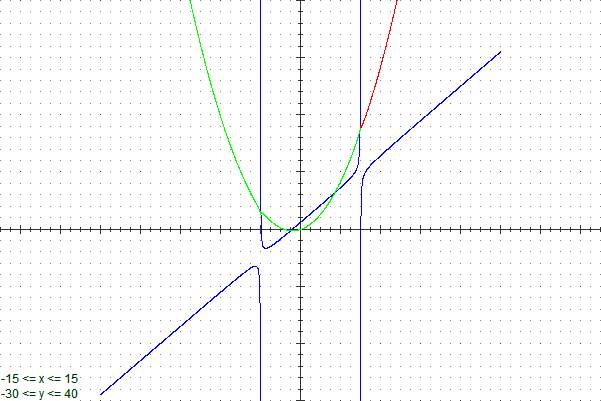
F(x) = (3*x^3-2*x^2-19*x-7) / (x^2-x-6)   (la funz. da integrare - blu)
G(x) = 1.5*x^2 + x + 1/5*log(x+2) - 1/5*log(x-3)   (la funz. integrale che può dare un programma per il calcolo simbolico - rossa)
H(x) = 1.5*x^2 + x + 1/5*log(abs((x+2)/(x-3)))   (la funz. integrale - verde e rossa)

NOTA: anche la scrittura  3/2 x² + x + 1/5 ln |(x+2)/(x−3)| + C non è, a rigore, corretta: andrebbero usate tre costanti C1, C2 e C3 diverse per ciascun intervallo in cui è definita la funzione (e la funzione H sopra riportata andrebbe, in vero, suddivisa in tre intervalli).

In the next example, we have repeated factors in the denominator, as well as an irreducible quadratic factor.

Example 2

We will evaluate

The integrand is a proper rational function, which we would like to decompose into proper rational functions of the form

[Notice that we have two factors of x in the denominator of the integrand, leading to terms of the form ^A/_x and B/(x²) in the decomposition. The factor x²+x+1 is irreducible and quadratic, so any proper rational function with x²+x+1 as denominator has the form (Cx+D)/( x²+x+1) where C or D may be 0.]

Set

Multiplying through by x²(x²+x+1),

Since x²+x+1 has no real roots, it is easiest to solve for A and B using Method 1:

Collecting like terms on the right,

Equating corresponding powers of x,

A+C = 0 A+B+D = 0 A+B = 1 B = -1

→

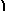
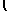
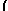
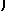A = 2 B = -1 C = -2 D = -1

→

2 x

-

1 x2

-

2x+1 x2+x+1

So

∫ x-1 x2(x2+x+1)  dx	=	∫ 2 x - 1 x2 - 2x+1 x2+x+1  dx
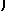	=	2ln|x|+ 1 x -ln|x2+x+1|+C
	=	1 x +ln | | | x2 x2+x+1 | | | +C.

Nota. Il procedimento visto sopra corrisponde a quello che, spesso, si fa (o si faceva) procedendo a mano, non tenendo conto dei problemi di dominio. Ad esempio l'integranda per x=0 non è definita, quindi non ha senso esprimere il risultato con un'unica costante C. Poi |x²/(x²+x+1)| è il valore assoluto di un termine che non è mai negativo, quindi |x²/(x²+x+1)| = x²/(x²+x+1).  Con del software di calcolo simbolico (come Maple) avremmo ottenuto  int((x-1)/(x^2*(x^2+x+1)), x) = 1/x+2*ln(x)-ln(x^2+x+1)  senza alcuna indicazione della costante. Sta, poi, all'utente rendersi conto del dominio della soluzione e, eventualmente, delle diverse costanti additive da aggiungere nei diversi intervalli che formano il suo dominio.

Example 3

∫ (3t²+2t+2) / (t³+t²+t) dt

(3t²+2t+2) / (t³+t²+t) = (3t²+2t+2) / (t(t²+t+1)) =  ... [procedendo come sopra]  = t / (t²+t+1) + 2 / t

∫ 2/t dt = 2 log|t| (+C)     ∫ t / (t²+t+1) dt = ?   trasformo nella somma:

t / (t²+t+1) = (2t+1) / (t²+t+1) / 2 - 1 / (t²+t+1) / 2

∫ (2t+1) / (t²+t+1) dt = log(t²+t+1) (+C)     ∫ 1 / (t²+t+1) dt = ?   completo il quadrato:

(t+1/2)² = t²+t+1/4   t²+t+1 = (t+1/2)² + 3/4   u = t+1/2   du = dt   a = √3/2
1 / (t²+t+1) = 1 / (u²+a²)
∫ 1 / (u²+a²) du = arctan(u/a)/a (+C)

∫ 1 / (t²+t+1) dt = 2 arctan((2t+1)/√3)/√3 (+C)

∫ (3t²+2t+2) / (t³+t²+t) dt = 2 log|t| + log(t²+t+1)/2 - arctan((2t+1)/√3)/√3 (+ C)
dove è da intendersi che per t > 0 e per t < 0 si può prendere C diversamente
Con Maple avrei ottenuto subito lo stesso valore battendo  int((3*t^2+2*t+2)/(t^3+t^2+t), t).
( invece di ∫1/t dt = log|t| + C si dovrebbe scrivere ∫1/t dt = f(t) con
f(t) = log(t) + C1 per t>0, f(t) = log(-t) + C2 per t<0 ).

Partial Fraction Decomposition of a Rational Function

• If the rational function is improper, use "long division" of polynomials to write it as the sum of a polynomial and a proper rational function "remainder."

• Decompose the proper rational function as a sum of rational functions of the form

  A (x-α)k

  and

  Bx+C (x2+βx+γ)k

  (x2+βx+γ irreducible)

  where:

  • Each factor (x-α)^m in the denominator of the proper rational function suggests terms

    A1 (x-α)

    +

    A2 (x-α)2

    +…+

    Am (x-α)m

  • Each factor (x²+βx+γ)ⁿ suggests terms
    
    

    B1x+C1 (x2+βx+γ)

    +

    B2x+C2 (x2+βx+γ)2

    +…+

    Bnx+Cn (x2+βx+γ)n

  
  

• Determine the (unique) values of all the constants involved.

  • Use either Method 1 or Method 2, or a combination of both.

The partial fraction decomposition is often used to rewrite a complicated rational function integrand as a sum of terms, each of which is straightforward to integrate.