|
Concavity and the Second Derivative Test
You are learning that
the calculus is a valuable tool. One of
the most important applications of the differential calculus is to find
extreme function values . The calculus methods for finding the
maximum and minimum values of a function are the basic tools
of optimization theory, a very active branch of
mathematical research applied to nearly all
fields of practical endeavor. Although modern optimization theory
is considerably more advanced, its methods and fundamental ideas
clearly show their historical relationship to the calculus. In this
tutorial you will review how the second derivative of a
function is related to the shape of its graph and how that information can be
used to classify relative extreme values.
Some First Derivative Facts
If you have not already done so, you should review
the tutorial on the First Derivative.
Click
here to see a picture that summarizes the First Derivative Test.
Concavity
The Second Derivative Test provides a means of classifying
relative extreme values by using the sign of the second derivative
at the critical number. To appreciate this test, it is first
necessary to understand the concept of concavity.
The graph of a function f
is strictly concave upward at the point
(c,f(c)) [or: f is convex at c] if f′(c) exists and if for all x in some open interval
containing c, the point (x,f(x)) on the
graph of f
lies above the corresponding point on the graph of the tangent line
to f at c. This is expressed by the inequality
f(x) > f(c) + f′(c)(x-c) for all
x in some open interval containing c.
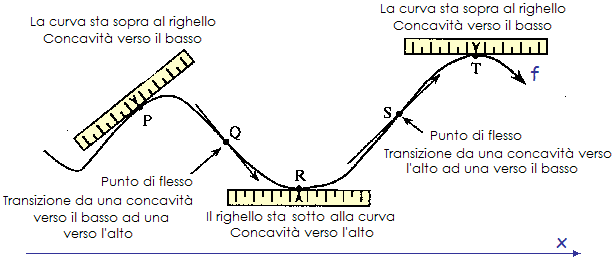
Imagine holding a ruler along the tangent line through the point
(c,f(c)): if the ruler supports the graph of f near
(c,f(c)), then the graph of the function is concave upward.
Without "strictly" the graph may be coincides with the tangent line not only at the point of contact (but in a certain interval containing c).
The graph of a function f
is strictly concave downward at the point
(c,f(c)) [or: f is concave at c] if f′(c) exists and if for all x in some open interval
containing c, the point (x,f(x)) on the
graph of f
lies below the corresponding point on the graph of the tangent line
to f at c. This is expressed by the inequality
f(x) < f(c) + f′(c)(x-c) for all
x in some open interval containing c.
In this situation the graph of f
supports the ruler .
Without "strictly" the graph may be coincides with the tangent line not only at the point of contact (but in a certain interval containing c).
This is pictured below:
Concavity and the Second Derivative
The important result that relates the concavity of the graph of
a function to its
derivatives is the following one:
Concavity Theorem:
If the function f is twice
differentiable at x = c, then the graph
of f is strictly concave upward at (c,f(c)) if f″(c) > 0 and
strictly concave downward if f″(c) < 0.
La prova è analoga a quella del First Derivative Test, usando il polinomio di
Taylor col resto nella forma di Lagrange
invece che il teorema del valor medio (ossia il polinomio di Taylor, con resto di Lagrange, di ordine 1).
Example
Suppose f(x) = x3 -3x2 + x - 2. Let's determine where the
graph of f is concave up and where it is concave down. Since f is
twice-differentiable for all x, we use the result given above and first
determine that f″(x) = 6(x -1). Thus, f″(x) > 0 if x > 1 and
f″(x) < 0
if x < 1. By the Concavity Theorem, the graph of f is concave up for x > 1 and concave down for x < 1. (→ grafico).
Inflection Points
Notice in the example above, that the concavity of the graph of f
changes sign at x = 1. Points on the graph of f where the
concavity changes from up-to-down or down-to-up are called inflection
points of the graph. The following result connects the concept of inflection
point to the derivatives properties of the function:
Inflection Point Theorem:
If f′(c) exists and f″(c) changes sign at
x = c , then the point (c,f(c)) is an inflection point of
the graph of f. If f″(c) exists at the inflection point,
then f″(c) = 0.
If we return to our example, where f(x) = x3 - 3x2 + x -2, the Inflection Point Theorem verifies that the graph of f has an inflection
point at x = 1, since f″(1) = 0.
The Second Derivative Test
The Second Derivative Test relates the concepts of critical points, extreme
values, and concavity to give a very useful tool for determining whether a
critical point on the graph of a function is a relative minimum or maximum.
The Second Derivative Test:
Suppose that c is a critical point
at which f′(c) = 0, that f′(x) exists in a neighborhood of c, and
that f″(c) exists. Then f has a relative maximum value
at c if f″(c) < 0
and a relative minimum value at c if f″(c) > 0.
If f″(c) = 0, the test is not informative.
Example:
Let's find and classify
the extreme values for the function
f with values f(x) = x3 -3x2 + x - 2 that was introduced above. We find
that f′(x) = 3x2 -6x + 1, and so there are two critical numbers where
f′(c) = 0:
|
c1 = 1 − 2√6/6 and c2 = 1 + 2√6/6. |
|
f″(c1) < 0
so f has a relative maximum at
x = 1 − 2√6/6. f″(c2) > 0, so f has a relative minumum at x = 1 + 2√6/6.
NOTA
Una funzione F si dice convessa (o con la concavità
verso l'alto) in un dato intervallo I se ivi è definita e il suo epigrafico, ossia la figura formata dall'insieme dei punti con ascissa in I
che stanno sopra al grafico di F, è convesso (ossia è tale che,
presi comunque due punti in esso, anche il segmento che li congiunge sta tutto
in esso). Se la funzione è derivabile due volte, questo equivale al fatto che
F"(x) ≥ 0 per ogni x in I.
F si dice concava (o con la concavità
verso il basso) in I se -F è convessa.
Key Concepts [index]
- Concavity Theorem:
If the function f is twice
differentiable at x = c, then the graph
of f is concave upward at (c,f(c)) if f″(c) > 0 and
concave downward if f″(c) < 0.
- The Second Derivative Test:
Suppose that c is a critical point
at which f′(c) = 0, that f′(x) exists in a neighborhood of c, and
that f″(c) exists. Then f has a relative maximum value
at c if f″(c) < 0
and a relative minimum value at c if f″(c) > 0.
If f″(c) = 0, the test is not informative.
|
