P_2n+1(x) = x - x³/3! + x⁵/5! ... + (-1)ⁿ x²ⁿ⁺¹/(2n+1)! è il polinomio di Taylor di sin(x) attorno a 0 di grado 2n+1 (il polinomio di ordine 2n+2 coincide con questo). Sotto sono tracciati i grafici in [0,9] delle corrispondenti funzioni polinomiali di grado 1, 3, 5, ….

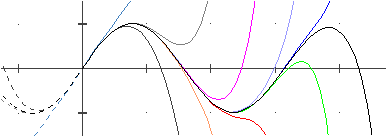
Per ogni x, lim_{m → ∞} P_m(x) = sin(x) in quanto il corrispondente resto R_m(x) = sin(x)-P_m(x), usando il teorema del resto di Lagrange, è facile vedere che (fissato x) tende a 0.
Si dice anche che la successione di funzioni P₀, P₁, P₂, P₃, … converge puntualmente alla funzione sin in R (nel senso che, preso comunque un punto x di R, P_n(x) → sin(x) per n → ∞).
Volendo parlare di convergenza di una successione di funzioni non punto per punto, ma considerando queste funzioni come oggetti globali che tendono a un'altra funzione, dobbiamo introdurre un modo per valutare la distanza tra due funzioni. Nel caso dell'esempio precedente, dobbiamo trovare un modo per esprimere una distanza d rispetto alla quale diremo che  P_n → sin  se  d(P_n, sin) → 0.
Ecco vari modi possibili di definire la distanza tra due funzioni F e G:

Scarto (assoluto) (o scarto uniforme o massimo scarto assoluto) tra F e G in [a,b]:
sup _{a ≤ x ≤ b} |F(x)-G(x)|
(l'estremo superiore del più piccolo intervallo contenente i valori assunti da |F(x)-G(x)| al variare di x in [a,b])
che coincide con  max _{a ≤ x ≤ b} |F(x)-G(x)|  se F e G sono continue (usiamo il termine "massimo scarto" anche nei casi in cui non è il massimo valore ma solo l'estremo superiore dei valori).

Scarto assoluto medio di F e G in [a,b]:
Il valor medio dello scarto assoluto: ∫_[a,b] |F(x)-G(x)| dx / (b-a)

Scarto quadratico medio di F e G in [a,b]:
La radice del valor medio del quadrato dello scarto: √( ∫_[a,b] (F(x)-G(x))² dx / (b-a) )
(che possiamo pensare anche come una specie di generalizzazione della distanza in R², R³, …, Rⁿ:  √(Δx²+Δy²),  √(Δx²+Δy²+Δz²), …,  √∑_i=1..nΔx_i²)

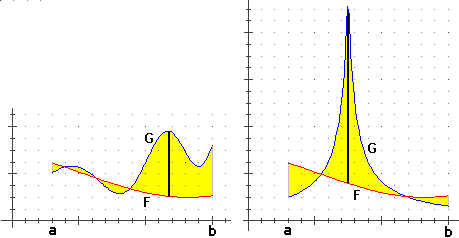
Il primo concetto (massimo scarto assoluto) è definito solo per funzioni limitate in [a,b]. Nelle figure precedenti corrisponde al segmento scuro. Rappresenta lo spessore massimo della striscia delimitata dai due grafici.
Gli altri concetti possono applicarsi anche a funzioni illimitate, se l'integrale viene inteso in senso improprio. Danno una valutazione media dello spessore; quindi (come si dimostra facilmente) hanno valore minore o uguale al massimo scarto assoluto. Lo scarto assoluto medio, in particolare, è l'altezza di un rettangolo di stessa larghezza (base) e stessa area della striscia.

A seconda di quale distanza d si usi, data una successione di funzioni f_n e una funzione F definite su [a,b], se d(f_n, F) → 0 per n → ∞, si dice che f_n converge a F uniformemente,  in media  o  in media quadratica.

La convegrenza uniforme, su cui ci soffermiamo, equivale a dire che, per ogni ε positivo esiste N tale che, comunque si prenda x in [a,b], |f_n(x) - F(x)| < ε per ogni n ≥ N.
Ossia si trova n tale che, da lì in poi, f_n(x) approssimi F(x) a meno di ε non per un x particolare, ma per tutti gli x dell'intervallo. La determinazione di N non è "punto per punto", ma vale "uniformemente", per tutti i punti.

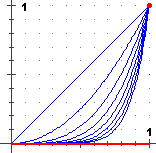
Per quanto osservato sopra (il massimo scarto è maggiore degli scarti medi) la convergenza uniforme è più forte delle altre. È evidentemente anche più forte di quella puntuale. Ecco un esempio:   fn(x) = xn, 0 ≤ x ≤ 1   F(x) = 0 se 0 ≤ x < 1, F(1) = 0 [nella figura a fianco sono raffigurati i casi n = 1, 2, …, 8] fn(x) → F(x) puntualmente ma non uniformemente: fissato ε non riesco a trovare n tale che da lì in poi xn disti da F(x) meno di ε; il massimo scarto si mantiene uguale ad 1.

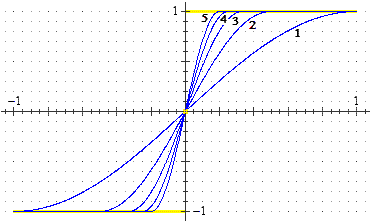
Un altro esempio:   fn(x) = sin(n x π / 2) se −1/n ≤ x ≤ 1/n   fn(x) = −1 se x ≤ −1/n   fn(x) = 1 se −1/n ≤ x   F(x) = 1 se x > 1, F(x) = −1 se x < −1, F(0) = 0 [nella figura a fianco sono raffigurati i casi n = 1, 2, …, 5] fn(x) → F(x) puntualmente ma non uniformemente. In questo caso abbiamo una successione fn di funzioni differenziabili in un intervallo, mentre F non lo è in un punto interno ad esso.

Si noti, negli ultimi esempi, che, mentre le f_n sono continue, non lo è la funzione-limite F.
Si può dimostrare facilmente che, se f_n → F uniformemente nell'intervallo I, e se le f_n sono continue in I, allora tale è anche F.
Si può pure dimostrare, nelle stesse ipotesi, che  ∫_[c,d] F = lim _{n → ∞} ∫_[c,d] f_n  in ogni sottointervallo [c,d] di I.
Dunque l'integrazione di F si può ottenerla con un passaggio al limite (con convergenza uniforme) degli integrali di f_n. La cosa non è invece detto che funzioni per la derivazione: anche nel caso di convergenza uniforme di una successione di funzioni derivabili può accadere che la successione delle derivate non converga. Comunque, se questa converge uniformemente, abbiamo che D(F) = lim _{n → ∞} D(f_n) .

Quanto detto fin qui vale per il caso particolare delle serie di funzioni, ossia quando le f_n sono del tipo:
f_n(x) = g₀(x) + g₁(x) + … + g_n(x) = Σ _{i = 0..n} g_i(x)
nel qual caso lim _{n → ∞} f_n(x) si scrive ∑ _{i = 0..∞} g_i(x).
È tale, ad es., la successione formata dai successivi polinomi di Taylor attorno ad un punto a di una stessa funzione F che ammetta derivate di ogni ordine in un intervallo I contenente a; essa viene detta serie di Taylor di punto iniziale a.
Dal teorema del resto di Lagrange segue che exp(x), sin(x) e cos(x) sono sviluppabili in serie di Taylor di punto iniziale 0 in ogni intervallo contenente 0 (ossia che la serie di Taylor corrispondente converge, e ha per somma la funzione stessa).

Le serie di Taylor sono casi particolari di serie di potenze, ossia di serie di funzioni del tipo:
∑_{k = 0 .. ∞} a_k(x – a)^k    (*)
Ne è un altro esempio, visto in Infinite Series Convergence, la serie geometrica. Si rivedano, lì, anche i criteri del rapporto (D'Alambert) e quello per le serie a segni alterni (Leibniz), oltre al concetto di "convergenza assoluta".

Supponiamo che |a_n| / |a_n+1| → R (numero reale o infinito).
Per il criterio del rapporto, dato che |a_n+1(x-a)ⁿ⁺¹| / |a_n(x-a)ⁿ| → |x-a| / R, abbiamo che la serie è assolutamente convergente per:
a - R < x < a + R
All'interno di questo intervallo di convergenza la serie converge; nei punti esterni diverge; negli estremi dell'intervallo (se R non è ∞) la cosa dipende. R viene detto raggio di convergenza.
Ciò può essere generalizzato:
• per ogni serie di potenze (*) esiste R (reale o infinito) tale che la serie converge (assolutamente) nei punti che distano da a meno di R e diverge in quelli che distano più di R (se R=0 converge solo per x=a);
• si ha inoltre che, preso comunque H < R (e positivo), in [a-H, a+H] la serie converge uniformemente (il che garantisce che la funzione somma è ivi continua, essendolo le funzioni sommate),
• e se la serie converge anche in a+R o in a-R, anche qui si ha la convergenza uniforme (e quindi la funzione somma è continua anche qui).

[il secondo fatto deriva dal fatto che il massimo scarto assoluto tra la somma S(x) e il termine n-esimo è:
max_{a-H≤x≤a+H}|S(x)-∑_0..na_k(x-a)^k| = max_{a-H≤x≤a+H}|∑_n+1..∞a_k(x-a)^k| ≤ ∑_n+1..∞|a_kH^k|
dove l'ultimo termine tende a 0 in quanto resto di una serie che converge essendo H all'interno dell'intervallo di convergenza].

Si ha inoltre che, se f(x) = ∑ _k=0..∞ a_k (x−a)^k, D(f)(x) = ∑ _k=1..∞ k a_k (x−a)^k−1 per x in (a-R, a+R).
Inoltre f(a) = a₀, f'(a) = a₁, f"(a) = 2 a₂, … e, in generale, f^(k)(a) = k! a_k.

Esempio 1.   Studiare la convergenza di:
  1 - x³/(2·2²) + x⁶/(3·2⁴) - x⁹/(4·2⁶) + x¹²/(5·2⁸) - ...   [in cui ogni addendo è ottenuto dal precedente moltiplicando per x³/(m/(m-1)·2²) (dove m è il posto dell'addendo) e cambiando segno].
Si tratta di una serie di potenze, ma non posso studiare |a_n| / |a_n+1| (a_i coefficiente del termine in xⁱ) in quanto a_n+1 è 0 per n = 0, 1, 3, 4, 6, 7, ....
Posso tuttavia applicare direttamente il criterio del rapporto:
il rapporto, in valore assoluto, tra l'addendo n-esimo e il precedente è |x|³/(n/(n-1)·2²) che per n → ∞ tende a |x|³/2².
Quindi la serie converge per |x|³/2² < 1, ossia -³√4 < x < ³√4.
Dunque il raggio di convergenza è ³√4.
Per x = -³√4 la serie diverge: 1 + 1/2 + 1/3 + 1/4 + ...
Per x = ³√4 la serie (1-1/2+1/3-1/4+...) converge per il criterio di Leibniz.
Dunque la nostra serie converge uniformemente in (-³√4, ³√4].

Esempio 2.   Dallo sviluppo di 1/(1+x²) dedurre lo sviluppo di arctan(x).
La serie geometrica 1+x+x²+... converge a 1/(1-x) esattamente per |x|<1.
Deduco che 1/(1+x²) = 1 - x² + x⁴ - x⁶ + ... per -1<x<1.
Posso integrare termine a termine tra 0 e x in quanto (trattandosi di serie di potenze) la convergenza è uniforme, e ottenere:
arctan(x) = x - x³/3 + x⁵/5 - x⁷/7 + ...
Siccome la serie converge anche per x=1 (e per x=-1), anche ivi ho la convergenza uniforme.
Nota. Di qui ricavo che π/4 = arctan(1) = 1-1/3+1/5-1/7+1/9+...

Esempio 3.   Studiare la convergenza di:
  2 + 3/1! x + 4/2! x² + 5/3! x³ + ... (il coefficiente n-esimo è (n+2)/n!).
Per il criterio del rapporto la serie converge ovunque (raggio di convergenza "infinito"), in quanto a_n/a_n+1 = (n+2)(n+1)!/(n!(n+3)) → ∞.
Nota. Utilizzando lo sviluppo di exp(x) posso trovare anche la funzione somma S(x).
exp(x) = 1 + 1/1! x + 1/2! x² + 1/3! x³ + ... (raggio di convergenza ∞)
Moltiplico per x la nostra serie ottenendo:
2x + 3/1! x² + 4/2! x³ + 5/3! x⁴ + ... = x·S(x)
Integrando la serie (tra 0 e x) ottengo:
x² + 1/1! x³ + 1/2! x⁴ + 1/3! x⁵ + ... che è uguale a x²exp(x).
Dunque x·S(x) = D_x(x²exp(x)) = x(2+x)exp(x) e S(x) = (2+x)exp(x)
[posso verificare la cosa così: (2+x)exp(x) = (2+x)(1+x+x²/2!+x³/3!+...) = ...]

Esempio 4.   Sviluppare exp(x)log(1+x)
Potrei ragionare direttamente sulle proprietà dei polinomi di Taylor (e di O-grande), come fatto in alcuni esercizi proposti in un link presente in Taylor's Theorem. . Oppure posso usare il fatto che gli sviluppi di exp(x) e log(1+x) sono serie di potenze, e quindi assolutamente convergenti (vedi la NOTA 3 in Infinite Series Convergence), e fare il prodotto degli sviluppi di exp(x) e log(1+x):
exp(x)log(1+x) = (1+x+x²/2!+x³/3!+...)(x-x²/2+x³/3-...) =
x + (1-1/2)x² + (1/2!-1/2+1/3)x³ + (1/3!-1/(2·2!)+1/3-1/4)x⁴ + ... =
x + x²/2 + x³/3 + 3x⁵/40 + ...
Il raggio di convergenza della prima serie è ∞, e quello della seconda è 1 (infatti nel caso di log(1+x)  |a_n| / |a_n+1| = (n+1)/n → 1; si ha la convergenza anche per x=1, essendo ivi a segni alterni).
Quindi il risultato è valido per -1 < x < 1, quando le due serie convergono assolutamente.

Esempio 5.   Ricavare (i primi elementi de) lo sviluppo attorno a 0 di tan(x) da quelli di sin(x) e cos(x)
So che tan(x), essendo dispari, ha le derivate pari dispari. Quindi il suo sviluppo è del tipo:
a₁ x + a₃ x³ + a₅ x⁵ + ...
cos(x) = 1 - x²/2! + x⁴/4! - ...
sin(x) = x - x³/3! + x⁵/5! - ...
cos(x)tan(x) = sin(x)
(1-x²/2!+x⁴/4!-...)(a₁x+a₃x³+a₅x⁵+...) = (x-x³/3!+x⁵/5!-...)
Sviluppando ed eguagliando ricavo:
a₁ = 1, a₃ - a₁ /2! = -1/3!, a₅ - a₃ /2! + a₁ /4! = 1/5!, … da cui:
a₁ = 1, a₃ = 1/3, a₅ = 2/15, a₇ = 17/315, …

Esempio 6.   Ricavare dallo sviluppo di 1/(1-x) attorno a 0 lo sviluppo di 1/(2+x) in serie di potenze di x-1 e determinare il relativo raggio di convergeza (traccia: usare la sostituzione u = x-1).
La sostituzione suggerita serve per passare da uno sviluppo attorno a 0 a uno sviluppo attorno a 1.
Sostituendo x = u+1:
1/(2+x) = 1/(3+u) = 1/3 · 1 / (1 - (-u/3)) =
pongo t = -u/3
= 1/3 (1 + t + t² + t³ + ...) = ∑_n=0..∞(-1)ⁿ(x-1)ⁿ/3ⁿ⁺¹
|t| < 1 diventa |u/3| < 1 poi |u| < 3 poi |x-1| < 3 (ossia -2<x<4).
Il raggio di convergenza è 3.

Esempio 7.   Sviluppare in serie di potenze di x F(x) così definito:
F(x) = -1 se x=0, F(x) = log(1-x)/x altrimenti.
So che  log(1-x) = - x - x²/2 - x³/3 - ... (R=1)
Dalla serie a destra, dividendo per x, ottengo la serie di potenze
- 1 - x/2 - x²/3 - ... (R=1)
che converge a log(1-x)/x per x ≠ 0 e che per x=0 coicide con -1.
- 1 - x/2 - x²/3 - ..., che converge a una funzione continua, deve allora convergere al prolungamento per continuità in x=0 di log(1-x)/x.
F(x) → -1 = F(0) per x → 0, ossia è il prolungamento cercato. La serie trovata Fè dunque lo sviluppo in serie di potenze di x di F(x).

Esempio 8.   Approssimare ∫_[0,1] exp(-x²) dx a meno di 0.01
exp(x) = 1+x+x²/2+x³/6+x⁴/24+x⁵/120+x⁶/720+...
exp(-x²) = 1-x²+x⁴/2-x⁶/6+x⁸/24-x¹⁰/120+x¹²/720-...
Trattandosi di convergenza uniforme, l'integrale è la somma degli integrali:
∫ _[0,1] exp(-x²) dx = [x-x³/3+x⁵/10-x⁷/42+x⁹/216-x¹¹/1320+x¹³/9360-...+(-1)ⁿx²ⁿ⁺¹/((2n+1)n!)+...]_x=1
I termini alternano i segni, per cui (vedi) si alternano approssimazioni per eccesso e per difetto e il (valore assoluto del) primo termine trascurato può essere assunto come precisione, ossia come maggiorante de (valore assoluto de) l'errore.
(-1)ⁿ/((2n+1)n!) per n = 2, 3 , 4, ... (arrotondando) vale:
0.1, -0.02381, 0.004630: sono arrivato a un termine in valore assoluto minore di 0.01. Mi fermo.
∫ _[0,1] exp(-x²) dx = 1 - 1/3 + 1/10 - 1/42 + E = 0.742857... + E con 0 < E < 0.0047 < 0.01
Ovvero:
1 - 1/3 + 1/10 - 1/42 < ∫ _[0,1] exp(-x²) dx < 1 - 1/3 + 1/10 - 1/42 + 1/216
0.742857... < ∫ _[0,1] exp(-x²) dx < 0.747486...
da cui, volendo, posso ottenere la rappresentazione con meno cifre:
0.74 < ∫ _[0,1] exp(-x²) dx < 0.75
cioè: ∫ _[0,1] exp(-x²) dx = 0.74 [approssimazione per troncamento a 2 cifre significative]

Esempio 9.   Sviluppare in serie di Taylor attorno a 0 f(x) = 1/(1+x)² e g(x) = 1/(1-x)³
Dallo sviluppo di 1/(1-x) (serie geometrica) ricavo 1/(1+x) = ∑ _n=0..∞ (-1)ⁿ xⁿ che converge per x in (-1,1).
Trattandosi di serie di potenze, posso derivare termine a termine (mantenendo lo stesso raggio di convergenza):
-1/(1+x)² = ∑ _n=1..∞ (-1)ⁿ n x^n-1   da cui, cambiando segno:
1/(1+x)² = ∑ _n=1..∞ (-1)ⁿ⁺¹ n x^n-1 = 1 - 2x + 3x² - 4x³ + ...
Analogamente, derivando termine a termine lo sviluppo di 1/(1-x):
1/(1-x)² = ∑ _n=1..∞ n x^n-1   e quindi:
2/(1-x)³ = ∑ _n=2..∞ n(n-1) x^n-2   da cui:
1/(1-x)³ = ∑ _n=0..∞ (n+2)(n+1)/2 xⁿ = 1 + 3x + 6x² + 10x³ + 15x⁴ + ...

A volte si usa anche il concetto di convergenza totale:  ∑ _n=n0..∞ f_n(x)  converge totalmente in A se  ∑ _n=n0..∞ sup_x∈A |f_n(x)|  converge. Se una serie converge totalmente in A allora vi converge anche assolutamente e uniformemente. Tuttavia la serie può convergere assolutamente e uniformemente senza convergere totalmente.
Esempio d'uso: ∑ _n=1..∞ 1/(x²+n²).  |1/((x²+n²)| = 1/((x²+n²) ≤ 1/n² per ogni x reale, ∑ _n=1..∞ 1/n² converge; quindi la serie di partenza converge totalmente, e quindi uniformemente, per ogni x reale.
Altro esempio d'uso.  Una successione di funzioni che abbiano per grafico dei denti di sega come quelli raffigurati qui, "appoggiati" sull'asse x, tende ad appiattirsi su di esso; trattandosi di una convergenza totale, abbiamo anche la convergenza uniforme e quindi, siccome ogni f_n è continua, lo è anche la funzione somma F. Tuttavia si può dimostrare che F non è in alcun punto derivabile.

Nota. Le serie di potenze si possono considerare anche con variabile z e coefficienti complessi:
∑_{k = 0 .. ∞} a_k(z – a)^k
In maniera del tutto analoga al caso reale, si ha che la condizione di convergenza è del tipo |z - a| < R, che corrisponde a un cerchio di centro a e raggio R (sui punti del contorno del cerchio la convergenza va studiata di caso in caso).
In tal modo si possono definire exp(z), cos(z) e sin(z) assumendole uguali alle serie che si ottengono per z reale estendendole al caso di z complesso.
In particolare si ottiene immediatamente (formula di Eulero):
exp(i z) = cos(z) + i sin(z), ed anche:
se z = ρ(cos(θ) + i sin(θ)), z = ρ e^iθ, ed anche:
e^{i π} + 1 = 0 (che lega i numeri più importanti della matematica).

Esercizio
Verificare che exp(log(1+z)) = 1+z anche se z non è reale.
exp(u) = 1 + u + u²/2 + u³/3! + ...
log(1+x) = x - x²/2 + x³/3 - ...
Quindi, per x reale, la serie ottenuta sostituendo u con la serie di log(1+x), ossia:
1 + (x-x²/2+x³/3-...) + (x-x²/2+x³/3-...)²/2 + (x-x²/2+x³/3-...)³/3! + ...
[(Σa_i)^k è (Σa_i)(Σa_i)...(Σa_i), ossia il prodotto di k serie uguali]
dà luogo, dopo opportune semplificazioni, a 1+x.
Le proprietà di R che si usano per queste semplificazioni valgono anche in C. Quindi anche per z complessa ottengo:
exp(log(1+z)) = 1+z

Banca:
exp(x) = 1 + x + x²/2! + x³/3! + ... [ogni x]
sin(x) = x - x³/3! + x⁵/5! - ... [ogni x]
cos(x) = 1 - x²/2! + x⁴/4! - ... [ogni x]
log(1+x) = x - x²/2 + x³/3 - ... [-1 < x ≤ 1]
1/(1-x) = 1 + x + x² + x³ + ... [-1 < x < 1]
(1+x)^p = 1 + px + p(p-1)x²/2! + p(p-1)(p-2)x³/3! + ... [p numero reale, -1 < x < 1]