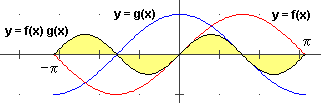
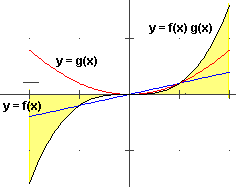
Altri spazi vettoriali

Il concetto di spazio vettoriale può essere generalizzato da quello degli usuali vettori tridimensionali ad un generico insieme S di oggetti matematici (che considereremo "vettori")
• per il quale sia definta una operazione di "somma" +
[ ossia una funzione + che ad x e y in S associ un elemento di S stesso]
• e di "moltiplicazione per uno scalare"
[ ossia una funzione che a x in S e a k numero - qualunque reale, nel qual caso di parla di spazi vettoriali su R, su cui ci soffermeremo, o qualunque complesso, nel qual caso si parla di spazi vettoriali su C - associ kx in S]
• che abbia una identità "0" per "+" rispetto a cui sia un gruppo commutativo e
• per il quale valgano la possibilità di riordinare le moltiplicazioni per gli scalari
[ h(kx) = (hk)x ],
• le proprietà distributive
[ (h+k)x = hx+kx, k(x+y) = kx+ky ]
• e la proprietà che lega lo zero di S al numero 0
[ 0x = 0 ].

Per un semplice esempio si pensi alla, ovvia, generalizzazione di quanto visto per R² e R³ a Rⁿ (n ≥ 1).
Per un altro esempio di spazio vettoriale (su R) si prenda S = {funzioni continue su [a,b]} con
(f+g)(x) = f(x)+g(x), (kf)(x) = kf(x)
prendendo come 0 di S la funzione nulla (che ad ogni x associa 0).

Sono particolarmente interessanti i casi in cui S possa essere dotato di una norma ||.|| e un prodotto scalare (o interno) · [oltre che "x·y", impiegato in particolare nel caso di Rⁿ, si usa "<x,y>"] che godano di proprietà analoghe a quelle che abbiamo visto per R³ (lo studio generale di questi casi conduce al concetto di spazio hilbertiano, su cui non ci soffermiamo).
Se S è dotato di un prodotto scalare possiamo anche dotarlo di una norma ponendo ||v|| = √(v·v).
Nel caso di Rⁿ, posto x = (x₁,..., x_n), y = (y₁,..., y_n), abbiamo:
x·y = x₁y₁ + ... + x_ny_n,  ||x|| = √(x·x) = √(x₁² + ... + x_n²).
[Nota: il prodotto vettoriale è definito solo per n=3]
Nel caso di S = {funzioni continue su [a,b]}, con una evidente analogia, possiamo prendere:
f·g = ∫_{[a, b]} f(x)g(x) dx,   ||f|| = √(f·f) = √(∫_{[a, b]} f(x)² dx)

Dalla norma possiamo ricavare la distanza d(v, u) = ||v - u||.
Nel caso dello spazio di funzioni S avremmo: d(f, g) = √( ∫_{[a, b]} (f(x)-g(x))² dx).
[si vedano le considerazioni sulla distanza di funzioni svolte a proposito delle serie di funzioni]

Col prodotto scalare possiamo generalizzare il concetto di ortogonalità:
x è ortogonale a y se x·y = 0.
Nel caso dello spazio di funzioni S abbiamo:
f ortogonale a g se  ∫_{[a, b]} f(x)g(x) dx = 0.

Esempi: f(x) = sin(x), g(x) = cos(x), [a,b] = [-π π]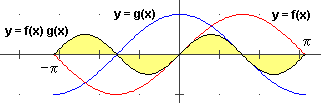
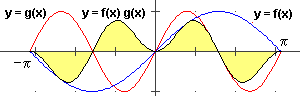
f(x) = sin(x), g(x) = sin(2x), [a,b] = [-π π]
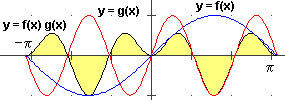
f(x) = sin(x), g(x) = sin(3x), [a,b] = [-π π]
f(x) = x, g(x) = x2, [a,b] = [-h, h]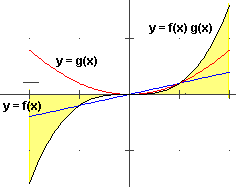

Come nel caso di R³, abbiamo che un numero finito di vettori tra loro ortogonali sono linearmenti indipendenti, e che essi possono essere normalizzati (ossia ridotti ad avere norma uguale ad 1) moltiplicandoli per il reciproco della loro norma.
Nel caso dello spazio delle funzioni continue su un intervallo [a,b] esistono infiniti vettori linearmenti indipendenti. Basti prendere, nel caso di un intervallo di ampiezza 2π, alle le funzioni x 1, x sin(nx) con n intero positivo: esse sono tutte ortogonali tra loro.  Negli altri casi basta prendere x sin(2π/(b-a)nx).
Nel caso di R³ presa comunque una base ortonormale e₁, e₂, e₃ (e_i di norma 1 e tra loro ortogonali), possiamo scomporre ogni vettore x nelle sue componenti rispetto a tale base, ossia esprimerlo come x = (x·e₁)e₁ + (x·e₂)e₂ + (x·e₃)e₃ (x·e_i è la i-esima coordinata nel sitema di riferimento associato a tale base).
La cosa vale anche per Rⁿ. Può essere generalizzata in modo opportuno anche agli spazi di dimensione infinita, ossia con infiniti vettori linearmente indipendenti x₁, x₂, x₃, …. Si ha che:
• se esiste una serie del tipo ∑ _i=1..∞ c_ix_i che converge (secondo la norma dello spazio) a x, deve essere c_i = x·x_i;
• x = ∑ _i=1..∞ (x·x_i)x_i, ossia la serie ∑ _i=1..∞ (x·x_i)x_i converge (secondo la norma dello spazio) e ha per somma x se e solo se la serie ∑ _i=1..∞ (x·x_i)² converge a ||x||²