Trigonometric Substitutions

Consider the integral

∫

dx         —— √ 9-x2

.

At first glance, we might try the substitution u = 9-x², but this will actually make the integral even more complicated!

Let's try a different approach:

The radical

_____ √ 9-x2

represents the length of the base of a right triangle with height x and hypotenuse of length 3:

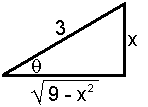For this triangle, sinθ = ^x/₃, suggesting the substitution x = 3sinθ. Then θ = arcsin(^x/₃), where we specify -π/2 ≤ θ ≤ π/2. Note that dx = 3cosθ dθ and that

_____ √ 9-x2

= 3cosθ.

With this change of variables,

∫

dx         —— √ 9-x2

=

∫

3cosθ dθ 3cosθ

=

∫

dθ = θ+C = arcsin

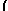
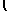x 3

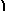
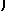+C.

Caution!

• The sketch of the triangle is very useful for determining what substitution should be made. Note, though, that the sketch only has meaning for x > 0 and θ > 0.

• It is important to be careful about how the angle θ is defined. With the restrictions on θ mentioned in the examples here, we avoid sign difficulties even when x < 0.

There are two other trigonometric substitutions useful in integrals with different forms:

Example

Let's evaluate

⌠ ⌡

dx        x2   _____ √ x2-4

.

The radical

_____ √ x2-4

suggests a triangle with hypotenuse of length x and base of length 2:

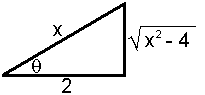For this triangle, secθ = ^x/₂, we we will try the substitution x = 2secθ. Then θ = sec^-1 (^x/₂), where we specify 0 ≤ θ < π/2 or π ≤ θ < 3π/2. Note that dx = 2secθtanθ dθ and that

_____ √ x2-4

= 2tanθ.

Then

⌠ ⌡

dx        x2   _____ √ x2-4

=

⌠ ⌡

2secθtanθ (2secθ)2(2tanθ)

dθ =

⌠ ⌡

1 4

cosθ dθ =

1 4

sinθ+C.

But we see from the sketch that

sinθ

=

_____ √ x2-4 x

.

so

⌠ ⌡

dx        x2   _____ √ x2-4

=

_____ √ x2-4 4x

+ C.

We may also use a trigonometric substitution to evaluate a definite integral, as long as care is taken in working with the limits of integration:

Example

We will evaluate

The factor (1+x²) suggests a triangle with base of length 1 and height x:

For this triangle, tanθ = x, so we will try the substitution x = tanθ. Then θ = tan^-1(x), where we specify -π/2 < θ < π/2. Here, dx = sec²θ dθ. Also,

Then

⌠ ⌡ 1 -1  dx (1+x2)2	=	⌠ ⌡ π/4 -π/4  sec2θ sec4θ  dθ The new limits of integration follow from: π/4 = arctan(1) -π/4 = arctan(-1)
	=	⌠ ⌡ π/4 -π/4  cos2θ dθ
	=	⌠ ⌡ π/4 -π/4  1 2 (1+cos2θ) dθ
	=	1 2 (θ+[1/ 2]sin2θ) | | | π/4 -π/4
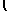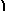
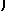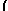
	=	1 2 π 4 + 1 2 - 1 2 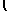- π 4 - 1 2
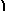
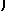	=	π 4 + 1 2 . We could also have converted the indefinite integral result back to the variable x and evaluated the result at x = 1 and x = -1.

Con Maple o altro software di calcolo simbolico questi ed altri integrali si calcolano facilmente; ad esempio per il precedente si trova come integrale indefinito  int(1/(1+x^2)^2, x) = x / (2(1+x²)) + arctan(x)/2  e come integrale definito  int(1/(1+x^2)^2, x = -1..1) = 1/2 + π/4.

Analogamente, il secondo integrale lo si ottiene immediatamente battendo  int(1/(sqrt(x^2-4)*x^2), x).  È certamente più significativo calcolare gli integrali, "strani" piuttosto che imparando a memoria i trucchi da applicare, usando le uscite di software di calcolo simbolico, e interpretandone/controllandone la significatività.

There is often more than one way to solve a particular integral. A trigonometric substitution will not always be necessary, even when the types of factors seen above appear. With practice, you will gain insight into what kind of substitution will work best for a particular integral.

Trigonometric substitutions are often useful for integrals containing factors of the form

The exact substitution used depends on the form of the integral:

(a2-x2)n	(x2+a2)n	(x2-a2)n
x = a sinθ	x = a tanθ	x = a secθ
dx = a cosθ	dx = a sec2θ	dx = a secθ tanθ
______ √ a2-x2   = a cosθ	______ √ x2+a2   = a secθ	______ √ x2-a2   = a tanθ