===== 3.1 ==================== [inizio scheda] In 2.4 abbiamo visto un possibile modo per introdurre i numeri reali, come le sequenze illimitate generabili con un opportuno diagramma di flusso: se vuoi ---> scrivi una seq. ---> scrivi -----> scrivi -----> scrivi "-" finita di cifre "." | una cifra | | | essendo le seq. fin. di <-- stai scrivendo <-- cifre definite da: un NUMERO REALE scrivi una cifra ---> vuoi continuare? -- no --> hai scritto una SEQUENZA | | si` FINITA DI CIFRE <------------------ Vediamo come affrontare le questioni (1)-(4) poste in 2.4: (1) Tra 3.7999... e 3.8000..., pensati come posizioni sulla retta o come mi- sure, non ci sono altri numeri; tale espressioni decimali indicano la stessa posizione o la stessa misura; quindi sono da intendere uguali come numeri; del resto noi sappiamo che, ad es., 0.999... e` il limite della successione 0.9, 0.99, 0.999, 0.9999, ..., ovvero di n -> 1-10^-n, ovvero della somma 9/10 + ... + 9/10^n, che vale 1. Piu` in generale, due espressioni decimali illimitate sono uguali come numeri se, tolti gli eventuali zero iniziali, esse coincidono o l'una ha periodo 9, l'altra ha periodo 0 e le cifre che precedono il periodo costituiscono due numeri naturali il primo inferiore di un'unita` rispetto al secondo: 3.7999... = 3.8000... in quanto 37+1=38. Per altre considerazioni puoi vedere gli Oggetti Matematici. (2) La limitatezza dipende dalla base: 1/3 (uno diviso tre) in base dieci non ha periodo 0 (diventa 0.333...) mentre in base 3 diventa: 0.1000... Come suggerito in 2.7, per studiare questo aspetto si puo` anche utilizzare il programma DIVISION; cambiando la riga di programma sotto evidenziata: PRINT "Per altre cifre premi 'a capo', per smettere batti f" Via: INPUT "m,n"; m, n dividendo = m: divisore = n q = dividendo \ divisore ' Calcolo il quoziente intero resto = dividendo - q * divisore ' Calcolo il resto PRINT q; "." ' Scrivo la parte intera del risultato NuovoPosto: ' Considero la potenza di 10 inferiore >> dividendo = resto * 10 << ' Esprimo il resto in questa nuova unita` q = dividendo \ divisore ' e lo divido resto = dividendo - q * divisore ' Calcolo il nuovo resto PRINT q; ' Scrivo la nuova cifra del risultato INPUT ; "", x$ IF x$ <> "" THEN PRINT : GOTO Via ELSE GOTO NuovoPosto Mettendo 3 al posto di 10 si ha il risultato espresso in base 3; ad es. per 1/2, 2/3 e 1/5 si ottengono: 0.111…, 0.2000… e 0.012101210121…. Infatti gli usuali algoritmi delle operazioni valgono qualunque sia la base di rappresentazione (il ruolo che ha 9 in base dieci viene assunto da 2 in base 3, da 1 in base 2, da 4 in base 5, ... La definizione di numero e di eguaglianza di numeri data sopra vale anche usando altri sistemi di cifre: in base 3 considereremo uguali due espressioni aventi una periodo 2 e l'altra periodo 0 e tali che ... (3) La discussione precedente (e l'uso di DIVISION) chiarisce che la periodi- cita` non dipende dalla base (considerando periodici i numeri con periodo 0). Per altre considerazioni puoi vedere gli Oggetti Matematici. (4) In questa impostazione le operazioni possono essere definite come "limi- ti": se x(n) e y(n) sono le approssimazioni di x e y (per troncamento o per arrotondamento) al posto -n, x+y, x*y, ... sono i limiti di x(n)+y(n), x(n)*y(n), ... (definendo le operazioni tra decimali limitati mediante gli usuali algoritmi). Il concetto di limite puo` essere introdotto come: miglio- rando opportunamente la precisione dei fattori posso conoscere con la preci- sione che voglio x+y, x*y, ... . Il programma INDET - vedi 2.7 - (o calcoli analoghi fatti con una calcolatrice) possono motivare (a livello di biennio) queste considerazioni; ecco ad es. il calcolo di Rad2(3)/Rad2(2) x1,x2 ? 3.1,3.2 operazione (+,-,*, / o ^) ? / y1,y2 ? 1.4,1.5 2.066666666666667 2.285714285714286 indet = .2190476 x1,x2 ? 3.16,3.17 operazione (+,-,*, / o ^) ? / y1,y2 ? 1.41,1.42 2.225352112676056 2.24822695035461 indet = 2.287484E-02 x1,x2 ? 3.162,3.163 operazione (+,-,*, / o ^) ? / y1,y2 ? 1.414,1.415 2.234628975265017 2.236916548797737 indet = 2.287574E-03 Si vede che al dividersi per 10 della indeterminazione dei fattori tende a dividersi per 10 anche la indeterminazione del risultato. Nel triennio queste considerazioni intutive possono essere meglio formalizzate. NOTA: usando il programma puo` accadere di ottenere valori visualizzati con piu` cifre di quelle che ci aspettiamo, ad es. che invece di 4.8 (come estremo di [1.4,1.5]*[3.1,3.2]) appaia 4.800000000000001. Cio` e` dovuto ai ai passaggi base 10 - base 2 - base 10 di cui si e` discusso nella scheda 2. In 2.4 si era posto il problema di come fa Derive a operare con quantita` potenzialmente illimitate di cifre. I programmi SOMMA e PRODOTTO (-> 2.7) consentono di formarsi un'idea di come cio` sia possibile. Si e` posto anche il problema di quali siano altri modi per introdurre i numeri reali. Al riguardo rinviamo alla "appendice", in 3.6.
===== 3.2 ==================== [inizio scheda] Una EQUAZIONE e` un'espressione dalla forma: Termine = Termine In alcuni libri di testo, confondendo piano sintattico (descrizione di quali espressioni del LINGUAGGIO sono da intendersi come equazioni) e piano seman- tico (che cosa sostituire a certe variabili al fine di ottenere una formula che abbia VALORE di verita` Vero?), danno definizioni diverse. ** ES.1 ******* In un libro di testo si trova: Un'EQUAZIONE e` un'eguaglianza in cui compaiono variabili e che e` vera per alcuni ma non tutti i valori dati alle variabili. Poco dopo si trova, a illustrazione di un cosiddetto "primo principio di equivalenza" (l'addizione di un monomio ai due membri fa passare a una equa- zione equivalente): 2x = 3 + x -> [addiziono -x] 2x - x = 3 + x - x -> x = 3 Provate a procedere analogamente per risolvere x+2 = 2+x e x+2 = 3+x. Poi discutete criticamente la definizione del libro. ******* END es.1 ** [commenti] L'uso di espressioni della forma Termine=Termine e, piu` in generale, l'uso del simbolo "=" assumono significati diversi in dipendenza dal CONTESTO, co- sì come si e` gia` visto per la interpretazione di una stessa espressione, che puo` dar luogo a termini diversi a seconda delle convenzioni assunte [ -> scheda 2, paragrafo 2.5 e es.6-punto 1]: - in 3+2=5 "=" viene usato come "fa", non e` percepito come "simmetrico"; nelle CT il tasto [=] sta per "esegui i calcoli impostati" - l`espressione 3x+4/2-x = 2x+2 = 2(x+1) viene intesa come una sintesi di: (1) 3x+4/2-x = 2x+2 (2) 2x+2 = 2(x+1) (3) uso della transitività per dedurre 3x+4/2-x = 2(x+1) (in questo contesto l'espressione 3x+4/2-x = 2(x+1) = 2x+2 è considerata poco sensata, anche se intendendo "=" come simbolo di eguaglianza è significativa quanto la precedente) - nelle assegnazioni dei linguaggi di programmazione (x = x+1 sta per assegna a x il valore che ha attualmente x aumentato di 1) "=" non e` usato simmetri- camente (simile e` l'uso nelle assegnazioni dei fogli di calcolo); e` simme- trico quando e` usato per costruire una Condizione in IF Condizione THEN ... - anche nelle definizioni (poni f(x) = ...), nelle indicazioni delle sostitu- zioni e del campo di variazione degli indici nelle sommatorie, ... siamo di fronte a usi non simmetrici di "=" - poi, a seconda dei contesti (descrivere proprieta`, modellizzare problemi, descrivere figure, ...) e del ruolo dato alle variabili, si sottointendono diversamente QUANTIFICATORI e VALORI di VERITA`; nelle frasi seguenti le par- ti tra parentesi quadre in genere sono omesse: - anche per i numeri complessi [e` vero che per ogni x e ogni y] x*y = y*x - e` vero che [per ogni x e ogni y] Rad2(xy) = Rad2(x)*Rad2(y) ? - [qualunque sia k, risolta rispetto a x, l'equazione] x^2 - k^2 = 1 ha 2 soluzioni - [qualunque sia r, risolta rispetto a (x,y), l'equazione] x^2 + y^2 = r^2 ha come soluzioni i punti del cerchio di centro (0,0) e raggio |r|. Un altro aspetto collegato e` l`uso del termine EQUIVALENZA (e del termine UGUAGLIANZA), il cui significato dipende dal contesto. Ad es., se pongo f(x) = x+1, g(x) = (x^3+x^2+x+1)/(x^2+1), h(x) = (x^2-1)/(x-1), ho che: - se identifico il concetto di funzione con quello di insieme di coppie "valore in ingresso, valore in uscita", f e g sono la stessa funzione - i termini f(x) e g(x) non sono uguali, bensì sono algebricamente equiva- lenti (ma non equivalenti in un programma) - f(x) e h(x) non sono algebricamente equivalenti, perche' per x=1 h(x) e` indefinito (lo sono nell'universo dei numeri diversi da 1) - ciononostante l`equazione f(x) = h(x) e` vera (cioe` e` una identita`) Spesso si sente parlare anche di equazione INDETERMINATA, attribuendo questa espressione alle equazioni con infinite soluzioni. Ma allora SIN(x)=0 (solu- zioni: nπ, n intero) e |x+1|+|x-1|=2 (soluzioni: intervallo [-1,1]) sono indeterminate? [forse questo strano uso deriva dal fatto che un tempo veniva chiamata analisi indeterminata lo studio delle infinite soluzioni intere di partico- lari equazioni algebriche a più incognite - si pensi alle terne pitagoriche, per intenderci; o dal fatto che può essere chiamato indeterminato un sistema di n equazioni algebriche lineari ad n incognite nel caso in cui una equazione sia combinazione lineare di altre, di modo che si abbia un insieme infinito di soluzioni, cioè: una retta o un piano o ... a seconda della dimensione, invece di un unico punto] Il simbolo di eguaglianza viene usato anche in senso approssimato. Per questo e per altre considerazioni su "=" puoi vedere gli Oggetti Matematici.
===== 3.3 ==================== [inizio scheda] ** ES.2 ******* Ecco alcuni esempi di errori o difficoltà che gli alunni incontrano spesso risolvendo equazioni: (1) 2x = 0 -> x = -2 (2) 2x = 0 -> x = 1/2 (3) 0x = 3 -> x = 3 (4) 3/x = 1 -> m.c.m dei denominatori ... , invece che capire subito che equivale a x=3 (5) (x-3)(x+1)=0 -> x^2-2x-3=0 -> ... , invece di capire che equivale a x-3=0 OR x+1=0 (6) 2 = x+a -> -x = -2+a -> ... , invece che -> 2-a = x -> x = 2-a (7) (x+1)(x+2)=x+1 -> -x-1+x^2+3x+2=0 -> ... , invece di usare la tra- sformaz. A*B=A -> A=0 OR B=1 (direttamente, anche senza raccogliere A) (8) 3x^2 / x = 0 -> 3x = 0 -> x=0 (non e` soluz.) usando A/A -> 1 (9) x+1+(6/2-3)*Rad2(x) = 0 -> x=-1 (non e` soluz.) usando 0*A -> 0 (10) Rad4(x^2)=2 -> Rad2(x)=2 -> x=4 (persa x=-4) con (A^B)^C -> A^(B*C) (11) Rad2(x^2)=2x+1 -> x = 2x+1 -> x=-1 (persa x=-1/3 e aggiunta x=-1) (12) x(x+2) = x -> x(x+2)/x = x/x -> x+2 = 1 -> x=-1 (persa x=0) (13) Rad2(2x+5) = x+1 -> 2x+5 = (x+1)^2 -> x^2 = 4 (aggiunta x=-2) A quali incomprensioni, confusioni concettuali, perdite di "riferimenti se- mantici" o ... sono attribuibili questi errori/difficolta`? ******* END es.2 ** [commenti] ** ES.3 ******* 1) Prova a risolvere (rispetto a x) l'eq. 11 dell'esercizio precedente grafi- camente, usando GRAFUN: - Apri GRAFUN (dal menu MACOSA). - DEFinisci la FUNZIONE x -> r(x^2) ["R" e` in Grafun e` la rad.quad.] come F; poi definisci x -> 2x+1 come G. - Vogliamo tracciare i grafici di F e G nella sottofinestra A. - Aziona il menu OPZioni e batti >> a << in modo da scegliere la finestra A. - Ora fai il GRAFico della FUNzione F definendo la SCALA che alla finestra associa il rettangolo cartesiano [-5,5]*[-5,5] (x1=-5, x2=5, ...); traccia un sistema di assi che si incrociano in (0,0); scegli come dominio [a,b] tutto [-5,5] (puoi battere come A e come B = senza ribattere -5 e 5). - Non fare zoom. Traccia il grafico di G (mantenendo invariata la scala e non cancellando la finestra). - I grafici sarebbero tracciabili facilmente anche a mano. Dai grafici puoi stimare subito il valore della soluzione e comprendere che la soluzione del punto 11 dell'es. 2 e` sbagliata 2) La "semplificazione" operata in (11) trascura il fatto che l'elevamento al quadrato presente in F(x) identifica gli output di -x e di x. In pratica con questo errore si prende come ramo sinistro (x<=0) del grafico di F il suo simmetrico rispetto all'asse x, come se F fosse la funzione x -> x. Per illustrare graficamente l'errore tracciamo il grafico di x -> x e di G: - DEFinisci come H la funzione x -> x. - Per scegliere la finestra B e darle la stessa scala data ad A dal menu OPZioni batti >> b=a <<. Poi realizza i grafici di H e G (traccia il reti- colato e gli assi). Che cosa rappresenta l'intersezione dei due grafici? 3) In Grafun possiamo RISOLVERE NUMERICAMENTE (non simbolicamente) una equa- zione del tipo f(x)=g(x) facendo degli zoom dei grafici di F e di G per tro- vare con piu` precisione l'ascissa degli eventuali punti di intersezione. Ma e` piu` comodo fare il grafico di x -> f(x)-g(x) e fare degli zoom di questo. Per trovare le intersezioni con l'asse x si puo` usare l'opzione ZERI dal menu CALC: - DEFinisci come K la funzione x -> f(x)-g(x), poi cerca lo "zero" di K in [c,d] = [-5,0]. Che cosa ottieni? [suggerimento: per leggere meglio le intersezioni con l'asse x usa intervalli aventi per ampiezza potenze di 10: 1, 0.1, 0.01, ... ] 4) Voglio trovare arrotondate ai decimi le soluzioni di (x+1)^2=(2-x)^4 AND 0 <= x <= 2, cioe` le soluzioni dell'equazione che stanno in [0,2]. - Prova a farlo graficamente tracciando, nella finestra C, il grafico di F: x -> (x+1)^2 in scala automatica in [0,2] e il grafico di G:x -> (2-x)^4 in scala invariata. - Questo problema e` alla portata di un alunno di prima superiore? - Posso individuare graficamente (approssimazioni) di tutte le soluzioni di (x+1)^2=(2-x)^4 ? Prova a farlo. Basta procedere graficamente per essere si- curo di aver trovato tutte le soluzioni o devo usare altre conoscenze? - Definisci H(x)=R(F(x)), K(x)=R(G(X)) e traccia nella finestra D in scala automatica in [-5,5] il grafico di H e, in scala invariata, quello di K. Ragionando su questi grafici e` piu` facile discutere quante sono le solu- zioni di F(x)=G(x) ? - Sai stabilire quante sono le soluzioni di x^5 + x^3 + x -7 = 0 ? ******* END es.3 ** [commenti] Nel seguito useremo GRAFUN e DERIVE. Se usi Windows, puoi tenere aperte entrambe le applicazioni (se usi Derive per Dos basta che apri un'altra ses- sione di DOS - cioe` che avvi una nuova volta il "prompt dos" senza uscire da GRAFUN - e da qui entri in DERIVE). ** ES.4 ******* Sei in DERIVE. 1) Introduci in Author/Crea l'equazione del punto 4 dell'esercizio precedente e, poi, risolvila utilizzando il comando soLve (Risolvi-Algebricamente). [ puoi anche battere direttamente, azionato Author/Crea, l'espressione SOLVE( (x+1)^2=(2-x)^4, x); vedi le osservazioni già fatte per EXPAND ] 2) Prova a risolvere in modo analogo l'equazione del punto 1 dell'es. prece- dente (e del punto 11 dell'es. 2). Se non riesci a ottenere le soluzioni pro- cedi così: - aziona Declare - Variable per dichiarare il dominio di x; restringi x a variare nei reali non-negativi; poi utilizza soLve; - aziona Declare - Variable e restringi x a variare nei reali non-positivi, poi utilizza soLve. Discuti quanto hai ottenuto. 3) Prova a risolvere (con soLve) l'equazione 8 [ 3x^2/x = 0 ] e 9 [ x+1+(6/2-3)*Rad2(x) = 0 ] dell'es.2. Che cosa ottieni? Prova a risolverla graficamente: evidenzia x+1+(6/2-3)*Rad2(x), non = 0, e aziona Plot (
), scegli di affiancare la finestra grafica e aziona
nuovamente Plot(). Che cosa ottieni?
[ Nella versione per Windows al posto del primo clic su puoi comandare
l'apertura di una finestra 2D dal menu Finestra, al posto del secondo
puoi usare il menu Traccia; per sovrapporre/affiancare le finestre
grafiche e simboliche usa il menu Finestra; per attivare una finestra e il
relativo menu si può cliccare su di essa o usare il menu Finestra;
con 
si può cancellare l'ultimo grafico.
Nella versione DOS azionato Plot viene chiesto come disporre la finestra:
scegli "Beside, column 40" ]
******* END es.4 ** [commenti]
Gli esercizi precedenti hanno messo in luce che il computer puo` sgravare
da molte attivita` meccaniche (nel tracciamento dei grafici, nel calcolo
numerico, nella manipolazione simbolica), ma che, come si e` gia` visto nelle
precedenti schede, il suo uso necessita di conoscenze matematiche e di abili-
ta` di controllo e interpretazione. La possibilita` di intrecciare tecniche
grafiche e tecniche simboliche favorisce il collegamento tra CAMPI DIVERSI
della matematica, che, nell'insegnamento tradizionale, non viene stimolato.
Si potrebbe osservare, criticamente, che l'uso di Derive, grazie alla pos-
sibilità di risolvere "algebricamente" le equazioni, rischia di impoverire
l'attività matematica. Ma, come abbiamo visto, il ragionamento è comunque
necessario per padroneggiare l'uso di Derive. Inoltre, gli alunni possono
essere forzati a usare Derive per risolvere le equazioni passo passo, espli-
citando via via i procedimenti impiegati e aggiungendo commenti integrativi
(cambiamenti del dominio, soluzioni che si perdono o aggiungono, ...).
Prima di illustrare ciò attraverso l'esercizio 6, ricordiamo le principa-
li riscritture impiegate per risolvere simbolicamente un'equazione t1 = t2:
- Trasformare t1 e/o t2
- t1 = t2 -> t2 = t1
- t1 = t2 -> F(t1) = F(t2)
Esempio: x+1 = 3 -> (x+1)-1 = 3-1 F è a 
a-1
- t1 = t2 -> F(t1, t) = F(t2, t)
Esempio: 2x+1 = 3-x -> 2x+1+x = 3-x+x F è (a,b) a+b, t e` x
** ES.5 *******
Quali condizioni/attenzioni occorre imporre/prestare applicando le regole
precedenti al fine di trasformare i problemi in problemi che abbiano le
stesse soluzioni?
******* END es.5 ** [commenti]
** ES.6 *******
Carica in Derive il file EQUAZ.mth (e` nel directory MC) e procedi come in-
dicato nel file stesso (chiudi prima la finestra 2D aperta in es.4, punto 3).
[in Derive per Windows intendi l'indicazione in #9 e quelle analoghe come:
- aziona Crea-Espressione, batti #12*3 e clicca su OK (non su Semplifica),
- poi aziona Semplifica-Base,
- poi aziona Semplifica-Sviluppa e clicca su Sviluppa
oppure come:
- aziona Crea-Espressione, batti #12*3 e clicca su Semplifica,
- poi aziona Semplifica-Sviluppa e clicca su Sviluppa ]
2*x - 1
#1 2*(3 - x) = ---------
3
#2 6*(3 - x) = 2*x - 1
#3 18 - 6*x = 2*x - 1
#4 19 - 6*x = 2*x
#5 19 = 8*x
19
#6 ---- = x
8
#7 2.375 = x
#8 "trasforma #12 cosi` da ottenere via via le stesse eq. riprodotte sopra:"
#9 "- in Author batti #12*3 poi aziona Simplify, poi aziona Expand"
#10 "- in Author batti #15+1 poi aziona Simplify"
#11 "... "
2*x - 1
#12: 2*(3 - x) = ---------
3
******* END es.6 ** [commenti]
===== 3.4 ==================== [inizio scheda] Le equazioni contenenti PARAMETRI non possono essere risolte graficamente se non per casi particolari. L'approccio grafico puo` pero` spesso essere utile per capire come al variare dei parametri cambiano le soluzioni (e per con- trollare eventuali successivi sviluppi di tipo simbolico). ** ES.7 ******* Voglio studiare le soluzioni rispetto a x dell'equazione x^3 - 2x - q = 0. 1) Traccia a mano i grafici di x -> x^3 e di x -> 2x+q per vari valori di q e stabilisci come al variare di q cambia il numero delle soluzioni. Entra in GRAFUN e verifica quanto hai fatto sopra: - seleziona la finestra A (OPZ - A) e definisci (DEF) le funzioni x -> x^3 (come F) e x -> 2x+q (come G), - definisci 0 come q - traccia (associando alla finestra grafica il rettangolo cartesiano [-2,2]*[-8,8]) i grafici di F e di G - poni q=1 e ritraccia (senza cancellare) il grafico di G - fai lo stesso per q=2. 2) In alternativa puoi fare il grafico di H: x-> F(x)-G(x). Prova a farlo nella finestra B, con la stessa scala scelta per A (OPZ - B=A), per q=0,1,2. Per questa particolare equazione entrambi i due metodi, 1) e 2), vanno bene. Il primo ha il vantaggio che e` facile da usare anche senza calcolatore: non e` difficile schizzare (o immaginare mentalmente) i grafici di x -> x^3 e di x -> 2x+q (per vari q), a differenza di quanto accade per x -> x^3-2x-q. 3) Studia come varia il numero delle soluzioni rispetto a x dell'equazione x^3 - qx - 1 = 0 tracciando nella finestra C (con la stessa scala della precedenti) il grafico di F e quello di K:x -> qx+1 per vari valori di q. 4) Se definisci F:x -> x^3 - qx - 1, assegni a q un certo valore (ad es. -2), tracci il grafico di F e definisci L:x -> x+1, se richiami il demo FASCIO.dm verranno tracciati automaticamente i grafici per q man mano incre- mentato mediante L (-> -1 -> 0 -> 1 -> 2 ->3). Fallo. In modo analogo si potevano realizzare anche i fasci considerati prima. ******* END es.7 ** [commenti] La soluzione puramente simbolica delle equazioni con parametri e` spesso dif- ficile in quanto per lo piu` non e` banale studiare i domini e valutare la iniettivita` delle funzioni applicate nelle trasformazioni: essi dipendono dai valori di piu` variabili. Ancor piu` che nel caso delle equazioni in una variabile senza parametri e` utile intrecciare ragionamenti sintattici e ra- gionamenti semantici, riferiti a piu` campi matematici, e maggiore importanza assume la verifica delle soluzioni. Maggiori sono anche "i limiti" del software per il calcolo simbolico e le esigenze di controllo da parte dell'utente. Vediamo qualche esempio. ** ES.8 ******* Utilizza DERIVE per risolvere (algebricamente) le seguenti, semplici, equazioni e discuti quanto ottieni. 1) k/x = -(k-x)/(x-k) risolta rispetto a x 2) a/c + a/(c+1) = 0 rispetto a c 3) Rad2(c) + a + b = 0 rispetto a c 4) c^2 + a + b = 0 5) Rad2(z^4) = 1 ******* END es.8 ** [commenti]
===== 3.5 ==================== [inizio scheda] Ne Gli Oggetti Matematici potete trovare qualche riflessione (tecnica e, indirettamente, didattica) sulla risoluzione delle equazioni. - Provate a delineare (a livello didattico) potenzilalita`, limiti, collega- menti con altri concetti matematici dei metodi grafici, numerici e simbolici per risolvere equazioni. - Provate a individuare ed esemplificare altre difficolta` incontrate dagli alunni nelle attivita` di manipolazione di termini ed equazioni. - Un linguaggio di programmazione come potrebbe essere usato a livello di- dattico per affrontare le tematiche discusse in questa scheda? Riflettete su questi problemi prima di affrontare la prossima scheda. All'inizio di essa verranno discusse queste questioni.
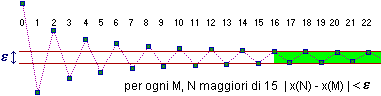
===== 3.6 ==================== [inizio scheda] APPENDICE: ancora sui numeri reali. Come sono introdotti all'universita` i numeri reali? Nei corsi di analisi matematica in genere i numeri reali vengono introdotti assiomaticamente (anche se, a volte, non si pretende di averli definiti, ma, "onestamente", si dice che se ne sono sintetizzate le proprieta`, precisando che essi esistono e si possono costruire, ma che per semplicita`, invece di dimostrarne le proprieta`, le si sono assunte come assiomi). Poi viene intro- dotto l'insieme dei numeri naturali N, ad esempio come l'intersezione di tutti i sottoinsiemi A di R (insieme dei numeri reali) t.c. 0 e` in A e se x e` in A anche x+1 e` in A. L'insieme degli interi Z viene introdotto come {x in R / x e` in N o -x e` in N}, l'insieme dei razionali Q e` introdotto come {x in R / esistono y in Z e z in N-{0} t.c. x=y/z}. La struttura (R,+,0,*,1,R+) (+ e * operazioni binarie, 0 e 1 elementi, R+ sottoinsieme, o relazione unaria) può essere descritta così (dove p.o. sta per "per ogni"): - e` un campo: (R,+,0) e (R-{0},*,1) sono gruppi commutativi, (R,*,1) e` un monoide con identita` p.o. x,y,z in R x*(y+z)=(x*y)+(x*z) - ordinato: p.o. x,y in R+ (x+y e` in R+ e x*y e` in R+) se x<>0 (x e` in R+ o -x e` in R+) 0 non sta in R+ (si pone x<y come abbreviazione di y-x sta in R+) e e` t.c. (completezza): se A e` un sottoins. di R non vuoto e limitato superiormente allora esiste S in R t.c. S=sup(A), dove: - A è limitato superiormente sta per: esiste M t.c. (-INF,M] contiene A) - S=sup(A) (usando "—>" come "implica") sta per: (-INF,S] contiene A e ( (-INF,x] contiene A —> S <= x ) S x (S è il minimo dei maggioranti di A) ------A----]-]---- Problemi (specie se non si fa la "onesta" precisazione): (A) Chi mi garantisce che R sia unico? Qui (e nel caso della presentazione assiomatica dello spazio euclideo) vogliamo definire/individuare assiomaticamente un "oggetto" matematico; e` una situazione diversa dalla definizione assiomatica dei "concetti" di gruppo, campo, ... (B) Chi mi garantisce che R esista? (l'esistenza di un modello degli assiomi, per altro, mi garantirebbe che gli assiomi non presentano contraddizioni) Ad (A) si puo` rispondere dimostrando che due strutture che soddisfino gli "assiomi di R" sono isomorfe (anche se, a essere rigorosi, anche questa "unicita` a meno di isomorfismi" e` relativa: dipende da come e` stata scelta la teoria degli insiemi in cui si opera). E a (B)? Breve panorama storico: (1) L'analisi si appoggiava alla geometria: i numeri reali erano intesi come grandezze geometriche, il significato delle operazioni era fondato su considerazioni geometriche. Somma e differenza erano ricondotte alla somma e alla differenza di segmenti. La divisione era introdotta come rapporto tra segmenti. Moltiplicazione: se a e b sono le misure di due segmenti S1 e S2 rispetto s all'unita` di misura OU, a*b e` la misura del segmento QT / costruito nel modo seguente: a*b/\T preso P su r tale che UP sia uguale a S1, presa comunque s / \ passante per O e diversa da r, preso Q su s tale che OQ sia /\Q \ uguale a S2, tracciata la parallela a UQ passante per P, T b/ \ \ e` il punto in cui questa interseca s. __/_1__\_a_\___r La giustificazione di questa scelta si appoggiava sul O U P teo. di Talete: QT / OQ = UP / OU (2) Fino agli inizi del XIX secolo ci si accontentava di questa impostazione. Questa potrebbe sembrare anche la soluzione al nostro problema (B): la geometria euclidea ci consente di costruire un modello per gli assiomi di R. Ma chi ci garantisce che esiste un modello per gli assiomi della geometria euclidea? Questo problema non turbava i matematici di allora: gli assiomi della geometria venivano intesi come una descrizione dello spazio fisico: la matematica aveva nella fisica i suoi fondamenti (analogamente non ci si preoccupava di definire matematicamente che cos'e` una funzione: veniva intesa come la descrizione di una "legge" che lega una grandezza fisica a un'altra grandezza). Solo tra la fine del XIX e l'inizio del XX secolo, messa nitidamente a fuoco la necessita` di dimostrare la non contrad- dittorieta` degli assiomi della geometria euclidea, si raggiunge questo obiettivo dimostrando che R^3 (punti: terne di numeri reali, piani: equa- zioni lineari, distanza come funzione R^3xR^3 -> R, ...) ne e` un modello. Ma a questo punto ci troviamo di fronte nuovamente al nostro problema (B). Il problema della definizione di R, invero, lo avevano gia` affrontato (intorno al 1870) Dedekind e, separatamente, Cantor. Non lo inquadravano nell'ambito delle questioni a cui abbiamo accennato sopra (esistono modelli degli assiomi di R e degli assiomi della geometria euclidea?), che sono state formulate successivamente, ma avevano l'obiettivo di dare una costruzione di R autonoma dalla geometria, a partire dai numeri naturali. Questo obiettivo viene usualmente descritto come "aritmetizzazione dell'analisi" ed era, in qualche modo, una prosecuzione del lavoro di precisazione dei concetti dell'analisi infinitesimale (che superasse il ricorso all'idea intuitiva di infinitesimo) avviato da Cauchy e da Bolzano (sviluppi di questo lavoro saranno la messa a punto del concetto di funzione e la trattazione dei numeri transfiniti, che Cantor affrontera` dando origine alla teoria degli insiemi). (3) Vediamo, dunque, la costruzione di R a partire da N, assunto come noto (e inteso come struttura (N,+,0,*,1)), seguendo (con un linguaggio piu` "moderno" ) piu` o meno l'itinerario di Dedekind. Vedremo, successivamente, in (4), l'approccio di Cantor, più semplice e intuitivo, a cui è molto simile l'approccio da noi seguito. Z viene introdotto come NxN; l'idea e` quella di introdurre i numeri relativi come differenze tra numeri naturali: le coppie (7,5), (3,1), ... hanno differenza "positiva" pari a 2, le coppie (0,4), (2,6), ... hanno differenza "negativa" pari a -4. Così come consideriamo uguali come numeri naturali le diverse espressioni 3, 03, 003,... , così ci poniamo il problema di quando due coppie (x,y) e (z,w) (x,y,z,w in N) siano da considerate uguali come numeri relativi. Per ricondursi a (N,+,0) possiamo porre: (x,y) =Z (z,w) sta per: x+w = y+z (idea: sottrazione come operazione opposta dell'addizione: x-y=z-w sse x+w=z+y) =Z e` una buona definizione di uguaglianza? Si puo` verificare facilmente che e` riflessiva, simmetrica e transitiva. Possiamo definire l'opposto di un numero relativo (m,n) così: -(m,n) sta per: (n,m). E` una "buona definizione"? cioe` è indipendente dalla coppia con cui descriviamo il numero? ossia se (p,q) =Z (m,n) ho che -(p,q) =Z -(m,n)? Anche questa verifica e` facile. Per l'addizione l'idea e` semplice: (m,n) +Z (p,q) sta per: (m+p,n+q). E` una buona definizione? Se (#): (x,y) =Z (m,n) e (z,w) =Z (p,q) devo avere: (x,y) +Z (z,w) =Z (m,n) +Z (p,q), cioe`: (x+z,y+w) =Z (m+p,n+q), cioe`: (n+q)+(x+z) = (m+p)+(y+w), che, per le proprieta` di (N,+,0,*,1), equivale a: (x+n)+(z+q) = (y+m)+(w+p), e cio` segue da (#). ** ES.9 ******* 1) Definire la moltiplicazione e la sottrazione in Z e verificare la bonta` di tali definizioni. ******* END es.9 ** [commenti] Q viene introdotto come ZxZ; (x,y) =Q (z,w) sta per (scrivendo = invece di =Z e * invece di *Z) x*w=y*z (si noti l'analogia formale con la defini- zione di =Z; ora l'idea e` quella di divisione come operazione opposta della moltiplicazione). Poi si definiscono addizione, ... NOTA. Ai nostri giorni gli "algebristi" soppiantano la parola "uguaglianza" con la parola "relazione di equivalenza" e, ad esempio, considerano come nu- meri interi la classi di equivalenza indotte da =Z, riconducendo così l'e- guaglianza tra numeri interi all'uguaglianza tra insiemi. La sostanza non cambia. R viene introdotto come insieme delle SEZIONI "](" di Q, cioe` come insieme delle coppie (A,B), con A e B sottoinsiemi di Q, tali che: (A unito B) = Q, (A intersecato B) = Vuoto, p.o. x in A e y in B x<y, B non ha primo elemento; o, equivalentemente, considerando solo la parte destra delle sezioni, come INTERVALLI "(" di Q: intervalli finali senza primo elemento, pensabili come intersezioni con Q di intervalli di R del tipo (a,INF). [ Dato un insieme ordinato (E,<), un "intervallo" di E e` un sottoinsieme I di E tale che: (x,y in I, x<z<y) —> (z in I); un intervallo "finale" e` un sottoinsieme I tale che: (x in I, x<y) —> (y in I); un sottoinsieme I e` "senza primo elemento" se: (x in I) —> (esiste y in I t.c. y<x) ] Ad es. Rad2(2) verrebbe rappresentato con la sezione (A,B) con A = {x in Q /x*x<=2}, B={x in Q / x*x>2} (A: numeri razionali che approssima- no Rad2(2) per difetto, B: numeri razionali che lo approssimano per eccesso); ovvero, piu` semplicemente, con l'intervallo {x in Q / x*x>2}. Scegliamo la seconda strada. Se x e` I e y e` J l'eguaglianza x =R y viene ricondotta all'eguaglianza tra I e J. Come x +R y si prende K = {a+b / a in I, b in J}. Come -x ("-": negazione in R) si prende K = {-p / p non e` in I, esiste q non in I t.c. p<q } [ La clausola "esiste q non in I t.c. p<q" serve per togliere l'eventuale primo elemento, in modo da avere un intervallo "(". Idea: se x e` 1.333..., cioe` I = {p in Q / 4/3 < p}, K deve essere {p / -4/3 < p}, intervallo che ha come estremo inferiore -4/3 senza contenerlo, che coincide con {p / -p < 4/3} = {-p / p < 4/3} = {-p / (non 4/3 < p) e non p = 4/3} = {-p / p non e` in I e non p = 4/3} ] Come x *R y se I e J non contengono 0 (cioe` se x e y sono "non negati- vi") si prende K = {a*b / a in I, b in K}, se 0 e` in I e non in B si prende -( (-x) *R y ), ... ** ES.10 ******* 1) Verificare che +R e` ben definita, cioe` che K e` un intervallo "(". 2) Definire <R. ******* END es.10 ** [commenti] (4) Cantor definì, invece, i numeri reali come successioni di numeri razionali soddisfacenti la condizione di Cauchy(*), definì due successioni x e y uguali "come numeri" se x(n)-y(n) -> 0 per n -> INF, definì x+y come (x+y)(n) = x(n)+y(n), ... . La condizione di Cauchy e` infatti equivalente (in R) all'esistenza del limite e, quindi, permette di individuare l'insieme di tutte le successioni convergenti senza menzionare i numeri a cui esse convergono, che, appunto, costituiscono l'insieme dei numeri reali. Potremmo anche dire che, come il passaggio da N a Z permette di rendere sempre definita la sottrazione , il passaggio a Q permette di rendere sempre definita la divisione per numeri diversi da 0, così il passaggio a R consen- te di determinare il limite di ogni successione di Cauchy. Sostanzialmente, l'approccio discusso in 3.1 si rifa alla impostazione di Cantor: l'unica differenza è che al posto di tutte le "successioni di Cauchy" si sono prese solo le successioni x(.) tali che p.o. n naturale x(n) sia l'approssimazione per troncamento alla cifra di posto -n di x(n+1); ad es. Rad2(2) è rappresentato dalla successione x(0)=1, x(1)=1.4, x(2)=1.41, x(3)=1.414, ...; 3 è rappresentato sia da x(0)=2, x(1)=2.9, x(2)=2.99, ... che da x(0)=3, x(1)=3.0, x(2)=3.00, ... (*) Ricordiamo che x(.) soddisfa la cond. di Cauchy se per ogni ε esiste K tale che per ogni M e N maggiori di K x(M) dista da x(N) meno di ε, ossia (vedi figura sotto) gli elementi della successione di posto maggiore di K stanno tutti entro una striscia ampia ε.
(5)
Ritornando al problema B posto all'inizio di 3.6, tutto sembrerebbe ricon-
dotto ai numeri naturali: definire assiomaticamente i numeri naturali e
dimostrare che questo sistema di assiomi ha un modello o dimostrare in altro
modo che non è contraddittorio (usando metodi dimostrativi più elementari
delle argomentazioni aritmetiche, altrimenti entreremmo in un circolo
vizioso). Questo era, grosso modo, l'obiettivo che aveva definito Hilbert
nei primi anni del XX sec., ma Gödel, con un famoso teorema (1931), ha
messo praticamente la parola "fine" a questi tentativi.
Non abbiamo, dunque, prove "assolute" della coerenza degli assiomi di R
e degli assiomi della geometria euclidea, ma abbiamo solo la prova che se
uno dei due sistemi di assiomi e` coerente allora e` coerente anche l'altro
(dimostrazione "relativa" di coerenza).
Ci si puo` accontentare di prendere per buono il concetto intuitivo di
successione e cercare di "costruire" la matematica sulla base di questo,
attraverso procedimenti "algoritmici", o si possono assumere come
presupposto la consistenza della teoria dei numeri naturali (basando questa
assunzione sull'esperienza secolare degli uomini nel campo dei calcoli e
delle dimostrazioni relative ai numeri naturali) e la possibilita` di
lavorare con enti infiniti.
Osserviamo, che, ormai, il dibattito sui "fondamenti della matematica" non
e` piu` volto alla ricerca di definizioni "assolute", alla ricerca di presup-
posti metafisici o "prematematici", ma e` una riflessione piu` strettamente
legata all'analisi del modo in cui lavorano i matematici, del ruolo di lin-
guaggi formali e metodi dimostrativi, dei problemi legati ai passaggi tra
teorie matematiche diverse (la traduzione della geometria nell'algebra, un
problema dei numeri reali affrontato nell'ambito dei numeri complessi, un
problema di aritmetica elementare affrontato topologicamente, la dimostra-
zione della consistenza di una teoria svolta in un'altra teoria, ...).
La natura degli "oggetti matematici" non si puo` definire cercando l'idea
platonica giusta o la realta` concreta fondante, ma, piu` laicamente, il
significato degli oggetti della matematica si chiarisce attraverso la loro
rappresentazione in linguaggi e teorie diverse, attraverso la possibilita` di
dare interpretazioni diverse dello stesso formalismo, attraverso
l'individuazione di analogie e differenze di fondo, attraverso processi di
successiva delimitazione/estensione e raffinamento dei concetti (intuitivi o
piu` o meno formalizzati) che possono anche biforcarsi, ... . Questa e` la
matematica dei "matematici", sia la matematica "pura" che la matematica
"applicata".
A queste problematiche dovrebbe, indirettamente, riferirsi anche l'insegna-
mento della matematica (nelle scelte di come impostare l'introduzione dei
concetti, la loro formalizzaione, le dimostrazioni,...). Su cio` ritorneremo.
Per approfondimenti su alcuni di questi aspetti si può vedere la sezione 4
di una raccolta di appunti su fondamenti della matematica e concetto di
algoritmo.
===== 3.7 ==================== [inizio scheda] ** Su Es.1 Da x+2=2+x si arriverebbe a 2=2 che non sarebbe un'equazione in quanto non contiene variabili; ma non sarebbe un'eq. neanche l'espressione di partenza in quanto e` vera per "tutti" i valori dati a x. Analogamente nel secondo caso si otterrebbe 2=3 che non contiene variabili e l'espres- sione iniziale non sarebbe un'equazione in quanto non c'e` alcun valore per cui l'equazione e` vera. Poi, di fronte a un'espressione del tipo F(x)=G(x) che non si sappia risolvere non potremmo a priori stabilire se e` o no un'equazione. Il pasticcio del libro e` dovuto alla confusione tra il piano sintattico (a cui appartiene il concetto di equazione) e quello semantico (a cui appartengono quelli di verita`, soluzione rispetto a ..., ...) ** Su Es.2 Si possono svolgere considerazioni per vari aspetti simili a quelle fatte a proposito della trasformazione di termini: vedi 2.6 e i commenti al precedente es.7. (1) e (2): porto il 2 dall'altra parte e in qualche posto devo metterlo. (3): porto 0 dall'altra parte e, dato che 0 non conta niente, lo cancello, o lo cancello direttamente senza portarlo di la`; ma anche: devo trovare x tale che ..., quindi la x non puo` sparire; e, poi, come si fa a scrivere 0=3? Si tratta di confusioni originate dalle interferenze tra significati con- venzionali di alcune espressioni e loro significati nel linguaggio comune, dovute a un apprendimento puramente "esperienziale" (a forza di ripetere esercizi dello stesso tipo) di procedimenti di cui non si sono compresi i collegamenti con le proprietà dei numeri e delle funzioni che stanno loro dietro. Anche (4)-(7) dimostrano la tendenza a seguire procedimenti sintattici standard senza farsi guidare e/o controllare da considerazioni semantiche. Di fronte a difficolta` come (4) e (1)-(3) possono essere di aiuto attivita` di verbalizzazione (per quale numero devo dividere 3 per ottenere 1), ma se equilibrate con altre: il rischio e` quello di consolidare le incomprensioni sul significato di "=" discusse in 3.2 e che sono dietro a (6). (7) e` lega- to anche alla tendenza a non analizzare la struttura dei termini (c'e` qual- che analogia con la difficolta` a riconoscere in: 2 una equazione "in log x"). log x - 5 log x + 6 = 0 Gli errori (8)-(11) sono tutti dovuti a trasformazioni di termini in termi- ni non algebricamente equivalenti (di dominio piu` grande, (8) e (9), o piu` piccolo, (10), o equivalenti solo in sottodomini, (11): Rad2(x^2)=|x| e` uguale a x per x>=0 (qui entra in gioco anche il concetto di funzione inver- sa). In (12) non si e` tenuto conto che applicando "/x" si restringe il dominio della equazione; vedi anche (7). In (13) si e` applicata F:x -> x^2 senza tener conto che F non e` inietti- va; posso applicare solo la funzione che si ottiene restringendo il dominio a [0,INF): l'equaz. diventa il sistema 2x+5=(x+1)^2 AND x+1 >= 0. ** Su Es.3 1,2) grafici con -5 ≤ x ≤ 5
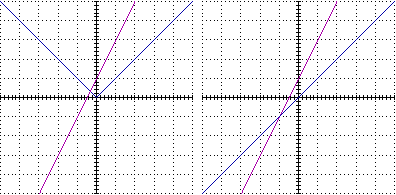F: x->|x|, G: x->2x+1 H: x->x, G: x->2x+1
3)
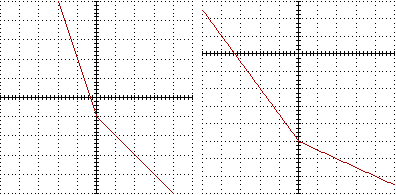x->F(x)-G(x) con -5 ≤ x ≤ 5 e con -0.5 ≤ x ≤ 0.5
Cercando numericamente lo zero si trova:
Zero di K tra C=-5 e D=0 -.3333333333333333 ~= -1/3
4) Graficamente posso studiare F(x)=G(x) solo in un insieme finito di inter-
valli limitati. Per studiare l'equazione in (-INF,INF) devo fare considera-
zioni teoriche. Ad es. F e` descrescente in (-INF,-1] e crescente in [-1,INF)
mentre G e` ... in (-INF,2] e ... in [2,INF); a destra della soluzione 4.3...
il grafico di G si mantiene sopra a quello di F poiche` G cresce piu` veloce-
mente di G; analogamente a sinistra della soluzione 0.69... si ha che ... .
Oppure si puo` considerare H:x -> G(x)-F(x) e osservare che H(x)=0 ha al piu`
4 soluzioni (essendo una eq. polinomiale di grado 4). Per x->INF e per
x->-INF H(x)->INF, interseca sicuramente 2 volte l'asse x; non puo` inter-
secarlo altre volte perche', come si vede dal grafico, ha sicuramente due
cambi di concavita` (tra 1 e 3) e di piu` non puo` averne. Oppure di puo`
tracciare anche il grafico della pendenza di H, osservare che ...
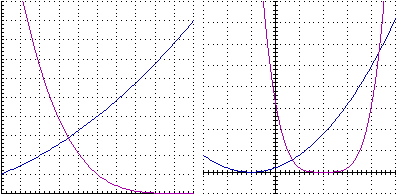F: x->(x+1)^2, G: x->(2-x)^4 con 0 ≤ x ≤ 1 e con -3 ≤ x ≤ 5
x->F(x)-G(x) con 0 ≤ x ≤ 5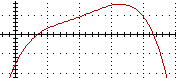 
x->R(F(x)) e x->R(G(x)) con -5 ≤ x ≤ 5 
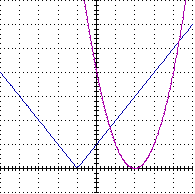- A proposito dell'ultimo punto del quesito, si puo` osservare che
x -> x^5+x^3+x-7 e` la somma di 3 funzioni crescenti, assume sia valori
positivi che negativi, quindi, essendo continua, ha un unico zero.
** Su Es.4
2) Se si dichiara x>=0 si ottiene la soluzione -1, che non appartiene al
dominio. Infatti la dichiarazione "permette" si sostituire |x| con x
ma (vedi punto 3 dei commenti a es.9 in scheda2) non impedisce poi le
successive manipolazioni che danno luogo a x=-1.
Per ottenere il risultato voluto occorre, oltre a dichiarare il dominio,
aggiungere alla espressione in un caso AND x>=0, nell'altro AND x<=0.
3) Le soluzioni x=0 e x=-1 ottenute con Derive sono dovute al fatto che
Derive prima semplifica e poi trova le soluzioni di 3x=0 e x+1=0, senza
tener conto del dominio della equazione iniziale. Anche dal grafico di
x -> x+1+(6/2-3)*Rad2(x) con Derive si otterrebbe la soluzione x=-1: il
grafico e` tracciato anche per x<1: cio` accade non perche` prima semplifi-
chi e poi faccia il grafico di x -> x+1, ma perche` (vedi i commenti all'
es.9 della scheda 2) per Derive Rad2(x) e` definito anche per ogni numero
complesso, quindi anche per x reale negativo. La soluzione x=-1 e` corretta
nell'ambiente complesso.
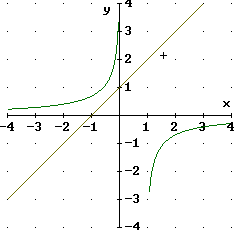
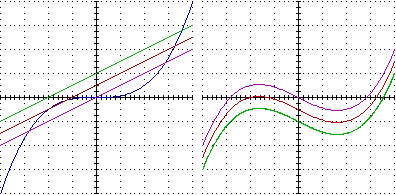
-1 
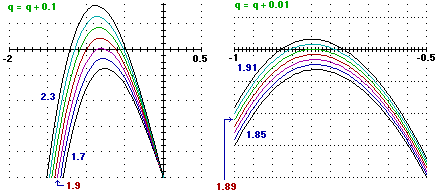Il procedimento grafico non consente di trovare i valori "esatti", ma, oltre
ad essere più comprensibile, è d'uso più generale: consente di affrontare
equazioni che non sarebbero affrontabili algebricamente.
** Su Es.8
1) Derive