===== 4.1 ==================== [inizio scheda] Confrontate le vostre riflessioni sui punti indicati alla fine della scheda 3 con le seguenti. METODI GRAFICI per risolvere le equazioni. Vantaggi: - consentono di risolvere equazioni concettualmente alla portata degli alunni senza che lo siano ancora (o senza che esistano) tecniche per risol- verle simbolicamente - facilitano il collegamento con l'eventuale problema modellizzato dall'equa- zione Limiti: - non consentono di essere sicuri di aver trovato tutte le soluzioni (si de- vono fare anche altri ragionamenti) - consentono di trovare solo soluzioni approssimate (a meno che non si ricor- ra anche ad altri ragionamenti) - funzionano solo nel caso di equazioni del tipo f(x)=0 [o, il che e` lo stesso, del tipo f(x)=g(x)] con f [e g] continue - in particolari situazioni (zeri che sono anche punti di min o di max) non si puo` essere sicuri che il grafico tocchi l'asse x - possono risentire delle approssimazioni del computer (nel calcolo e nella rappresentazione grafica) - non consentono di risolvere equazioni con parametri METODI NUMERICI (basati su approssimazioni successive) Valgono considerazioni simili a quelle fatte per i metodi grafici, con qual- che restrizione dei casi a cui sono applicabili METODI SIMBOLICI Vantaggi: - consentono di trovare soluzioni esatte - consentono di risolvere (alcune) equazioni con parametri - in molti casi sono piu` facili e comodi da applicare Limiti: - consentono di risolvere solo classi molto particolari di equazioni - richiedono (per la loro comprensione e, in vari casi, per la loro applica- zione) conoscenze matematiche piu` elevate - sono piu` difficili da controllare dei metodi grafici - il software per il calcolo simbolico spesso non e` affidabile (necessita di un controllo da parte dell'utente) Ulteriori CONSIDERAZIONI DIDATTICHE - opportunita` di integrare i vari approcci, per favorire negli alunni forme di ragionamento che sfruttino opportunamente idee, immagini mentali, riferi- menti a casi-prototipo, forme di controllo che si appoggiano a concetti e campi matematici diversi; - alcuni concetti chiave e` bene che siano anticipati rispetto a quanto acca- de nell'insegnamento tradizionale; ad es.: - affrontare da subito equazioni di vario genere (non solo algebriche), - usare precocemente i concetti di funzione (e di funzione inversa), - introdurre il concetto di continuità presto (non formalizzato mediante i limiti, ma a un primo livello appoggiandosi al computer: all'infittire della x [la domanda "altri punti?" di Grafun] si infittiscono sempre piu` anche le y [arrivando a un insieme connesso di pixel - e` la [uniforme] continuita` su intervalli, piu` semplice della continuita` puntuale) per affrontare il problema: "chi mi garantisce che ci sia una intersezione con l'asse x?"; - ... [per un'introduzione elementare ai concetti di funzione inversa e di continuità puoi vedere gli Oggetti Matematici] Esempi di impieghi didattici di un LINGUAGGIO DI PROGRAMMAZIONE - Fare semplici programmi (per calcolare tariffe, aree, ... in funzione di qualche grandezza; per calcolare medie, distribuzioni percentuali, ...; per esprimere soluzioni di equazioni in funzione di alcuni parametri, ...) e` assai importante per: - prendere confidenza con il linguaggi formali, - educarsi ad associare considerazioni sintattiche e semantiche (come posso scrivere ad un piano questo termine, che cos'e` all'origine dei risultati sbagliati che ottengo, ...), - comprendere la struttura dei termini, la composizione di funzioni, ... (ad es. si pensi a quando si spezzano assegnazioni complesse in assegnazioni piu` elementari per rendere piu` leggibile [o piu` facilmente controllabi- le] un programma o per evitare di far calcolare piu` volte sottotermini che compaiono anche in altre assegnazioni. - Alcuni algoritmi (ad es. per la ricerca degli zeri, di max/min, ... con strategie di approssimazioni successive) possono essere fatti implementare agli alunni. Ecco ad es. un programma per la ricerca degli zeri (zeri.bas in MC): - - - - - - - CLS DEFDBL A-Z PRINT "La funzione e' da definire nel SUB Segno - vedi menu View" PRINT "Scegli un intervallo [a,b] in cui cada x tale che f(x)=0" Via: INPUT ; "a=", a: INPUT " b=", b Segno a, s1: Segno b, s2 IF NOT s1 = -s2 THEN PRINT "f(a) e f(b) devono avere segni opposti": GOTO Via PRINT "batti 'f' per finire, solo 'a capo' per continuare" x1 = a: x2 = b PRINT "x1"; TAB(20); "x2" Ciclo: h = x2 - x1: x = x1 + h / 2: Segno x, s (*) IF s = s1 THEN x1 = x ELSE x2 = x PRINT x1; TAB(20); x2, : INPUT "", a$: IF a$ = "f" THEN END GOTO Ciclo SUB Segno (x, s) 'questo Sub mette in S il segno di f(x), definita in y = ... y = x + 10 - x * x (**) s = SGN(y) END SUB Ecco che cosa si può ottenere per x^5+x^3+x-7=0 se si mette y=x^5+x^3+x-7 nella riga (**) a=-10 b=10 x1 x2 0 10 0 5 0 2.5 [per un arresto automatico si potrebbe 1.25 2.5 mettere dopo la riga (*): 1.25 1.875 IF x=x1 THEN PRINT x: END 1.25 1.5625 ed eventualmente toglie la riga che 1.25 1.40625 precede GOTO Ciclo ] 1.25 1.328125 1.2890625 1.328125 1.2890625 1.30859375 1.2890625 1.298828125 1.2890625 1.2939453125 1.2890625 1.29150390625 ... 1.289546366784893 1.289546366784895 1.289546366784894 1.289546366784895 - - - - - - - ** ES.1 ******* Voglio studiare come varia il volume V della scatola ot- ______________ tenuta tagliando via 4 quadrati di lato x da una lamiera | | | | quadrata di lato 20 cm (-> figura a lato) e saldando a |___|x |___| due a due i nuovi lati lunghi x della lamiera. Posso usa- | x | re il programma P.BAS: | |L 10 INPUT ; "x"; x |___ ___| PRINT " V = "; (20 - x*2) ^ 2 * x | | | | GOTO 10 |___|______|___| oppure SCATOLA.BAS: L ' L = lato lamiera, LB = lato base scatola, A = area base scatola PRINT "Premi <Ctrl+C> per smettere" L = 20 10 INPUT ; "x"; x LB = L - x * 2 A = LB * LB V = A * x PRINT " V ="; V 'PRINT "LB ="; LB, "A ="; A GOTO 10 Supponi di voler trovare (approssimata ai mm) la dimensione dei tagli x af- finche' il volume sia massimo. Usa SCATOLA.BAS e prova a dare come input 5, 10, 15, 20. Per interpretare meglio le uscite togli l'apostrofo dalla riga 9 e riprova con gli stessi input. - Quali sono i vantaggi di SCATOLA.BAS rispetto a P.BAS? - Prova a risolvere il problema. Quali concetti usi implicitamente? ******* END es.1 ** [commenti]
===== 4.2 ==================== [inizio scheda] Proviamo a risolvere, con Derive, alcune DISEQUAZIONI. ** ES.2 ******* Utilizza DERIVE per risolvere (algebricamente, rispetto a x) le seguenti disequazioni e discuti quanto ottieni. 1) 1/x >= x 2) Rad2(-x^2-1) / Rad2(-x^2-1) > x 3) ax + 1 > 0 ******* END es.2 ** [commenti] ** ES.3 ******* Apri GRAFUN. 1) Traccia nella finestra A il grafico di F:x -> x^2/(x+1)-3.1x+2 e risolvi approssimativamente (con eventuali zoom) la disequazione F(x)>0 (per con- giungere i punti, dopo aver tracciato una adeguata quantita` di punti, batti "-1", in modo da evitare il tracciamento di tratti verticali in corrisponden- za di "salti infiniti": vedi Help, punto 32, nota 2). Quindi definisci G(x) = @S(F(x)) (in Grafun @S e` la funzione segno) e traccia nella finestra A con la stessa scala [-5,5]*[-8,8] i grafici di F e di G. Che cosa osservi? 2) Nella finestra B traccia (in [-4,4]*[-4,4] i grafici di H:x -> x^2 e di K: x-> -qx-1 per q=-1, 0, 1, 2, 3 in modo da individuare come al variare di q varia l'insieme delle soluzioni (rispetto a x) di x^2+qx+1 > 0 [volendo, puoi usare il demo FASCIO.dm: vedi punto 4 dell'Es.7 della Scheda 3] 3) Nella finestra C con la stessa scala scelta per B [ OPZ - C=B ], traccia il grafico della equazione x^2+yx+1=0, procedendo cosi` (per ulteriori infor- mazioni puoi usare l'help): GRAF - PUNTI (non congiunti) - E(x,y)=0 e battendo x^2+yx+1 (senza battere =0). Tracciato il grafico, alla domanda "registro ..." rispondi con <Esc>. Che cosa rappresenterebbero le intersezioni della retta y=q con tale grafi- co? (riferisciti al punto 2 dell'esercizio) 4) Nella finestra D con la stessa scala traccia il grafico dell'equazione @S(x^2+yx+1)-1=0. Nello scegliere l'opzione PUNTI (non congiunti) invece di 3 batti 3P (in questo modo vengono tracciati punti piu` piccoli). Che cosa rappresenta il grafico di questa equazione? (riferisciti al punto 2 dell'esercizio) NOTA. Se vuoi (se stai operando in Windows) puoi copiare le espressioni dalla scheda e importarle in Grafun in questo modo: seleziona l'espressione e copiala (Modifica-Copia o Edit-Copy), spostati in Grafun (ad es. con Alt+ Tab), trasforma la finestra Grafun in formato Windows (con Alt+Enter), dal menu della finestra attiva Incolla (clicca in alto a sinistra sulla barra della finestra, fai apparire il menu a cascata e seleziona Modifica-Incolla). Oppure puoi aprire il file F.gfu, ... o E.gfu dal directory GFU e incollare lì l'espressione; poi puoi importare il file da Grafun. ******* END es.3 ** [commenti] ** ES.4 ******* Come vanno modificate le riscritture impiegate per risolvere simbolicamente un'equazione t1 = t2 (vedi es. 5 di Scheda3) passando al caso di una disequazione t1 < t2 ? ******* END es.4 ** [commenti] Per altre riflessioni e spunti didattici sull'argomento delle disequazioni puoi vedere gli Oggetti Matematici.
===== 4.3 ==================== [inizio scheda] Con DERIVE si possono risolvere i SISTEMI LINEARI usando il comando soLve. I sistemi lineari possono essere introdotti in Author/Crea battendo le equazioni separate da virgola all'interno di una coppia di parentesi quadre: [equazione1, equazione2, ...] cioe` sotto forma di vettore (per vettori e matrici Derive usa le parentesi quadre). Come variabile incognita occorre indicare [x,y,z]. Ad esempio dopo aver creato il sistema x + 1 = y AND y·2 - x·3 = 1 (battendo in Author/Crea: [x+1=y,2y-3x=1] ): #1 [x + 1 = y, y·2 - x·3 = 1] posso impostarne la soluzione battendo in Author/Crea: solve(#1, [x,y]) in modo da ottenere: #2 [ x = 1 y = 2 ] Potevo anche scrivere direttamente SOLVE([x+1=y,2y-3x=1],[x,y]) oppure usare (in Windows) il comando Risolvi-Sistema. ** ES.5 ******* Inventa sistemi lineari di vari ordini e con quantita` finite, infinite e nulle di soluzioni, con e senza parametri, e prova a risolverli con Derive (le variabili possono essere lettere qualunque). ******* END es.5 ** I SISTEMI NON LINEARI possono essere risolti operando sostituzioni. ** ES.6 ******* Risolvi con Derive il sistema xy-1=0 AND xx+yy-3=0. L'incognita e` la coppia (x,y), ovvero le incognite sono le variabili x e y. [Scrivi le due equazioni su righe diverse. Risolvine una (quale?) rispetto a una delle variabili, poi sostituisci la soluzione nell'altra, poi ... . Per operare una sostituzione su una espressione spostati su di essa con i tasti freccia o il mouse, poi aziona Manage/Semplifica-Substitute] ******* END es.6 ** [commenti] La soluzione di un sistema in due incognite x e y e` l'insieme delle coppie (x,y) interpretabili come punti di intersezione delle figure che sono grafici delle equazioni che costituiscono il sistema. Graficamente e` possibile risolvere i sistemi in due incognite che non contengono parametri. Per tracciare le due curve delle equazioni del sistema dell'es.6 potremmo far rappresentare separatamente xy-1=0 e xx+yy-3=0, oppure possiamo far rappresentare direttamente (xy-1)(xx+yy-3)=0. ** ES.7 ******* 1) Procedi, con Derive, in quest'ultimo modo: introduci con Author/Crea (xy-1)(xx+yy-3)=0 poi aziona Plot (
) - Plot()
[vedi Scheda 3]. Che cosa ottieni?
Prova, analogamente, a rappresentare graficamente (x+2y)(x+3y)=0.
2) Per capire lo strano comportamento grafico di Derive osservato in 1) ci
serve comprendere come vengono realizzati i grafici delle equazioni in
due variabili. A tal fine traccia con GRAFUN (nella finestra A, ad es. in
[-4,4]*[-4,4]) il grafico di (xy-1)(xx+yy-3)=0 [vedi es.3,3)] e osserva
come avviene il tracciamento.
3) Nella finestra B, se vuoi con la stessa scala di A, traccia il grafico
della equazione xxyy+y^4+x^3+xyy-xx-3yy-2x+2=0.
Prova a dedurre come è scomponibile xxyy+y^4+x^3+xyy-xx-3yy-2x+2.
4) Se scrivessi al posto della equazione del punto 2 quella ottenuta scam-
biando x con y quale trasformazione geometrica subirebbe il grafico?
E nel caso della equazione del punto 3?
5) Che relazione c'e` tra il grafico di ((x-1)(y-1)-1)(xx+yy-3)=0 e quello
dell'equazione del punto 2 ? Sai stabilire quante sono le soluzioni del
sistema (x-1)(y-1)-1=0 AND xx+yy-3=0 ?
******* END es.7 ** [commenti]
NOTA. Se vuoi rivedere definizioni, risultati di calcoli, ... o altre
attività svolte con Grafun (anche in precedenti sessioni di lavoro),
puoi farlo operando su MENU.htm (il menu ipertestuale di MaCoSa, da cui
puoi accedere anche ai vari help). Puoi anche rivedere le ultime sessioni
di lavoro animate, sotto forma di "demo". Vedi l'Help di Grafun.
In Derive, svolta una serie di attività, puoi registrarla come file con
un nome a tua scelta, che puoi poi caricare in un momento successivo.
Per altre riflessioni e spunti didattici sull'argomento dei sistemi di
equazioni puoi vedere gli Oggetti Matematici. Altre riflessioni
saranno proposte nella Scheda 7.
===== 4.4 ==================== [inizio scheda] Le attivita` svolte in questa scheda ti suggeriscono ulteriori considera- zioni didattiche sull'opportunita` di modificare l'insegnamento algebrico nella scuola secondaria superiore? Quali? Pensaci prima di affrontare la prossima scheda.
===== 4.5 ==================== [inizio scheda] ** Su Es.1 Se uso P.bas senza tener conto del contesto ottengo le uscite sotto riprodotte, escluse le righe indicate con (*), che otterrei con SCATOLA.bas, dopo aver attivato (togliendo l'apice) la stampa di LB e A. x? 5 V = 500 LB = 10 A = 100 (*) x? 10 V = 0 LB = 0 A = 0 (*) x? 15 V = 1500 LB =-10 A = 100 (*) x? 20 V = 8000 LB =-20 A = 400 (*) Se non tenessi conto dei vincoli (il taglio non può superare la metà del lato) potrei supporre che all'aumentare del taglio il volume cresca. SCATOLA.bas ha una struttura che rispecchia meglio il problema, è più comprensibile e consente un controllo maggiore (sia relativamente alla correttezza del programma che alla interpretazione delle uscite). Variando gli input con incrementi minori posso osservare che passando da x=3 a x=4 il volume smette di crescere, e quindi dedurre che il max deve stare tra 2 e 4, e poi andare a considerare incrementi 10 volte piu' piccoli, ... : x? 1 V = 324 x? 2.1 V = 524.244 x? 3.21 V = 591.9766 x? 2 V = 512 \ x? 2.2 V = 535.392 x? 3.22 V = 592.0729 x? 3 V = 588 | ... ... x? 4 V = 576 / x? 3.2 V = 591.872 \ x? 3.32 V = 592.5855 \ x? 3.3 V = 592.5479 | x? 3.33 V = 592.5921 | x? 3.4 V = 592.416 / x? 3.34 V = 592.5908 / sta tra 2 e 4 sta tra 3.2 e 3.4 sta tra 3.32 e 3.34 Fermandoci a questo punto (certo sufficiente a fini pratici) potremmo dedurre che si può fare un taglio di 33.3 ± 0.1 mm. Ma chi mi assicura che non ci siano altri massimi relativi in cui V assume valore maggiore? Anche in questo caso occorre qualche riflessione teorica, che, in prima approssimazione, può appoggirsi sul grafico di V in funzione di x. Anzi, ragionando sul grafico, con qualche zoom, si può risolvere il problema:
** Su Es.2
1) Da` x <= -1 OR 0 <= x <= 1 invece di x <= -1 OR 0 < x <= 1
2) In R la disequazione ha dominio vuoto, mentre Derive semplifica e poi
risolve, dando x<1. La semplificazione sarebbe, parzialmente, giustificabile
solo in C, dove, però non ha senso risolvere disequazioni (l'ordinamento di
R non può essere esteso a C).
3) Da` la soluzione, in forma implicita, x*Segno(a)>-1/|a|. Perde il fatto
che per a=0 ogni x e` soluzione.
3-4) Le x delle intersezioni di y=q con la figura del punto 3 rappresentano
le soluzioni di x^2+qx+1 = 0; [le x de] i segmenti intersezione di y=q con
la figura del punto 4 (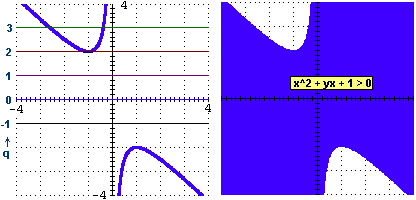
** Su Es.4
t1 < t2 -> t2 > t1 (e simili per >, <=, >=)
t1 < t2 -> F(t1) < F(t2) se F e` crescente
F(t2) < F(t1) se F e` decrescente (e simili)
** Su Es.6
Supponiamo di avere scritto:
#1 x·y - 1 = 0
#2 x·x + y·y - 3 = 0 e aver risolto #1 rispetto a x ottenendo:
#3 [x = 1/y]
A questo punto evidenzio #2, attivo Semplifica-Sostituisci, nella
finestra di dialogo che si apre seleziono x come variabile da sostituire
e nella cella a lato scrivo 1/y come termine da mettere al posto di x.
Se in #3 invece di 1/y avessi ottenuto un termine più complesso avrei
potuto evitare di batterlo: dopo aver selezionato x come variabile da
sostituire avrei potuto, senza chiudere la finestra di dialogo,
evidenziare con il mouse 1/y nella riga #3 - [x = 
(x+y^2-1)(x^2+y^2-2)=0 e "x <—> y"
(xy-1)·
(xx+yy-3)=0
((x-1)(y-1)-1)·
(xx+yy-3)=0