===== 6.1 ==================== [inizio scheda] Non ci soffermiamo esplicitamente sulle riflessioni didattiche proposte alla fine della scheda precedente, che riprendono, sia generalizzando che particolarizzando, osservazioni già svolte in schede precedenti. Potrete confrontare le vostre opinioni con quelle espresse nei seguenti materiali: 1 : "Concezioni e concetti difformi costruiti dalla scuola", riflessioni ed esempi sulle difficoltà degli alunni (all'inizio delle superiori), con particolare riferimento all'insegnamento/apprendimento numerico e algebrico 2 : Esiti di un esteso test d'ingresso all'università (datato, ma confermato da indagini parziali più recenti), con commenti 3 : Illustrazione dell'impostazione dell'insegnamento/apprendimento numerico e algebrico nel biennio scelto nel progetto MaCoSa 4 : Elenco degli argomenti affrontati negli Oggetti Matematici dal cui ordine traspare lo scheletro matematico del progetto di cui sopra (si veda, in particolare, che cosa viene prima della voce "polinomi") 5 : La voce Polinomi degli Oggetti Matematici, di cui si è già esaminato qualche paragrafo (la si scorra velocemente, per avere un'idea del filo del discorso, e ci si soffermi sull'utlimo paragrafo)
===== 6.2 ==================== [inizio scheda] Incominciamo ad esplorare aspetti didattici legati all'impiego del computer per l'elaborazione delle immagini. ** ES.1 ******* 1) Apri Paint; in genere è in "Accessori" (Start-Programmi-Accessori). Seleziona diversi strumenti (con dei clic sulla tabella di icone che li raffigura) e osserva come cambia il comportamento del mouse (se trascinato con il pulsante sinistro premuto). Vedi se ci sono dei cambiamenti se durante il trascinamento si tiene premuto il tasto-maiuscole (shift). Esamina i comandi del menu a cascata, i messaggi che compaiono se si ferma il mouse su un'icona, le informazioni che man mano appaiono nella barra di stato. Dai un'occhiata all'help. 2) Traccia un segmento e prova a traslarlo, ribaltarlo orizzontalmente e verticalmente. 3) Prova a tracciare un'ellisse non circolare e un cerchio. 4) Secondo te, a che livello scolastico si può cominciare a usare questo programma (o un programma simile)? ******* END es..1 ** [commenti] ** ES.2 ******* 1) Prova a realizzare nel modo nel modo più "veloce" possibile un parallelogramma senza lati orizzontali o verticali 2) Trova il modo di costruire un triangolo equilatero 3) Traccia un cerchio e trova un metodo generale per individuarne il centro. 4) Come fa il programma a realizzare le operazioni che noi gli comandiamo? 5) Che cosa cambia, che cosa non cambia rispetto alle costruzioni geome- triche tradizionali? ******* END es..2 ** [commenti] Per esplorare meglio la matematica incorporata nelle applicazioni grafiche, discussa nei commenti ai quesiti precedenti, vediamo come realizzare alcune immagini mediante un linguaggio di programmazione d'uso generale. ** ES.3 ******* 1) Entra in QBasic e apri il programma SPEZZATA (in MC). Prova a usare il programma. 2) Poi fermalo, posiziona il cursore sulla parola chiave WINDOW e premi F1 per avere informazioni sull'istruzione WINDOW. 3) Procedi analogamente per VIEW. 4) Prova a usare ed esamina il programma CERCHIO. 5) Aggiungi al programma Cerchio la possibilità di scegliere se tracciare un cerchio o un segmento. 6) Quali attività didattiche si possono fare con questi programmi? ******* END es..3 ** [commenti] Come sintesi degli aspetti tecnici di questa prima parte della scheda puoi esaminare i primi tre paragrafi della voce Calcolatore (5) degli Oggetti Matematici.
===== 6.3 ==================== [inizio scheda] Vogliamo studiare sperimentalmente alcune trasformazioni geometriche. Useremo, per questa attività Grafun, in quanto ha già incorporate molte trasformazioni geometriche e, soprattutto, in quanto consente di memorizzare sotto forma di file figure costituite da numerosi punti e di operare velocemente trasformazioni su tali file. Cose analoghe, ma in modo più complesso (e dispendioso in termini di "tempo" e di "spazio") sarebbero realizzabili con Derive. Diamo una idea solo di come si costruisce e memorizza una figura: - per costruire il quadrato centrato in (2,2) di lato 2 devo introdurne i vertici come vettore; posso procedere con Author/Crea battendo: [[1,1],[1,3],[3,3],[3,1],[1,1]] - per visualizzare il quadrato aziono (2 volte) Plot - se voglio che i punti non siano collegati o voglio cambiarne le dimensioni apro Punti dal menu Opzioni e intervengo sulla finestra di dialogo. Se volessi trasformare le x e le y di una figura così costruita mediante delle funzioni di x e y stesse dovrei operare una sequenza complessa di estrazioni di elementi, definizioni di nuove matrici, ... Ora apri Grafun. ** ES.4 ******* 1) Importa il file ITALIA e rappresentalo in scala automatica (come Punti Congiunti). Disegna un punto (Graf-Punti-0) con scala invariata in corrispondenza di Genova (x=8.8, y=44.4). Poi ri-rappresenta l'Italia, in [0,50]*[0,50]. 2) Utlizzando il menu CALC costruisci il file che corrisponde all'Italia ruotata di -45 gradi rispetto al punto (0,0) (Calc-TrasfFile-Rot) e rappre- senta tale file in scala invariata (senza cancellare il precedente). 3) Costruisci (usando il sottomenu MOLT: Calc-TrasfFile-Molt) il file che corrisponde alla applicazione all'Italia della funzione scala x —> x*2, y —> y*1/2 e rappresenta tale file. Che cosa conserva questa figura rispetto alla figura iniziale? 4) Definisci F(x)=C(x), G(x)=S(x), H(x)=2F(x), K(x)=G(x)/2. Traccia la curva x=H(t), y=K(t), per t in [0,360], nel quadrato [-4,4]*[-4,4] e memorizzane il grafico ad es. come dat5. [C e S sono il seno e il coseno] Poi trasforma dat5 in dat6 con una rotazione di 30 gradi attorno a (0,0) e poi dat6 in dat6 stesso con una traslazione di vettore (1/2,-1). Traccia il grafico di dat6 (Punti Congiunti). 5) Come si può definire il concetto di ellisse (senza ricorrere alla classificazione delle equazioni polinomiali in x e y di grado 2 o alla usuale caratterizzazione come "luogo geometrico")? ******* END es..4 ** [commenti] Abbiamo visto, con qualche flash, il ruolo che le trasformazioni geometriche hanno nelle applicazioni grafiche, il loro possibile impiego per costruire e per definire figure geometriche, il fatto che esse possono essere caratterizzate anche rispetto alle proprietà che conservano, ... Negli Oggetti Matematici, alla relativa voce, puoi trovare una descrizione elementare delle principali trasformazioni geometriche. Vediamo come uno studio sperimentale può aiutare a un approfondimento teorico (che poi ci può aiutare anche in un uso più efficace delle trasformazioni geometriche per scopi grafici). ** ES.5 ******* 1) Il demo PUNTEG (RCL-punteg.dm) mette in Dat9 una rappresentazione a punti del quadrato [0,1]*[0,1], che può essere impiegata per studiare trasformazioni geometriche. Avvia il demo, poi dal menu OPZ pulisci lo schermo (CLS) e seleziona la finestra A. Poi rappresenta Dat9 (come PUNTI non cong.) in [-5,5]*[-5,5]. Per una rappresentazione migliore della figura si possono far tracciare i punti in dimensione minore: torna al menu Graf, scegli Punti battendo 3P ("p" come Puntiforme) invece di 3, fai tracciare Dat9 in scala invariata cancellando la figura precedente. 2) Poi scegli la finestra B mantenendo la scala di A (Opz-B=A) e trasforma il quadrato Dat9 in un rettangolo non quadrato di stessa area ma collocato nel 4^ quadrante usando il sottomenu FUN (Calc-TrasfFile-Fun), che consente di definire la trasformazione complessiva in forma analitica. 3) Se trasformo il quadrato [0,1]*[0,1] con x'=x+y, y'=x-y quale figura ottengo? e se lo trasformo con x'=x*y, y'=x+y? Prova a rispondere con un ragionamento teorico, poi verifica la risposta mediante Grafun ed eventualmente correggi il ragionamento. 4) Esamina il demo mc\portale.dm ed elenca le trasformazioni operate per ottenere la figura finale. ******* END es..5 ** [commenti]
===== 6.4 ==================== [inizio scheda] Prima di soffermarci, nella prossima scheda, su altri aspetti delle trasfor- mazioni geometriche (e delle coniche) esploriamo i possibili collegamenti con un altro argomento: i numeri complessi. ** ES.6 ******* 1) I numeri complessi possono essere rappresentati sul piano: x + i y diventa il punto (x,y). E viceversa i punti del piano possono essere rappresentati come numeri complessi. Vai in DERIVE, introduci z*(3+4i), z^2, 1/z, poi sostituisci in tutti z con x+iy (per i usa Ctrl+I o clicca su "î" nella finestra dei simboli - usa Alt+I nella versione per Dos) e sviluppa i calcoli (anche se si tratta di calcoli che in questo caso si farebbero facilmente a mano). [per sostituire ti conviene creare l'assegnazione: z:=x+îy] Annota su un pezzo di carta le espressioni che assumono i tre termini. 2) Vai in GRAFUN, rappresenta Dat9 nella finestra A in [-5,5]*[-5,5] 3) Trasformalo (con CALC-FUN) secondo le trasformazioni z —> z+(3+4i), z —> z*(3+4i), z -z^2, z —> 1/z. Metti i trasformati in 4 file distinti, rappresenta i primi 2 in B (B=A) e gli altri in C (=A) e in D (=A). 4) Quali conclusioni puoi trarre sul significato geometrico delle operazioni tra numeri complessi. 5) Inventa altre trasformazioni e cerca di individuare se vi sono delle proprietà che tutte conservano. ******* END es..6 ** [commenti] ** ES.7 ******* Apri il programma COMPL e utilizzalo per verificare le conclusioni a cui sei giunto nel punto 4 dell'es. precedente. ******* END es..7 ** [commenti] ** ES.8 ******* Le funzioni a input e output complessi derivabili sono conformi (cioè conservano l'angolo di incidenza tra due curve) nei domini in cui la deri- vata non è nulla. Quelle del tipo z —> z*z1+z0, come si è visto, sono in particolare delle similitudini (z —> z*z1 è la composizione di una rotazione e di una omotetia avente il modulo di z1 come fattore, z —> z+z0 è una traslazione avente Re(z0) e Im(z0) come passi). Avvia GRAFUN e lancia il "demo" COMPL.DM presente in MC (comando 8 e battitura di mc\compl.dm) per vedere alcuni altri esempi. ******* END es..8 ** [commenti] Le attività svolte ti suggeriscono qualche riflessione su come introdurre e sviluppare l'argomento dei numeri complessi nella scuola superiore. Pensaci. Sul ciò ritorneremo nella prossima scheda.
===== 6.5 ==================== [inizio scheda] Abbiamo affrontato attività e questioni che fanno emergere i limiti di un insegnamento secondario della geometria basato su un approccio assiomatico: - chi mi garantisce che gli assiomi attraverso cui vorrei definire lo spazio non siano contradditori ? [questione accennata nella scheda 3] - le presentazioni assiomatiche usuali hanno come riferimento il disegno con riga e compasso, trascurano concetti spaziali molto intuitivi (come le simmetrie), sono lontane dai nuovi strumenti per disegnare (le applicazioni grafiche, che usano trasformazioni geometriche, sistemi di riferimento, ...; vedi es.2) - una separazione netta tra algebra, numeri e geometria ritarda la costruzione di immagini mentali, contesti e ed esperienze di riferimento, ... in cui queste aree si intreccino e che sono importanti per la costruzione/ comprensione profonda dei concetti, per l'ideazione di strategie risolutive, per l'esercizio di forme di controllo sui procedimenti risolutivi, ... (abbiamo visto molti esempi al riguardo), oltre a essere basata su una visione della matematica di cent'anni fa, che non tiene conto dell'attuale organizzazione della disciplina, dei nuovi settori di ricerca e di applica- zione, di dove e come interviene la matematica nella vita di tutti i giorni. Prima di approfondire queste considerazioni affrontiamo un altro esercizio: ** ES.9 ******* 1) Entra in GRAFUN, avvia il demo mc\INGANNI.dm e prova a rispondere alle domande che ti vengono proposte. Questi quesiti ti fanno venire in mente problemi che sono all'origine di alcune difficoltà degli alunni di fronte a un insegnamento "tradizionale" della geometria. 2) Come realizzare una figura usando un programma che non ha strumenti da disegno ma che accetta solo descrizioni "analitiche" (es. Derive o Grafun)? Può essere una sfida motivante per gli alunni (e che offre forme di autoverifica/autoccorrezione). Prova tu, (a) dati due cerchi disgiunti, a tracciare i segmenti non intrecciati tangenti nei loro estremi ai cerchi; (b) a tracciare una stella con i vertici in un pentagono; (c) dati due punti a tracciarne l'asse; (d) a tracciare una spirale con spire equisitanti; e (e) dato un angolo a tracciarne la bisettrice. Puoi, poi, confrontare il tuo procedimento con quello illustrato nel demo mc\FIGURE.dm. Osserva che in questi tipi di costruzioni si devono comunque fare anche dei ragionamenti non analitici, che comportano la congettura e la dimostrazione di proprietà geometriche. ******* END es..9 ** [commenti] In una dimostrazione geometrica classica non è facile gestire il confine tra argomentazioni basate sull'intuizione spaziale, costruzioni che "si vede" che si possono fare ... e quelle che effettivamente discendono dagli assiomi (o da teoremi precedenti), tanto più che spesso si ricorre a rappresentazioni grafiche che, inevitabilmente, sono solo casi particolari delle figure generiche che si vorrebbero considerare (per dirla con una battuta famosa, non si può raffigurare un triangolo generico, né scaleno, né isoscele). Più di fondo c'è il fatto che in una presentazione assiomatica della geometria è più facile ricorre, in una dimostrazione, all'utilizzo implicito di proprietà non ancora dimostrate: si usano gli stessi termini (punto, retta, segmento, …) impiegati per descrivere il concetto intuitivo di spazio che si vuole caratterizzare assiomaticamente e, quasi con un circolo vizioso, si ricorre a questo (sotto forma di disegni) anche per guidare le dimostrazioni [diverso è il caso di sistemi di assiomi che non vogliono caratterizzare un unico "oggetto matematico", ma concetti, classi di oggetti, come nei casi degli assiomi dei gruppi o delle definizioni di distanza e probabilità; in questi ambiti è più chiaro il ruolo della dimostrazione a partire degli assiomi: si vogliono individuare delle proprietà che valgono per tutti gli oggetti che verificano gli assiomi]. È più comprensibile l'idea di matematizzare l'idea intuitiva di spazio attraverso la caratterizzazione numerica dei punti e la costruzione degli altri oggetti e delle proprietà geometriche attraverso un intreccio tra approcci analitico e sintetico. Probabilmente, sono considerazioni simili a queste che hanno indotto, nella formulazione dei vari "nuovi programmi" che si sono succeduti (PNI, Brocca, programmi degli ITI, …), all'abbandono di un approccio assiomatico all'insegnamento della geometria, anche se, a dire il vero, ciò che poi è accaduto nella realtà è che molti insegnanti o hanno abbandonato del tutto la geometria o l'hanno continuata a insegnare in modo (pseudo)assiomatico. ** ES.10 ******* Esamina il demo TEO.dm per vedere un esempio di ragionamento e di dimostrazione in cui si intrecciano aspetti sintetici e analitici. ******* END es..10 ** [commenti] Le questioni sull'insegnamento della goemetria qui brevemente discusse possono essere approfondite nei seguenti materiali: - un articolo sulla "problematica del definire e del dimostrare", e, in particolare, i punti 5.2, 5.5, 5.6 (in cui sono discussi errori e problemi didattici legati alla definizione dello spazio), 6.4, 6.6, 6.7 (in cui sono discussi errori e problemi didattici legati alla dimostrazione in geometria); - un articolo sull'insegnamento della geometria in cui vengono discusse le principali difficoltà degli alunni e viene fatta una rassegna "storica" dei diversi modi in cui è stato/può essere matematizzato il concetto di spazio. - le voci degli Oggetti Matematici che si occupano più specificamente di geometria: spazio, distanza, figure(1), trasf. geometriche, figure(2) (e direzioni e funzioni circolari, continuità, lunghezza e area) - un articolo in cui (facendo riferimento all'esempio del concetto di angolo) si illustrano i problemi del raccordo tra l'insegnamento geometrico nei diversi livelli scolastici
===== 6.6 ==================== [inizio scheda] Nelle schede 1 e 2 abbiamo visto che l'osservazione e l'interpretazione del comportamento numerico di un mezzo di calcolo forniscono motivazioni per la messa a fuoco, per contrasto, delle corrispondenti proprietà dei numeri reali che i numeri-macchina non verificano, e offrono spunti anche per attività di manipolazione algebrica. Analogamente, il modo in cui vengono realizzate figure col computer offre spunti per la messa a fuoco delle proprietà degli oggetti matematici astratti corrispondenti a tali rappresentazioni. Si pensi, ad esempio, all'idea di punto e alla sua realizzazione concreta sotto forma di pixel, all'astrazione insita nella proprietà che due rette di diversa inclinazione si incontrano in un unico punto, ... :
Per commenti su questo aspetto (e sulla figura precedente) vedi Gli Oggetti
Matematici.
Accanto ad applicazioni di tipo "paint" (come quella considerata in 6.2) vi
sono applicazioni dette di tipo "draw" (in inglese "draw" indica il disegno
in senso più tecnico, "paint" quello più pittorico), in cui le figure sono
memorizzate non come insiemi di pixel ma come oggetti matematici strutturati
(segmento come coppia di punti, ...): in soldoni, vengono opportunamente
registrate le informazioni che, implicitamente, diamo azionando il mouse e/o
la tastiera mentre costruiamo la figura (la categoria di figura, le dimen-
sioni e la posizione), mentre Paint, nel momento in cui abbiamo completato
la figura, perde queste informazioni e memorizza solo lo stato finale dello
schermo. Con Paint se seleziono una parte di finestra e la ingrandisco
vengono inspessite anche le linee contenute (ad es. i pixel che compongono
un segmento diventano rettangolini più grossi), con queste applicazioni
vengono aumentate le dimensioni delle figure, non lo spessore delle linee:
la trasformazione viene operata sull'oggetto matematico che rappresenta la
figura (per il segmento vengono cambiate le coordinate degli estremi).
Chi vuol provare a usare una applicazione di questo genere può usare il
sottoprogramma per disegni incorporato in Word o quello, più sofisticato,
di StarOffice. Per qualche altra considerazione vedi Gli Oggetti Matematici.
Le applicazioni "draw" danno la possibilità di cambiare posizione e dimen-
sione delle figure cambiando, in apposite finestre di dialogo, le informa-
zioni che le caratterizzano. Alcune danno anche la possibilità, ad es., di
raggruppare figure in un'unica figura, trasformare questa e, poi, eventual-
mente, ridisgregarla nelle figure componenti, e quella di definire snap
point e snap line: ossia punti e rette "di cattura" che attraggono, a mo'
di calamita, punti caratteristici di figure che vengano a loro avvicinati
sufficientemente; ciò consente di realizzare disegni "precisi".
Un esempio. Voglio tracciare due cerchi con tangente orizzontale comune
e tracciare il segmento che ne congiunge i centri. Tracciati due cerchi:
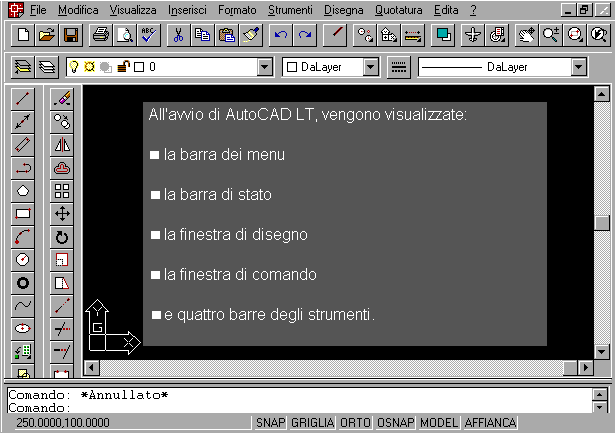Sono programmi che hanno moltissime costruzioni geometriche incorporate
(ad es. un cerchio può essere caratterizzato con raggio+centro o punto+
punto+punto o tangente+tangente+raggio o ...) e che sono dotati di strumenti
di "snap" più sofisticati; ad es. - vedi fig. sotto - si può far sì di essere
"catturati" dal centro di una figura, da un punto finale, da un punto di
intersezione, da un punto in cui si realizzi una tangenza o una
che il suo centro si sposti sul cerchio grosso. Traccio un segmento che lo
tagli (E) in modo da individuare un punto, e traslo il cerchietto indicando
mediante gli snap come punti iniziale e finale del vettore spostamento il
centro del cerchietto e il punto di intersezione ottenuto. Ottengo F.
Infine faccio una copia del nuovo cerchietto e la ruoto indicando mediante
snap come centro di rotazione il centro del cerchio grande e battendo nella
finestra comandi l'ampiezza 180 (gradi).
Queste applicazioni offrono una marea di spunti - operativi e teorici -
per l'educazione geometrica (anche tridimensionale): perché non lavorarci con
gli alunni, e/o riflettere sul loro impiego, anche nelle ore di matematica,
costruendo motivazioni reciproche per la matematica e le altre discipline,
favorendo la rottura dei compartimenti stagni tra le discipline che spesso
si crea/viene creata nella testa degli alunni, dando luogo a evidenti
sinergie, … piuttosto che usare software modellato su un settore della
"geometria scolastica", come Cabrie?
e 
consentono di far sì che la parte di piano sele-
zionata si sovrapponga a quella su cui verrà trascinata in modo opaco (ossia
coprendola anche con il proprio colore di sfondo) o in modo trasparente.
L'help fornisce indicazioni dettagliate su ciò che si può fare:
Le tecniche impiegate per la costruzione delle varie figure (tecniche che
sono diverse da quelle "scolastiche" usuali), la possibilità di fare
facilmente molti tentativi, di annullare le operazioni, ... consentono una
acquisizione operativa della padronanza dell'applicazione e, attraverso l'
interazione con la lettura dell'help (se l'insegnante spinge a un suo uso),
anche lo sviluppo di terminologie e di concetti geometrici (in modo
costruttivo, senza partire da "definizioni").
Si tratta, decisamente, di una applicazione impiegabile sin dai primissimi
livelli scolastici, e integrabile con le prime attività di educazione
geometrica e di educazione all'immagine, da affiancare, naturalmente,
all'uso di matita, carta bianca, carta quadrettata, riga, ... (e altri
sussidi: fotografie, proiezioni di immagine e ombre, ...).
** Su Es.2
1) Si può (vedi figura sotto a sinistra) (1) tracciare uno dopo l'altro una
coppia di segmenti, (2) selezionarla, (3) copiarla, incollarla, azionare
(quando la copia incollata appare ancora selezionata) un ribaltamento e,
dopo aver eventualmente selezionato l'opzione "trasparenza", traslarla col
mouse fino a far combaciare gli estremi della nuova spezzata con quelli
della vecchia. Si poteva anche tracciare (eventualmente dopo aver inspessito
il tratto) un rettangolo, selezionarlo e attivare il comando inclina, sia
verticalmente che orizzontalmente.
2) Vedi la figura sopra a destra: (1) traccia un segmento verticale,
(2) selezionalo, (3) inclina orizzontalmente di 30 °, (4) seleziona, copia
e incolla, (5) ribalta orizzontalmete e trasla, (6) traccia la "base".
3) Si può ad es, (vedi figura sotto) (1) selezionare un colore diverso e
tracciare tenendo premuto Shift 3 segmenti disposti nel modo indicato,
(2) selezionare e traslare (in trasparenza) il cerchio su tale figura,
(3) fare una copia del tutto, incollarla e ribaltarla in modo che il cerchio
si sovrapponga a sé stesso, (4) evidenziare con un colore diverso la
intersezione delle due bisettrici e cancellare le parti non contenute nel
cerchio: per far questo velocemente si possono "riempire" le parti bianche
con lo stesso colore della figura (1) e poi riempirle di bianco.
[con riga e compasso si sarebbe dovuto fare: prendere tre punti sul cerchio,
per una coppia di essi col compasso individuare due punti per cui passa
l'asse di tale coppia, fare lo stesso per un'altra coppia e prendere come
centro l'intersezione dei due assi]
4) Evidentemente il programma traduce i comandi in sottoprogrammi che
generano o trasformano le figure con tecniche analitiche: per tracciare un
segmento individua le coordinate-schermo degli estremi indicate dal mouse e
per ogni "x-schermo" compresa tra essi trova la "y-schermo" data dal numero
intero che meglio approssima la "y" che si ottiene calcolando Δy/Δx e ...;
per traslare una parte selezionata col mouse individua colore e coordinate di
ogni punto-schermo di tale parte e traccia un nuovo punto con lo stesso
colore e le coordinate schermo variate orizzontalmente e verticalmente di
quanto è stato spostato il mouse; per le ellissi usa una descrizione
parametrica; ...
5) Uso di trasformazioni geometriche, figure base costruite avendo come
riferimenti enti diversi (il cerchio e l'ellissse sono, ad es., riferiti ai
rettangoli che li circoscrivono), piano dotato di riferimenti (non è un
indistinto piano senza direzioni privilegiate), possibilità di usare le
coordinate (mouse position - posizione cursore), ... .
** Su Es.3
5) Vedi, ad es., il programma Cerchio2.bas, qui riprodotto:
5) Ad es. il cerchio x^2+y^2=1 e tutte le figure ottenibili da questo con
traslazioni, funzioni scala (cioè dilatazioni/contrazioni nelle direzioni
degli assi; ma basterebbe una sola direzione) e rotazioni sono ellissi.
In maniera analoga possono essere definite le altre coniche.
Confronta l'es.2-punto 5) e vedi gli Oggetti Matematici.
** Su Es.5
2) Ad es.: x'=x*3-4, y'=y/3-1, ottenendo il rettangolo di dimensioni 3 e 1/3
con vertice in basso a sinistra (-4,-1)
3) Si può osservare che la prima trasformazione trasforma i vertici del
quadrato i quattro punti che sono vertici di un quadrato scalato di 2 e
ruotato di -45° e che, per la sua forma algebrica, dovrebbe trasformare
rette in rette; quindi si può prevedere che assuma proprio la forma di
tale quadrato (vedi figura sotto a sinistra). Per la seconda trasformazione
si vede che i punti (a,b) e (b,a) vengono identificati (ad es. i segmenti
[0,1] e [1,0] vengono tasformati nel segmento [0,1]) per cui si ottiene
la stessa figura che si otterrebbe dal mezzo quadrato sopra a y=x. Poi:
(x,x) —> (x^2,2x) (y=x diventa la parabola x=(y/2)^2) e (x,1) —> (x,1+x)
(y=1 diventa y=1+x), per cui ci si aspetta la figura rossa sotto a sinistra.
4) Da successive trasformazioni del quadrato ottenuto con Dat9 (vedi il
demo per la loro descrizione) si ottiene la figura sopra a destra.
** Su Es.6
x'=x+3,y'=y+4; x'=3x-4y,y'=4x+3y; x'=xx-yy,y'=2xy; x'=x/(xx+yy),y'=-y/(xx+yy)
sono le trasformazioni geometriche che corrispondono alla funzioni di
variabile complessa considerate. Ecco le trasformazioni che subisce il
** Su Es.9
1) La nostra intuizione spaziale a volte ci inganna: a) segmenti uguali, per
il "disturbo" creato da altre parti della figura, ci possono sembrare
diversi; b) la dispozione delle figure ci fa supporre che alcune siano so-
vrapponibili ad altre anche se ciò non è vero (25>24); c) una figura, che
possiamo pensare come l'unione di 3 "7", ci richiama l'idea della rappresen-
tazione piana di un solido e la carichiamo di questo significato aggiuntivo
il quale, di fronte all'impossibilità di interpretare l'intera figura
tridimensionalmente, ci porta a un conflitto mentale che dà luogo anche a un
fastidio visivo; d) nel rappresentare una situazione ne illustriamo un caso
particolare e ragioniamo su quello, utilizzando senza accorgercene le ipotesi
aggiuntive fatte realizzando l'illustrazione (in questo caso trascuriamo le
situazioni in cui la proiezione della base superiore del parallelogramma non
cade su quella inferiore).
c)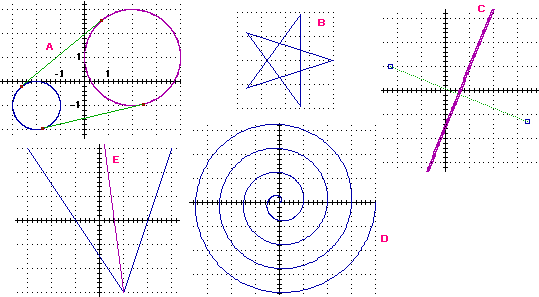
** Su Es.10
Ecco, senza animazioni, che cosa si ottiene:
teo.dm:
teo1.dm:
teo2.dm:
[inizio scheda] [schede: 1 2 3 4 5 6 7 8] [indice schede]