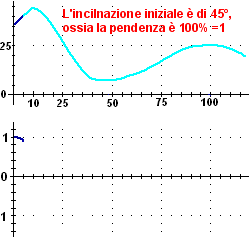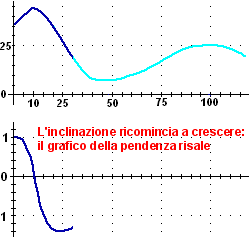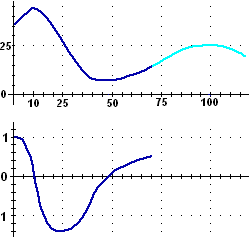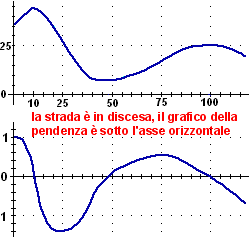
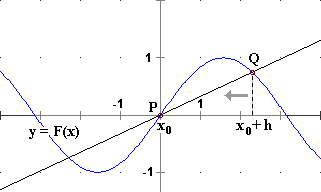
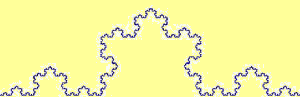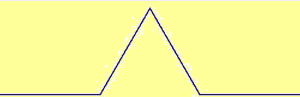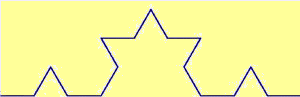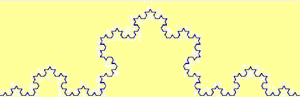
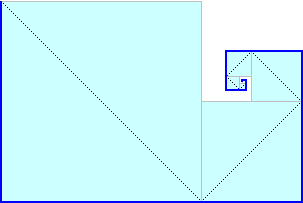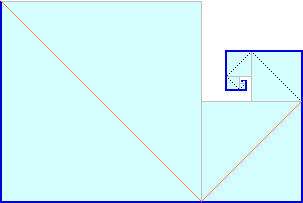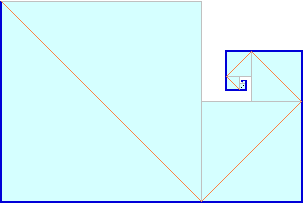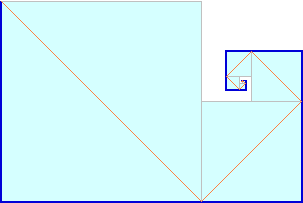
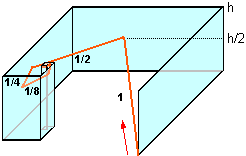
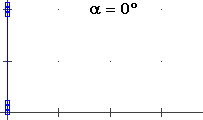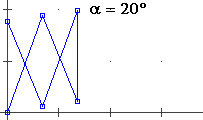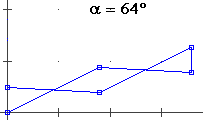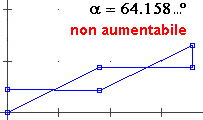Per copiare un'immagine animata cliccaci sopra col pulsante destro del mouse
To copy an animated image, click on it with the right mouse button

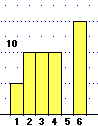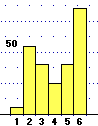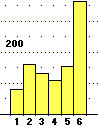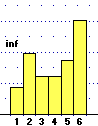
Sono di più
le femmine
o i maschi ?		 





Il termometro passa da 4° a −3°.
Di quanto è variata la temperatura?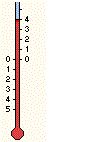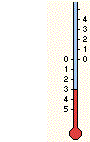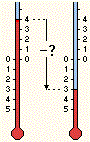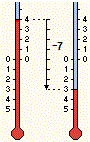		 








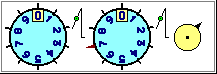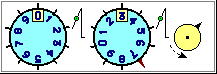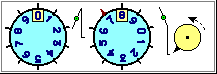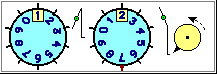
Siamo in 3. Dobbiamo mettere insieme 5 €.
Quanto dovrebbe dare ciascuno?
Uso la calcolatrice nel modo illustrato a lato.
Quanti euro e quanti centesimi deve mettere
ciascuno di noi? 		   



Non ho a disposizione una calcolatrice.
Ho un totale di 650.
Come posso usare un foglio di carta
millimetrata per trovare e
arrotondare rapidamente:

la percentuale che corrisponde a 410
e
il valore pari al 43% del totale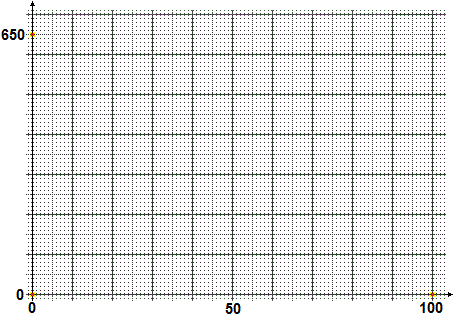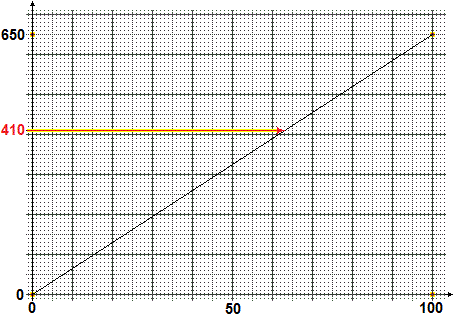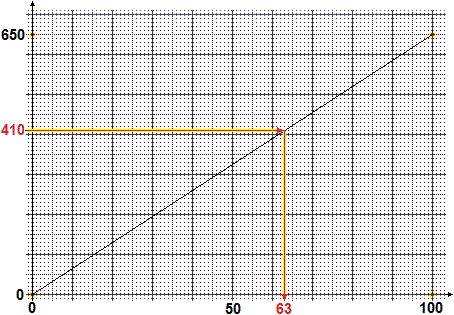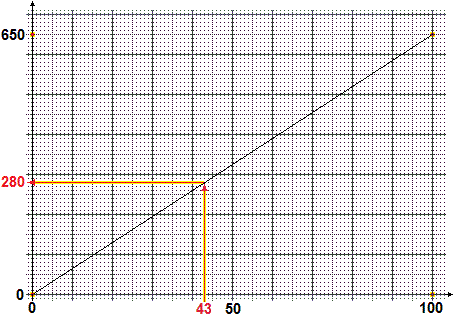 		 


 
contatori

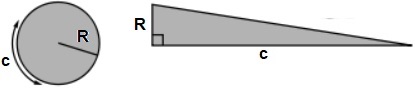
R = diametro /2    perimetro = 2·R·π     AREA = c·R/2 = π·R²
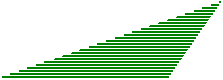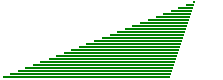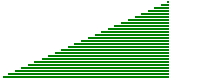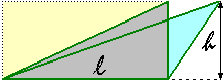
Raddrizzo man
mano i cerchietti
che formano il
cerchio.
Ottengo un trian-
golo con la base
lunga quanto la
circonferenza e
alto quanto il
raggio.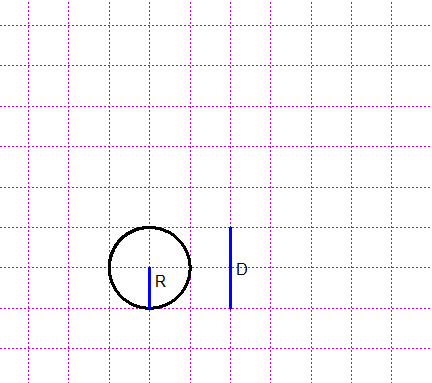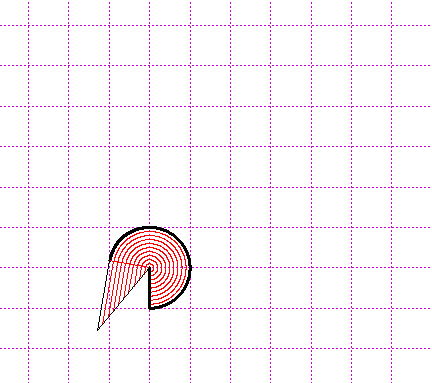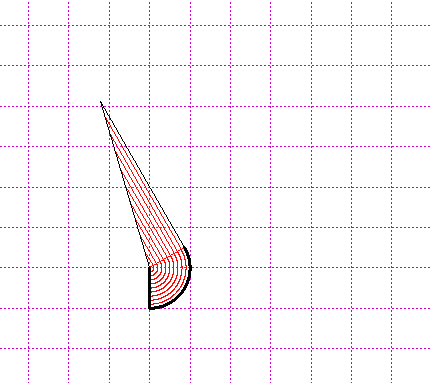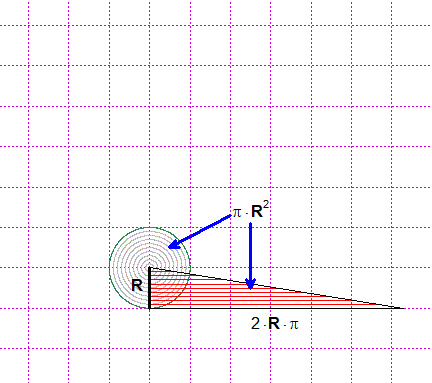 		 
 
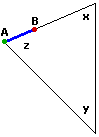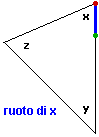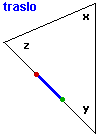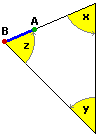
Ruoto un triangolo e un trapezio:
 
quant'è lunga l'asta?   2.709 ± 0.0005 m




 
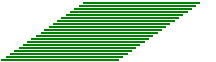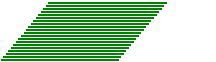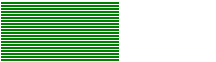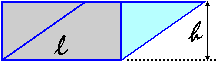l'area dei parallelogrammi e dei triangoli

     
La somma degli angoli di un triangolo è 180° se …
  Un'altra analoga rappresentazione:

     
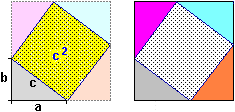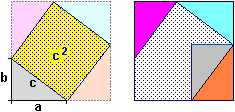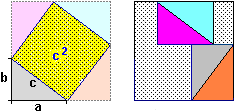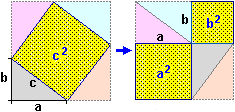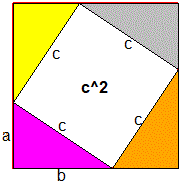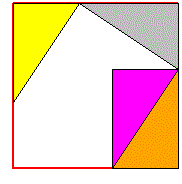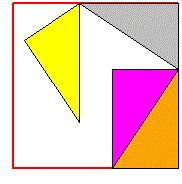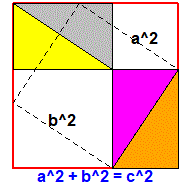… siamo in un ideale piano "piatto", ossia in cui vale la relazione pitagorica


distanza
in linea
d'aria
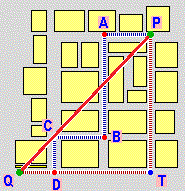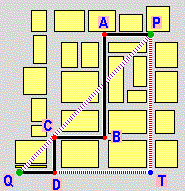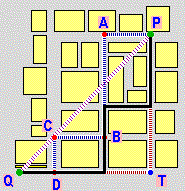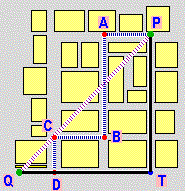→		 distanza
lungo la
strada
←
√(Δx²+Δy²) |Δx| + |Δy|

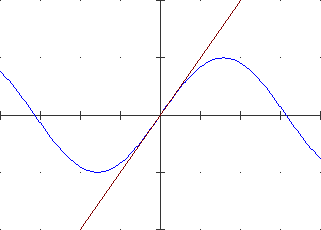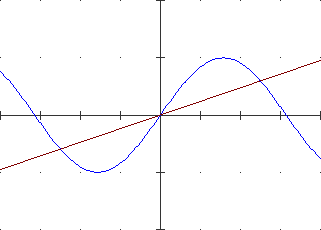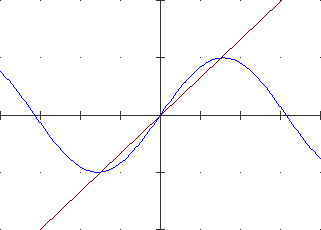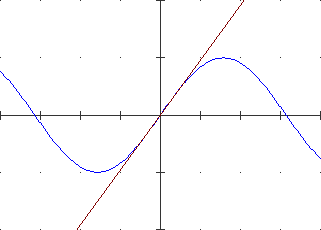
  A lato il cerchio di centro (0,0) e raggio 1.
La parte superiore è il grafico di F: x → √(1−x²).
Quant'è lungo l'arco che va da (1,0) al punto P di
ascissa −0.8?  L'approssimo con un segmento di
cui calcolo la lunghezza col teorema di Pitagora.
Poi, diviso [−8,1] in 2 parti uguali, l'approssimo
con la somma di 2 segmenti di cui calcolo la
lunghezza con lo stesso teorema. E così via.
Ottengo una successione di valori che tende alla misura esatta. Arrotondata a 7 cifre è
2.498091. Se invece di −0.8 considerassi −1 otterrei 3.141593, l'arrorondamento di π.
La lunghezza dell'arco viene considerata la misura dell'angolo α.
Ordinata e ascissa di P sono invece chiamate seno e coseno di α.

   
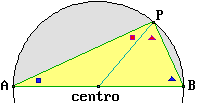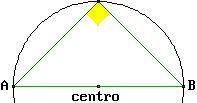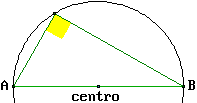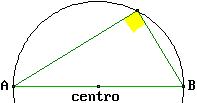
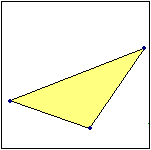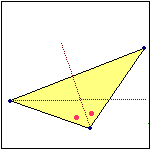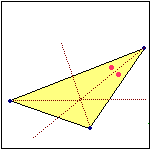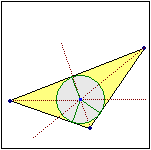
Per i vertici di ogni triangolo passa esattamente un cerchio.
Ogni triangolo inscritto in un semicerchio è rettangolo.
Dato un triangolo esiste esattamente un cerchio che ne ha i lati come tangenti.
 
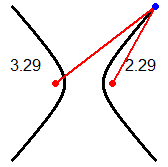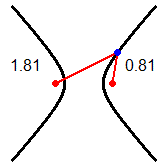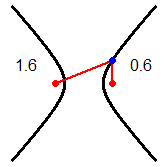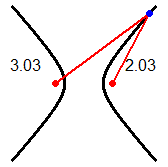
Le coniche                                                    
         
La costruzione di un asteroide:
la figura tracciata da un punto di
un cerchio che ruota su un cerchio
pi grande.		   
Sotto a un lampione acceso tengo un ombrello aperto; lo mantengo verticale; il suolo è orizzontale.
Cambia l'ombra dell'ombrello man mano che mi sposto?		   

Su una foto, dalle ombre dei bastoni riesco
a risalire alla posizione del sole?

Ma se le ombre sono parallele perché
nella foto non appaiono tali? 		  

 
Una piramide e un bastone, piantato verticalmente,
e le loro ombre.
Traccia, fuori dalla fotografia, dove è il sole. 		  

   Una casa da diversi punti di vista
Come sono fatte le figure in 3 dimensioni?



Guardo una figura tracciata
sul terreno da una distanza
di 20 m e un'altezza di 2 m.
Gli assi di riferimento sono
lunghi 10 m.
Via via mi alzo fino a 60 m.
È una parabola o un'ellisse? 		  

    Ecco come mi appare mezza iperbole, collocata nel piano xy con gli assi x ed y come asintoti, man mano che il mio sguardo si dirige più orizzontalmente, fino a che (figura D), è diretto come illustrato nella figura a destra.  Come è possibile?.  


 Guardiamo il cono con vertice in (0,0,1) e assi lunghi 2, sezionato con alcuni piani diversamente inclinati.

Cambiamo via via il punto di vista (la posizione dell'occhio O, il punto che miriamo M, la distanza D dal buco rettangolare da cui lo guardiamo)
Come appaiono le diverse sezioni se guardiamo il cono dal suo vertice con sguardo in direzione opposta all'asse z?
[ l'occhio O è in (0, 0, 1);  il punto mirato M è (0, 0, 0) ]


1:ellisse, 2:ellisse/cerchio, 3:ellisse, 4:parabola, 5:iperbole, 6:iperbole
ottenute tagliando il cono  x² + y² = z²  con
un piano che non passa per il vertice

   
I lati della figura a sinistra sono rettilinei?
Le linee orizzontali di quella a destra sono rette parallele?





Un dado "equo"

   
 
 30%

Due dadi "equi"

  
 		 30%

Un dado costruito con la carta

   
 30%
vedi qui

Lanciandone due ci si stabilizza sulla distribuzione:

  
  		 20%


   Ho 3 bastoncini della stessa lunghezza.
Li spezzo "del tutto a caso" e prendo, a
caso, una parte di ciascuno di essi.
Con quale probabilità posso costruire
un triangolo che abbia queste parti
come lati?
Non è facile risolvere questo problema.
Ma con una simulazione capisco che
la probabilità è il 50.0%.
Poi posso cercare una giustificazione
teorica ...

U = 0;
for(j in 1:7) U = U+rnd;
for(j in 1:8) U = U+rnd*rnd;
for(j in 1:6) U = U+sqrt(rnd);
for(j in 1:3) U = U+sin(rnd*3)
     Metto in U la somma Σi Ui di 24 variabili casuali numeriche indipendenti.  All'aumentare delle prove (100, 200, 400, 800, …, 12800) l'istogramma tende a stabilizzarsi su un andamento approssimativamente gaussiano. All'aumentare del numero delle variabili (comunque siano distribuite, a patto che non ve ne sia una che "prevarichi le altre") questa approssimazione migliora.     







Come varia l'altezza del punto
che ruota in funzione della
direzione del raggio?		  





Una molla ideale e una molla reale.  



x → x3–2x  
x → trunc(x)


Il profilo delle montagne
russe		 
La pendenza all'avanzare
lungo il percorso

   
La derivata di F in x0.


  
Δy/Δx = (t³−(−1))/(t(t+1)−0) = t−1 + (t+1)/(t²+t) = t−1+1/t
per t → –1 tende ad assumere il valore –3:
la tangente è dunque la retta passante per (0,–1) con
pendenza –3, ossia y = –3x–1

Un esempio di come, costruito il concetto di limite,
si può tradurre l'idea in una definizione formalizzata.		   


    
Sopra un'immagine che rappresenta una funzione continua.  Ma le funzioni continue corrispondono all'idea di essere curve tracciabili con una penna senza staccarla dal foglio?  La funzione F rappresentata a destra (F(0)=0, F(x)=cos(1/x)*x per x≠0) è continua in [−1,1] ma se mi muovo partendo dall'estremo sinistro non arriverò mai nell'origine: la strada da percorrere sarebbe infinita, e non saprei con che direzione arrivarci!

Sia F(x) = x + 3x2·cos(1/x)   se x ≠ 0,  F(0) = 0.
F'(0) = 1 > 0: il grafico oscilla tra le curve y = x + 3x2 e y = x - 3x2 e per x → 0 tende a spiaccicarsi sulla retta y = x tangente ad esse.
È un caso in cui la funzione derivata F' è definita in (-∞, ∞) ma continua solo in (-∞, 0) e in (0, ∞).		 


Il grafico di una funzione continua, non derivabile in alcun punto del dominio:
se faccio via via degli zoom trovo ovunque delle increspature
[ F(x) = ∑i=1…∞ 1/10i·h(10i·x),  h(x) = |x-floor(x+1/2)| ]







 
x
Alcuni movimenti composti

  


    XY = 9 cm
AB = 10 cm
qual è la massima inclinazione
α dell'asta AB?		   

   Sul terzo centrale di un segmento lungo 1 viene costruito un triangolo equilatero e viene cancellato il lato che sta sul segmento iniziale. E così via sui nuovi lati. La lunghezza della curva via via costruita quale valore tende ad assumere?

  Una successione di spezzate di uguali estremi (la
prima ha 4 segmenti, la seconda 8, la terza 16, …);
si appiattiscano ma sono sempre lunghe 4, e via via
meglio approssimano il segmento che ne unisce gli
estremi. Ma questo è lungo 2√2. Come è possibile?

  Il semicerchio iniziale ha diametro 1.
La lunghezza della curva via via costruita
quale valore tende ad assumere?!?



Zenone (allievo di Parmenide)

1.11111…
IR   spazio   tempo

La tartaruga ha 1 km di vantaggio sul pieveloce Achille e la sua velocità è un decimo di quella di Achille. Quando Achille ha percorso 1 km la tartaruga nel frattempo ha percorso 0.1 km e si trova a 1.1 km dalla posizione iniziale di Achille. Quando Achille, percorrendo altri 0.1 km, raggiunge questa nuova posizione della tartaruga essa nel frattempo ha percorso altri 0.01 km, e si trova a 1.11 km dalla posizione iniziale di Achille.
• In che punto Achille raggiungerà la tartaruga?
• Ma arriverà mai l'istante in cui la raggiungerà?

 

Ad Achille e alla tartaruga si unisce una mosca, che vola a 20 km/h a zig-zag tra la tartaruga, che cammina ad 1 km/h, e Achille, che la insegue a 10 km/h. Nello stesso istante in cui Achille raggiunge la tartaruga anche la mosca lo incontra. Dopo un'ora Achille si trova a 9 km dalla tartaruga. Dov'è in quell'istante la mosca?




Un raggio di luce, leggermente inclinato rispetto al piano orizzontale, entra nella "spirale" di specchi raffigurata sopra vista dall'alto. Il percorso che compie è finito (se il primo tratto rettilineo percorso nella spirale è lungo 1 m, il secondo è lungo 1/2 m, il terzo 1/4 m, il quarto 1/8 m, …, per cui in tutto il raggio percorre un tratto lungo 2 m. La luce ha velocità costante, per cui riesce a percorrere l'intero tragitto in un tempo finito. Qual è la direzione del raggio quando esce da questo "percorso guidato"?
[Non si può determinare la direzione con cui uscirebbe: l'esistenza di un ultimo specchio su cui la luce rimbalza è frutto dell'astrazione di supporre che gli specchi siano delle superfici piane senza spessore (altrimenti non potrebbero formare una spirale senza fine). In altre parole, abbiamo usato il modello astratto oltre i suoi realistici ambiti di applicazione.]


  

Mi viene assegnato un compito:
c'è una lampadina spenta, di cui accensione/spegnimento sono regolate dalla pressione di un pulsante;
dopo 3 secondi devo premere il pulsante e accendere la lampada;
dopo metà tempo (1.5 s) devo ripremere il pulsante e spegnere la lampada;
dopo metà tempo (0.75 s) devo ripremere il pulsante e accendere la lampada;
… e così via.
Dopo quanto concludo il mio compito? La lampada, in quel momento, in che stato è?

Questo e i precedenti paradossi sono "prototipi" del paradosso dei supercompiti (supertask),
ossia in cui entra in gioco il completamento di una successione infinita di compiti.


[come costruire animazioni]