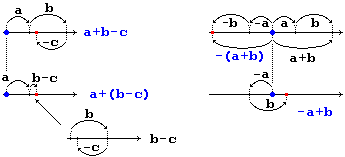
Le operazioni aritmetiche - Considerazioni didattiche
La voce Le 4 operazioni deGli Oggetti Matematici richiama il significato delle 4 operazioni (relazioni tra loro, situazioni di cui sono modello, interpretazione geometrica, …). Può essere la sintesi di tutta una serie di osservazioni e riflessioni, svolte in più occasioni all'inizio del biennio, utili a rivedere alcuni concetti e abilità di base, ed anche a creare i presupposti per successivi interventi didatticamente efficaci nei confronti degli alunni che manifesteranno difficoltà nell'impostazione delle equazioni. È utile, in particolare, discutere con gli alunni le loro strategie di calcolo mentale, mettendole in discussione se errate, proponendo alternative, … ma senza porsi l'obiettivo di imporre loro procedimenti diversi da quelli che impiegano, se corretti: persone diverse possono, per i motivi più vari, preferire seguire ragionamenti di tipo differente.
Se è il caso è bene riprendere gli elementi di base delle tecniche delle 4 operazioni, recuperando abilità di calcolo, mentali e non, spesso oscurate da "tecniche veloci" (e "volatili") su cui gli alunni sono stati fatti esercitare nei livelli scolastici precedenti (vedi qui per indicazioni sulle abilità di calcolo da recuperare; i riferimenti al calcolo monetario sono riferiti alle lire, ma sono facilmente trasferibili agli euro; vedi ad esempio gli esercizi presenti qui e qui, e nelle pagine successive).
Occorre poi tener presente l'eventuale presenza di alunni con disturbi di tipo discalculico.
La discalculia è presente in circa il 2% della popolazione, quindi in una classe di 25 alunni della scuola
di base si ha circa il 50% di probabilità di avere un alunno con alunno con tali problemi; la probabilità di averne due è
molto più bassa, circa il 25%; di averne tre è circa del 10%. Un insegnante di scuola elementare nel corso della sua
carriera dovrebbe incontrare circa 5 alunni con disturbi discalculici (spesso, per incompetenza di chi fa queste diagnosi,
vengono segnalati come casi discalculici situazioni che non rientrano in questo ambito). Un insegnante di scuola media inferiore
ne potrebbe incontrare una decina. Per i docenti di scuola superiore il numero dipende dal tipo di scuola in cui
si insegna.
Che fare in queste situazioni? Innanzi tutto occorre segnalare che la discalculia si manifesta in alunni con intelligenza
normale e senza disturbi di tipo neurologico. Occorre quindi, a partire dalla scuola di base, come con gli altri alunni,
far riferimento a tutte le situazioni della vita reale in cui si usano i numeri, far riferimento ad algoritmi in cui
sia trasparente il significato del procedimento e, in particolare con loro, appoggiarsi subito a sussidi di tipo
tecnolgico per lo svolgimento delle attività di calcolo, limitandone inizialmente l'uso da parte degli altri alunni.
Si possono impiegare le usuali calcolatrici o calcolatrici
presenti nel software, come quelle a cui si può accedere da qui;
si può ricorrere al "traduttore" di Google (vedi)
in cui si possono scrivere numeri e operazioni (come: 7.5 1500 12% 5000000 3/4)
e ascoltare la loro lettura; si può anche (come suggerito dal sito internazionale che si occupa della
discalculia) usare WolframAlpha (vedi qui,
clicca poi su Elementary Mathematics, Arithmetic). Le difficoltà di tipo discalculico sono
in buona parte legate a problemi di memorizzazione (analoghi per alcuni aspetti a difficoltà simili
che possono subentrare in alcune persone in seguito a incidenti o a piccoli ictus) che non compromettono
la comprensione delle attività matematiche se ci si appoggia - come si può fare ormai da vari decenni -
all'uso del computer. È, ovviamente, opportuno che gli insegnanti stimolino questi alunni, sin dai
primi anni di scuola, ad usare opportunamente i mezzi di calcolo.
Un disturbo per molti versi simile (e leggermente più frequente, circa due volte la discalculia) è la dislessia, ossia la difficoltà nel leggere e a volte scrivere le parole che si manifesta in genere con la trasposizione e l'inversione di gruppi di lettere. L'uso del computer è, evidentemente, di grande aiuto anche per far fronte ai problemi che essa genera. Si può ricorrere,
in modo simile a quanto detto per la discalculia, a Google, ai programmi di scrittura gratuiti (come OpenOffice, LibreOffice, …) e ai loro controllori ortografici (che propongono alternative
a quanto digitato). La stessa battitura dei testi sul computer, e l'osservazione di quanto si sta scrivendo, e la possibilità di correggere quanto scritto, è di per sé
di aiuto per chi ha problemi di questo genere.
Le attività sulla linea dei numeri, in particolare quelle che coinvolgono i numeri negativi,
sono assai utili per consolidare (anche attraverso la riproposizione di esercizi simili)
l'abitudine ad appoggiarsi alla (immagine mentale della) linea dei numeri. È importante introdurre
correttamente i numeri negativi, non far usare regolette (foriere di misconcezioni) come "−" per "−" fa "+",
non far mettere il segno "+" davanti ai numeri positivi, ….
Errori frequenti frutto di queste misconcezioni sono, ad es., quello di trasformare
Sulle prime tracce dell'uso dei numeri negativi da parte dei babilonesi (a cui si accenna nella nota finale della voce "le 4 operazioni") si possono trovare considerazioni in vari libri di Martin Gardner e in molti articoli scientifici, ad esempio qui.
È utile interpretare gli errori o le difficoltà di calcolo numerico, scritto o mentale, degli alunni, farne esplicitare le origini, far fare verifiche delle proprietà usate erroneamente (o di quelle non usate) su semplici casi, ricorrere a modelli interpretativi di tipo geometrico per generalizzare esempi numerici, come i seguenti (il primo illustra una proprietà utilizzabile, il secondo un errore):
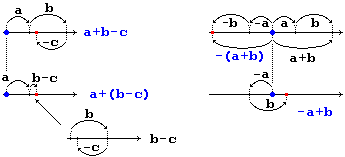
|
Le operazioni con numeri negativi sono facilmente intepretabili, se introdotte nel modo descritto nella voce
le 4 operazioni. Ad esempio, nel caso della formula |
 |
Queste riflessioni/attività dovrebbero facilitare l'interiorizzazione delle trasformazioni a cui può essere sottoposto un termine numerico da parte degli alunni che incontrano difficoltà di fronte a ragionamenti più formalizzati.
Alla voce Struttura dei termini sono illustrate rappresentazioni grafiche della struttura dei termini, anch'esse introducibili, in modo operativo, a partire dalle prime attività del biennio.
Attività sul significato delle operazioni e sulla loro interpretazione geometrica
possono essere suggerite anche da vari esercizi presenti nell'"eserciziario" (argomento "operazioni", parti 0, 1 e 2)
da cui si può accedere dalla sezione
 .
.
Nota. Le operazioni aritmetiche sono le prime funzioni numeriche
con cui si ha a che fare nella vita scolastica. Nella voce Funzione-1 le operazioni vengono inquadrate in questo
concetto più generale. Il termine operazione in matematica viene usato
in diversi modi nelle varie aree della disciplina. In genere indica una funzione (o applicazione)
descritta attraverso un procedimento (in senso lato, non necessariamente "meccanico") e che assume un rilievo particolare nella
caratterizzazione di un certo tipo di struttura matematica o di un particolare settore della
matematica; il simbolo funzionale utilizzato per descriverla viene chiamato operatore,
ma a volte con questo termine si indica la funzione stessa. Esempi: l'unione tra due insiemi
(è un'operazione che a due insiemi associa un altro insieme, e che dà
una certa struttura algebrica alla classe dei sottoinsiemi di un certo insieme), la composizione
di funzioni, il passaggio al limite, la derivazione e l'integrazione, i prodotti scalare e vettoriale,
… Vedi qui per qualche nota ulteriore.
Negli Oggetti Matematici "operazioni" viene, inizialmente, usato essenzialmente per descrivere funzioni a input
e output in uno stesso insieme di cui viene studiata la struttura algebrica rispetto ad esse,
con una intuitiva generalizzazione del concetto di operazione artimetica. Si vedano
le voci richiamate nelle righe seguenti di queste "considerazioni didattiche".
Una riflessione più generale sulle operazioni viene svolta alla voce Strutture numeriche. Le loro proprietà sono approfondite alla voce Termini equivalenti. Nella voce Calcolo approssimato sono sistemate le riflessioni sul modo in cui si opera con valori approssimati.
Nello sviluppo dell'insegnamento della matematica nelle sue varie aree è importante via via mettere in luce (in modo occasionale, senza soffermarsi troppo) analogie e differenze tra modi in cui si opera sui numeri e modi in cui si opera su altri oggetti matematici. Queste considerazioni sparse possono costruire gradualmente il terreno su cui, poi, tra la fine del biennio e l'inizio del triennio, impostare (nelle classi non troppo "difficili") una sistemazione più organica, come quella presentata nella voce Strutture numeriche e non.