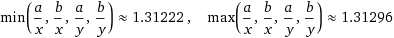
I numeri reali
• Che cosa sono i numeri reali?
• Una loro definzione costruttiva "corretta"
• Una definizione assiomatica
• La crisi della definizione "geometrica"
• L'approccio di Dedekind (sezioni)
• L'approccio di Cantor (successioni)
• R esiste?
• Concludendo
• Il numero 27.(04) = 27.040404... è generabile con il diagramma di flusso qui a destra: Generalizzando si ottiene la def. di numero periodico. |
(1) scrivi "27." (2) scrivi "24" (3) vai a (2) |
se vuoi ———> scrivi una seq. ———> scrivi —————> scrivi —————>
scrivi "-" finita di cifre "." | una cifra |
| |
<—— stai scrivendo <——
un NUMERO REALE | |
dove dove le sequenze finite di cifre siano state definite con questo diagramma: | |
scrivi una cifra ———> vuoi continuare? —— no ——> hai scritto una SEQUENZA
| | si` FINITA DI CIFRE
<—————————————————— | |
Questo approccio pone alcuni problemi (che sono legati a questioni che, al di là dell'approccio scelto per introdurre i numeri reali, devono comunque essere affrontate):
(a) come definire l'eguaglianza tra numeri reali (cioè quando due espressioni illimitate devono essere considerate uguali "come numeri")?
(b) la limitatezza (avere periodo 0) di un numero dipende dalla base di rappresentazione?
(c) la periodicità è una proprietà dei numeri o dipende dalla base?
(d) come definire le operazioni tra numeri reali?
• Vediamo come affrontare le questioni (a)-(d):
(a) Tra 3.7999... e 3.8000..., pensati come posizioni sulla retta o come
misure, non ci sono altri numeri; tale espressioni decimali indicano la stessa
posizione o la stessa misura; quindi sono da intendere uguali come numeri;
del resto noi sappiamo che, ad es., 0.999... è il limite della successione
0.9, 0.99, 0.999, 0.9999, ..., ovvero di
Più in generale, due espressioni decimali
illimitate sono uguali come numeri se, tolti gli eventuali zero iniziali,
esse coincidono o l'una ha periodo 9, l'altra ha periodo 0 e le cifre che
precedono il periodo costituiscono due numeri naturali il primo inferiore di
un'unità rispetto al secondo: 3.7999... = 3.8000... in quanto 37+1=38.
Questi aspetti sono discussi nella voce I numeri degli Oggetti Matematici.
(b) La limitatezza dipende dalla base: 1/3 (uno diviso tre) in base dieci non
ha periodo 0 (diventa 0.333...) mentre in base 3 diventa: 0.1000...
Invece 1/2, che in base dieci ha periodo 0 (vale 0.5000…) in base 3 diventa
0.111… come posso verificare eseguendo la divisione moltiplicando via via i
resti per 3 (che equivale a 10 in base 3) invece che per dieci.
Infatti gli usuali algoritmi delle operazioni valgono qualunque sia la base
di rappresentazione (il ruolo che ha 9 in base dieci viene assunto da 2 in
base 3, da 1 in base 2, da 4 in base 5, ...
La definizione di numero e di eguaglianza di numeri data sopra vale anche usando altri sistemi di cifre: in base 3 considereremo uguali due espressioni aventi una periodo 2 e l'altra periodo 0 e tali che ...
(c) La discussione precedente chiarisce che la periodicità non dipende dalla
base (considerando, come si deve fare, periodici i numeri con periodo 0).
Questi aspetti sono discussi nelle voci Basi di rappresentazione e
Strutture numeriche.
(d) In questa impostazione le operazioni possono essere definite come
"limiti": se x(n) e y(n) sono le approssimazioni di x e y (per troncamento o per
arrotondamento) al posto −n, x+y, x·y, ... sono i limiti di x(n)+y(n),
x(n)·y(n), ... (definendo le operazioni tra decimali limitati mediante gli
usuali algoritmi).
Il concetto di limite può essere introdotto come:
migliorando opportunamente la precisione dei fattori posso conoscere con la
precisione che voglio x+y, x·y, … . Il programma R
(o calcoli analoghi fatti con una calcolatrice) possono motivare (a livello di biennio)
queste considerazioni. Ecco ad es. il calcolo
di
x1 = 4.1; x2 = 4.2; y1 = 3.1; y2 = 3.2 m = min(x1/y1, x1/y2, x2/y1, x2/y2) M = max(x1/y1, x1/y2, x2/y1, x2/y2) c(m, M, M-m) # 1.28125000 1.35483871 0.07358871 x1 = 4.12; x2 = 4.13; y1 = 3.14; y2 = 3.15 m = min(x1/y1, x1/y2, x2/y1, x2/y2) M = max(x1/y1, x1/y2, x2/y1, x2/y2) c(m, M, M-m) # 1.307936508 1.315286624 0.007350116 x1 = 4.123; x2 = 4.124; y1 = 3.141; y2 = 3.142 m = min(x1/y1, x1/y2, x2/y1, x2/y2) M = max(x1/y1, x1/y2, x2/y1, x2/y2) c(m, M, M-m) # 1.3122215150 1.3129576568 0.0007361418 x1 = 4.1231; x2 = 4.1232; y1 = 3.1415; y2 = 3.1416 m = min(x1/y1, x1/y2, x2/y1, x2/y2) M = max(x1/y1, x1/y2, x2/y1, x2/y2) c(m, M, M-m) # 1.3124204227 1.3124940315 0.0000736088 |
Si vede che al dividersi per 10 della indeterminazione dei fattori tende a dividersi per 10 anche la indeterminazione del risultato. Nel triennio queste considerazioni intuitive possono essere meglio formalizzate.
Si potrebbe usare anche WolframAlpha mettendo ad es.:
a=4.123;b=4.124;x=3.141;y=3.142;min(a/x,a/y,b/x,b/y);max(a/x,a/y,b/x,b/y)
otterrei:
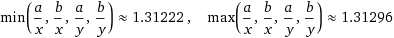
[per inciso, con WolframAlpha potrei ottenere tutte le cifre che voglio: sqrt(17)/pi = 1.312425 282414 104560 953767 228313 214383 665881 283501 767457 374502 485339 902649 225842 865447 797005 797566 593430 459786 946574 84222…]
• Quali sono altri modi per introdurre i numeri reali?
Come sono introdotti all'università i numeri reali?
Nei corsi di analisi matematica in genere i numeri reali vengono introdotti assiomaticamente (anche se, a volte, non si pretende di averli definiti, ma, "onestamente", si dice che se ne sono sintetizzate le proprietà, precisando che essi esistono e si possono costruire, ma che per semplicità, invece di dimostrarne le proprietà, le si sono assunte come assiomi). Poi viene introdotto l'insieme dei numeri naturali N, ad esempio come l'intersezione di tutti i sottoinsiemi A di R (insieme dei numeri reali) t.c. 0 è in A e se x è in A anche x+1 è in A. L'insieme degli interi Z ("Z" è l'iniziale della parola tedesca che significa "numero": vedi) viene introdotto come {x in R / x è in N o −x è in N}, l'insieme dei razionali Q è introdotto come {x in R / esistono y in Z e z in N−{0} t.c. x = y/z}.
La struttura (R,+,0,*,1,R+) (+ e * operazioni binarie, 0 e 1 elementi, R+ sottoinsieme, o relazione unaria) può essere descritta così:
− è un campo:
(R,+,0) e (R-{0},*,1) sono gruppi commutativi,
(R,*,1) è un monoide [∀x,y,z ∈ R (x*y)*z = x*(y*z)] con identità,
∀x,y,z ∈ R x*(y+z) = (x*y)+(x*z)
− ordinato:
∀x,y ∈ R+ (x+y ∈ R+ e x*y ∈ R+),
se x ≠ 0 (x ∈ R+ o −x ∈ R+),
0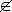 
R+ (si pone x < y come abbreviazione di y−x sta in R+)
− e completo:
∀x,y ∈ R+ è possibile addizionare un numero finito di volte x per ottenere un numero maggiore di y (proprietà archimedea),
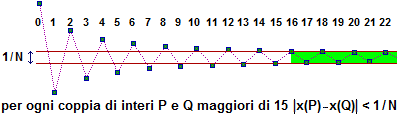
ogni successione di Cauchy di elementi di R converge.
[ x(.) soddisfa la condizione di Cauchy se per ogni N numero intero positivo esiste K tale che per ogni P e Q interi maggiori di K x(P) dista da x(Q) meno di 1/N, ossia (vedi figura sotto) gli elementi della successione di posto maggiore di K stanno tutti entro una striscia ampia 1/N ]
Problemi (specie se non si fa la "onesta" precisazione):
(A) Chi mi garantisce che R sia unico? Qui (e nel caso della presentazione assiomatica dello spazio euclideo) vogliamo definire/individuare assiomaticamente un "oggetto" matematico. È una situazione diversa dalla definizione assiomatica dei "concetti" di gruppo, campo, ...
(B) Chi mi garantisce che R esista? (l'esistenza di un modello degli assiomi, per altro, mi garantirebbe che gli assiomi non presentano contraddizioni)
Ad (A) si può rispondere dimostrando che due strutture che soddisfino gli
"assiomi di R" sono isomorfe (anche se, a essere rigorosi, anche questa
"unicità a meno di isomorfismi" è relativa: dipende da come è stata scelta
la teoria degli insiemi in cui si opera). E a (B)?
Ecco un breve panorama storico.
• L'analisi si appoggiava alla geometria: i numeri reali erano intesi come grandezze geometriche, il significato delle operazioni era fondato su considerazioni geometriche. Somma e differenza erano ricondotte alla somma e alla differenza di segmenti. La divisione veniva introdotta come rapporto tra segmenti. Moltiplicazione: se a e b sono le misure di due segmenti S1 e S2 rispetto all'unità di misura OU, a·b è la misura del segmento QT costruito nel modo
seguente: |  |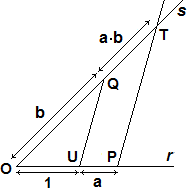
Fino agli inizi del XIX secolo ci si accontentava di questa impostazione. Ma chi ci garantisce che esista un modello per gli assiomi della geometria euclidea?
Questo problema non turbava i matematici di allora: gli assiomi della geometria venivano intesi come una descrizione dello spazio fisico.
La matematica aveva nella fisica i suoi fondamenti (analogamente non ci si preoccupava di definire matematicamente che cos'è una funzione:
veniva intesa come la descrizione di una "legge" che lega una grandezza fisica a un'altra grandezza). Solo tra la fine del XIX e l'inizio del XX secolo, messa nitidamente a fuoco
la necessità di dimostrare la non contraddittorietà degli assiomi della geometria euclidea, si raggiunge questo obiettivo dimostrando che
R3 (punti: terne di numeri reali, piani: equazioni lineari, distanza come funzione
R3xR3 → R, ...) ne è un modello.
Ma a questo punto ci troviamo di fronte nuovamente al nostro problema (B).
Il problema della definizione di R, invero, lo avevano già affrontato (intorno al 1870) Dedekind e, separatamente, Cantor. Non lo inquadravano nell'ambito delle questioni a cui abbiamo accennato sopra (esistono modelli degli assiomi di R e degli assiomi della geometria euclidea?), che sono state formulate successivamente, ma avevano l'obiettivo di dare una costruzione di R autonoma dalla geometria, a partire dai numeri naturali. Questo obiettivo viene usualmente descritto come "aritmetizzazione dell'analisi" ed era, in qualche modo, una prosecuzione del lavoro di precisazione dei concetti dell'analisi infinitesimale (che superasse il ricorso all'idea intuitiva di infinitesimo) avviato da Cauchy e da Bolzano (sviluppi di questo lavoro saranno la messa a punto del concetto di funzione e la trattazione dei numeri transfiniti, che Cantor affronterà dando origine alla teoria degli insiemi).
• Vediamo, dunque, la costruzione di R a partire da N, assunto come noto (e inteso come struttura (N,+,0,*,1)), seguendo (con un linguaggio più "moderno" ) più o meno l'itinerario di Dedekind. Vedremo, successivamente, l'approccio di Cantor, più semplice e intuitivo, e basato su un approccio "costruttivo" (che non ricorre ad alcuni aspetti della teoria degli insiemi fondazionalmente meno "sicuri": chi vuole approfondire veda gli "appunti" richiamati alla fine del documento); ad esso è molto simile l'approccio da noi seguito. Come vedremo, l'approccio di Dedekind è piuttosto complesso. Nei libri di testo più diffusi, in cui viene riproposto, è descritto in modo in genere errato. Per altro una descrizione corretta non sarebbe comprensibile, né tecnicamente né culturalmente, da parte degli alunni (come vedremo tra poco). E un approccio "alla Dedekind" non ha niente a che fare con quello usato per introdurre il concetto di retta nelle presentazioni assiomatiche della geometria messe a punto nel secolo scorso, e a cui facevano riferimento un tempo i libri di testo (vedi, se sei interessato; guarda in particolare, usando i link in fondo al documento, l'assioma 14 dell'Enriques-Amaldi e l'assioma 1 del Prodi).
# Z viene introdotto come N×N; l'idea è quella di introdurre i numeri interi
come differenze tra numeri naturali: le coppie (7,5), (3,1), ... hanno differenza "positiva" pari a 2, le coppie (0,4), (2,6), ... hanno differenza "negativa" pari a −4.
Così come consideriamo uguali come numeri naturali le diverse espressioni 3, 03, 003, ..., così ci poniamo il problema di quando
due coppie (x,y) e (z,w) (x,y,z,w∈N) siano da considerate uguali come numeri interi.
Per ricondursi a (N,+,0) possiamo porre:
(x,y) =Z (z,w) sta per: x+w = y+z
(idea: sottrazione come operazione opposta dell'addizione: x–y=z–w sse x+w=z+y).
=Z è una buona definizione di uguaglianza?
Si può verificare facilmente che è riflessiva, simmetrica e transitiva.
Possiamo definire l'opposto di un numero intero (m,n) così: –(m,n) sta per: (n,m).
È una buona definizione? Cioè è indipendente dalla coppia con cui
descriviamo il numero? ossia se (p,q) =Z (m,n) ho che –(p,q) =Z –(m,n)?
Anche questa verifica è facile.
Per l'addizione l'idea è semplice: (m,n) +Z (p,q) sta per: (m+p,n+q).
È una buona definizione?
Se (*): (x,y) =Z (m,n) e (z,w) =Z (p,q) devo avere:
Idea per la moltiplicazione: (m,n) sta per quello che vogliamo comportarsi
come m–n;
(1) (r,s)·(p,q) = (rp+sq,rq+sp), (m,n)·(p,q) = (mp+nq,mq+np); quindi:
(2) (r,s)·(p,q) = (m,n)·(p,q) sse rp+sq+mq+np = rq+sp+mp+nq
(3) poiche' (r,s) =Z (m,n), r+n = s+m, quindi:
(4) rp+sq+mq+np = (r+n)p+(s+m)q = (s+m)p+(r+n)q = rq+sp+mp+nq
(5) da (2) e (4) posso concludere che: (r,s)·(p,q) = (m,n)·(p,q)
In maniera analoga si ha che: Se (r,s) =Z (p,q), (m,n)·(p,q) = (m,n)·(r,s)
# Q viene introdotto come Z×Z; (x,y) =Q (z,w) sta per (scrivendo = invece di =Z e · invece di ·Z) x·w=y·z (si noti l'analogia formale con la definizione di =Z; ora l'idea è quella di divisione come operazione opposta della moltiplicazione). Poi si definiscono addizione, ...
NOTA. Ai nostri giorni gli "algebristi" soppiantano la parola "uguaglianza" con la parola "relazione di equivalenza" e, ad esempio, considerano come numeri interi la classi di equivalenza indotte da ==Z, riconducendo così l'eguaglianza tra numeri interi all'uguaglianza tra insiemi. La sostanza non cambia.
# R viene introdotto come insieme delle SEZIONI "](" di Q, cioè come insieme
delle coppie (A,B), con A e B sottoinsiemi di Q, tali che:
(A∪B) = Q, (A∩B) = ∅, ∀x∈A ∀y∈B x<y, B non ha primo elemento;
o, equivalentemente, considerando solo la parte destra delle sezioni, come
INTERVALLI "(" di Q: intervalli finali senza primo elemento, pensabili come
intersezioni con Q di intervalli di R del tipo (a,∞).
[ Dato un insieme ordinato (E,<), un "intervallo" di E è un sottoinsieme I di E tale che: (x,y∈I, x<z<y) → (z∈I); un intervallo "finale" è un sottoinsieme I tale che: (x∈I, x<y) → (y∈I); un sottoinsieme I è "senza primo elemento" se: (x∈I) → (∃y∈I t.c. y<x) ]
Ad es. √2 verrebbe rappresentato con la sezione (A,B) con A = {x in Q /x·x ≤ 2}, B = {x in Q / x·x > 2} (A: numeri razionali che approssimano √2 per difetto, B: numeri razionali che lo approssimano per eccesso); ovvero, più semplicemente, con l'intervallo {x in Q / x·x > 2}. Scegliamo la seconda strada.
Se x è I e y è J l'eguaglianza x =R y viene ricondotta all'eguaglianza
tra I e J.
Come x +R y si prende K = {a+b / a∈I, b∈J}.
Come –x ("–": negazione in R) si prende K = {–p / p non è in I, esiste q
non in I t.c. p<q }
[ La clausola "esiste q non in I t.c. p<q" serve per togliere l'eventuale
primo elemento, in modo da avere un intervallo "(". Idea: se x è 1.333...,
cioè I =
Come x ·R y se I e J non contengono 0 (cioè se x e y sono
"non negativi") si prende K =
Poi occorre trovare anche il "trucco" per definire <R, e occorre
verificare che queste sono "buone definizioni".
Verifichiamolo solo per la "addizione" +R, ossia verifichiamo che K è un intervallo "("
[x è I e y è J, K è
K è "(" se è senza 1º elemento e è finale.
(i) K è senza 1º elemento, cioè x∈K → ∃z < x
Se x è in K, esistono a in I e b in J t.c. x = a+b;
poiché I e J sono "(", sono senza 1º el., cioè esistono z1 e z2 con
z1<a e z2<b; per le proprietà di Q si ha che
z1+z2<a+b. Ho quindi trovato
z t.c.
(ii) K è finale: x in K & x<y → y in K (cioè vi sono
a1,b1 t.c. ...)
Sia x=a+b (come sopra); da x<y ho a<y–b da cui, per la densità di Q,
esiste a1 t.c. a<a1<y–b.
Poiché I è finale a1 sta in I. Posto b1=y–a1, ho
b1>b, e quindi (essendo J finale) b1 sta in J. Quindi y (=a1+b1) sta in K.
• Cantor definì, invece, i numeri reali come successioni di numeri razionali soddisfacenti la condizione di Cauchy (vedi), definì due successioni x e y uguali "come numeri" se x(n)–y(n) → 0 per n → ∞, definì x+y come (x+y)(n) = x(n)+y(n), ... . La condizione di Cauchy è infatti equivalente (in R) all'esistenza del limite e, quindi, permette di individuare l'insieme di tutte le successioni convergenti senza menzionare i numeri a cui esse convergono, che, appunto, costituiscono l'insieme dei numeri reali.
Potremmo anche dire che, come il passaggio da N a Z permette di rendere sempre definita la sottrazione, il passaggio a Q permette di rendere sempre definita la divisione per numeri diversi da 0, così il passaggio a R consente di determinare il limite di ogni successione di Cauchy.
Sostanzialmente, l'approccio discusso all'inizio si rifa alla impostazione di Cantor: l'unica differenza è che al posto di tutte le "successioni di Cauchy" si sono prese solo le successioni x(.) tali che per ogni numero naturale n x(n) sia l'approssimazione per troncamento alla cifra di posto –n di x(n+1); ad es. √2 è rappresentato dalla successione x(0)=1, x(1) = 1.4, x(2) = 1.41, x(3) = 1.414, ...; 3 è rappresentato sia da x(0) = 2, x(1) = 2.9, x(2) = 2.99, ... che da x(0) = 3, x(1) = 3.0, x(2) = 3.00, ...
• Ritornando al problema (B) posto all'inizio, tutto sembrerebbe ricondotto
ai numeri naturali: definire assiomaticamente i numeri naturali e
dimostrare che questo sistema di assiomi ha un modello o dimostrare in altro
modo che non è contraddittorio (usando metodi dimostrativi più elementari
delle argomentazioni aritmetiche, altrimenti entreremmo in un circolo
vizioso). Questo era, grosso modo, l'obiettivo che aveva definito Hilbert
nei primi anni del XX sec., ma Gödel, con un famoso teorema (1931), ha
messo praticamente la parola "fine" a questi tentativi.
Non abbiamo, dunque, prove "assolute" della coerenza degli assiomi di R
e degli assiomi della geometria euclidea, ma abbiamo solo la prova che se
uno dei due sistemi di assiomi è coerente allora è coerente anche l'altro
(dimostrazione "relativa" di coerenza).
Ci si può accontentare di prendere per buono il concetto intuitivo di
successione e cercare di "costruire" la matematica sulla base di questo,
attraverso procedimenti "algoritmici", o si possono assumere come
presupposto la consistenza della teoria dei numeri naturali (basando questa
assunzione sull'esperienza secolare degli uomini nel campo dei calcoli e
delle dimostrazioni relative ai numeri naturali) e la possibilità di
lavorare con enti infiniti.
Osserviamo, che, ormai, il dibattito sui "fondamenti della matematica" non
è più volto alla ricerca di definizioni "assolute", alla ricerca di presupposti metafisici o "prematematici", ma è una riflessione più strettamente
legata all'analisi del modo in cui lavorano i matematici, del ruolo di linguaggi formali e metodi dimostrativi, dei problemi legati ai passaggi tra
teorie matematiche diverse (la traduzione della geometria nell'algebra, un
problema dei numeri reali affrontato nell'ambito dei numeri complessi, un
problema di aritmetica elementare affrontato topologicamente, la dimostrazione della consistenza di una teoria svolta in un'altra teoria, ...).
La natura degli "oggetti matematici" non si può definire cercando l'idea
platonica giusta o la realtà concreta fondante, ma, più laicamente, il
significato degli oggetti della matematica si chiarisce attraverso la loro
rappresentazione in linguaggi e teorie diverse, attraverso la possibilità di
dare interpretazioni diverse dello stesso formalismo, attraverso
l'individuazione di analogie e differenze di fondo, attraverso processi di
successiva delimitazione/estensione e raffinamento dei concetti (intuitivi o
più o meno formalizzati) che possono anche biforcarsi, ... . Questa è la
matematica dei "matematici", sia la matematica "pura" che la matematica
"applicata".
A queste problematiche dovrebbe, indirettamente, riferirsi anche l'insegnamento della matematica (nelle scelte di come impostare l'introduzione dei
concetti, la loro formalizzazione, le dimostrazioni,...).
• Concludendo, l'approccio descritto nei primi due paragrafi (Che cosa sono i numeri reali? e Una loro definzione costruttiva "corretta") è un approccio semplice e corretto per introdurre i numeri reali. Non ha alcun senso, in un percorso didattico per la scuola superiore, scimmiottare l'approccio di Dedekind quando non si può (sia per difficoltà concettuali che per tempo didattico richiesto) svilupparlo in modo appropriato, e non si hanno gli strumenti per collocarlo storicamente e filosoficamente.
[ Per approfondimenti su alcuni di questi aspetti si può vedere la sezione 4
di una raccolta di appunti su fondamenti della matematica e concetto di
algoritmo ]