Sui "polinomi"

In matematica (come sappiamo dai nostri studi universitari e da un qualunque sito internet attendibile, ad esempio Wolfram) ...

Una funzione F: x → a_n xⁿ + a_n–1 x^n–1 + …a₂ x² + a₁ x + a₀ con  a_n ≠ 0 viene chiamata funzione polinomiale di grado n; a_i viene chiamato coefficiente di grado i.
I coefficienti possono essere costanti, variabili o termini più complessi (purché non contenenti x).
L'equazione F(x) = 0 viene chiamata equazione polinomiale di grado n.
Il termine F(x) viene chiamato polinomio in x di grado n.

Come la parola poligono deriva dalle parole greche polís (molto) e gonia (angolo), a mo' di "figura dai molti angoli", così la parola polinomio deriva dalle parole greche polís e ónoma (nome, espressione), a mo' di "espressione costituita dalla somma di molte espressioni". Si parla anche di trinomio, binomio e monomio per indicare un polinomio che è somma di 3, 2 o 1 termine, cioè in cui solo 3, 2 o 1 tra gli a_i sono diversi da 0.

Per parlare di grado di un polinomio occorre specificare o che sia chiaro dal contesto qual è la variabile a cui riferirlo. Ad esempio A+A·B³ può essere pensato come un polinomio (in particolare, un binomio) di 3° grado in B, ma, trasformato in A·(1+B³), può essere considerato anche un polinomio (in particolare, un monomio) di 1° grado in A, o può essere considerato come un polinomio di grado 0 in y: la variabile y non compare in esso, quindi rispetto ad y è una costante. La variabile rispetto alla quale un termine viene considerato un polinomio a volte viene chiamata indeterminata.

Nell'ambito delle studio delle funzioni a due input si considerano anche i polinomi in 2 (o più) indeterminate. Ad es. (x,y) → k x³·y² + x·y + y/4 + π è una funzione polinomiale a 2 input di grado 5; i gradi vengono calcolati sommando le potenze a cui sono elevate le due indeterminate, x e y.

Nei libri di testo (solo) italiani (solo) del primo biennio molto spesso si trova ...

Si chiama monomio ogni funzione che consiste in un prodotto di fattori numerici e di potenze aventi come basi lettere e come esponenti numeri naturali.
Si chiama polinomio una somma di due o più monomi.

Ma ...

• Il polinomio in x   x² / k + x   non rientra nella definizione del libro.
Ad essere rigorosi non rientrerebbe neanche:
3x  (non è la somma di due monomi, a meno che non lo trasformi in 0+3x)
e neanche  −x    x²    x−a  … (a meno che non si ammettano opportune manipolazioni algebriche).

• Viene confuso grossolanamente il concetto di funzione con quello di termine:
il termine x+7 è diverso dalla funzione A → A+7 !

• Poi, nel triennio, non terrà alcun conto di tutte queste definizioni: si considereranno solo i polinomi in x, e anche quelli in cui compaiono altre lettere sotto al segno di frazione o all'interno di una radice quadrata o …!

È attraverso "definizioni" errate di questo tipo (in genere date prima di "introdurre" i concetti) che si distrugge, sistematicamente, l'attenzione dei ragazzi alle definizioni e la comprensione del ruolo di esse.

Quando e perché studiare i polinomi?

In molti libri di testo italiani del primo biennio superiore (ed anche della scuola di base) vengono studiati i "polinomi" mettendone a punto proprietà che sono invece dei numeri:  la possibilità di riordinare una somma o un prodotto, la proprietà distributiva, …. E viene escluso lo studio di funzioni di base, essenziali per la rappresentazione dei più comuni fenomeni reali (come ad esempio x → a+b/x).
Perché studiare le funzioni polinomiali?

Perché alla fine del biennio (dopo aver avviato lo studio delle funzioni in generale) se ne possono mettere a fuoco alcune caratteristiche che le distinguono dalle altre funzioni:

• perché tra i polinomi in una indeterminata (i "polinomi", non la cosa descritta nell'esempio iniziale) è possibile definire, in analogia con i numeri interi, una divisione con resto;
• perché vale il teorema del resto  (non la "regola del resto"!!! - vedi);
• perché (in conseguenza di esso) sappiamo che il numero delle soluzioni di una equazione polinomiale non supera il grado;
• e perché con le funzioni polinomiali possiamo approssimare le altre funzioni (e "capire" come è possibile che un computer riesca a calcolare seno, esponenziale, …).

Sono solo queste le cose essenziali relative ai polinomi su cui ha senso soffermarsi (alla fine del biennio e nel triennio).

Nota.  I polinomi in 2 o più indeterminate sono fattorizzabili in modo univoco  [prova a introdurre in WolframAlpha ad esempio factor x^3+x^2*y-x^2-x*y:  ottieni x(x-1)(x+y)],  e, quindi, tra due di essi si può trovare un massimo comune divisore.  Ma per essi non si può definire, in generale, una divisione con resto  (in cui il polinomio resto abbia grado minore del grado del polinomio divisore):  x+2 diviso per x fa 1 con resto 2 (infatti x·1+2 = x+2);  d'altronde (x+2)/x = x/x+2/x = 1+2/x;   invece il rapporto tra  x+y  ed  x,  (x+y)/x,  che posso trasformare in  1+y/x,  non posso pensarlo come una divisione con risultato 1 e resto y in quanto  y ha lo stesso grado del divisore, x;  non posso in alcun modo pensare a x+y come  Q(x,y)·x+R(x,y)  con R(x,y) di grado inferiore a quello di x.

Altro

Esistono il massimo comune divisore e il minimo comune multiplo tra polinomi?

Il massimo comune divisore tra due numeri interi positivi è il massimo numero intero positivo per cui entrambi sono divisibili,  il massimo comune divisore tra due polinomi è un polinomio di massimo grado per cui entrambi sono divisibili  (o, volendo, è il polinomio monico - ossia con coefficiente direttivo 1 - di grado massimo per cui entrambi sono divisibili). Ad esempio  3·x²−6·x−9  [= 3·(x²−2·x−3) = 3·(x+1)·(x−3)]  e  6·x²−6  [= 6·(x²−1) = 6·(x+1)·(x−1)]  sono entrambi divisibili per 3(x+1), ma lo sono anche per x+1, per 2x+2, per x/2+1/2, √3·x+√3, …  Volendo scegliere un rappresentante, si prende il polinomio monico x+1.
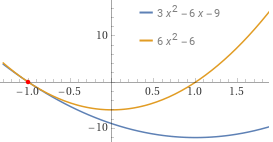I grafici con WolframAlpha:       intersect y = 3*x^2-6*x-9, y = 6*x^2-6

In molti libri di testo si fa fare, invece, anche il m.c.d o il m.c.m. dei coefficienti direttivi! Questo è un tipico esempio di cosa errata: al non farla si risparmia tempo e non si creano danni.

Principio dell'identità dei polinomi: che significa? quando ha senso enunciarlo?

Il teorema di identità dei polinomi afferma che due polinomi sono "formalmente uguali" se e solo se lo sono "funzionalmente", ossia che due funzioni polinomiali di grado n e m  x → a_nxⁿ + a_n–1x^n–1 + …a₂x² + a₁x + a₀  e  x → b_mx^m + b_m–1x^m–1 + …b₂x² + b₁x + b₀ sono uguali se e solo se m=n e per ogni i minore od uguale ad n a_i=b_i.
Nei libri scolastici più diffusi (nel capitolo in cui si studiano le funzioni polinomiali in una variabile) si trova in questa forma:
se due polinomi assumono lo stesso valore per tutti i valori attribuiti alle loro variabili, allora sono identici.
Il principio (al di là della forma che ne danno i libri di testo) è del tutto incomprensibile per gli alunni. Questo è un altro esempio delle cose presenti nei libri di testo da buttare via.
Altra cosa potrebbe essere (in classi molto "buone") affrontare il problema intrecciandosi a riflessioni sui fasci di grafici di funzioni o (estendendosi ai polinomi in 2 indeterminate) a considerazioni legate alle espressioni polinomiali in cos(x) e sin(x):
cos(x)² e 1−sin(x)² sono diverse formalmente ma sono uguali se pensate come funzioni di x (il motivo per cui le cose non funzionano in questo caso è che cos(x) e sin(x) non sono "variabili indipendenti").
Nella "matematica dei matematici" il teorema di identità è importante in quanto non funziona nel caso di alcuni tipi di polinomi. Ad esempio se consideriamo i polinomi che hanno coefficienti nella struttura che i matematici indicano con Z₂, ossia l'insieme {0,1} dotato delle operazioni:
0(+)0=0, 1(+)0=0(+)1=1, 1(+)1=0; 0(·)0=0, 1(·)1=1, 1(·)0=0(·)1=0
  [ossia: m(+)n = (resto della divisone di m+n per 2), m(·)n = ...]
i polinomi x+1 e x³+1 sono diversi mentre le funzioni x → x+1 e x → x³+1 coincidono.
Senza considerazioni di questo tipo, non si capisce il senso di una sua presenza in libri di testo della scuola superiore (l'unica interpretazione benevola è che gli autori le abbiano orecchiate da studenti, senza capirle, e le ripropongano nei libri di testo).