On "polynomials"

In mathematics (as we know from our university studies and from any reliable internet site, for example Wolfram) ...

A function F: x → a_n xⁿ + a_n–1 x^n–1 + …a₂ x² + a₁ x + a₀ with  a_n ≠ 0 is called polynomial function of degree grado n; a_i is called coefficient of degree i.
The coefficients can be constants, variables or more complex terms (as long as they do not contain x).
The equation F(x) = 0 is called polynomial equation of degree n.
The term F(x) is called the polynomial in x of degree n.

The word polygon derives from the Greek words polís (a lot) and gonia (angle), as a "figure with many angles".  Similarly the word polynomial derives from the Greek words polís and ónoma (name, expression), as "expression made up of the sum of many expressions". 
We also speak of trinomial, binomial and monomial to indicate a polynomial which is the sum of 3, 2 or 1 term, that is, in which only 3, 2 or 1 among the a_i are different from 0.

To talk about the degree of a polynomial it is necessary to specify or that it is clear from the context what is the variable to refer to.  For example A+A·B³ can be thought of as a polynomial (in particular, a binomial) of 3rd degree in B, but, transformed into A·(1+B³), it can also be considered a polynomial (in particular, a monomial) of 1st degree in A, or it can be considered as a polynomial of degree 0 in y:  the variable y does not appear in it, therefore as regards y it is a constant.  The variable against which a term is considered a polynomial is sometimes called indeterminate.

In the context of the study of two-input functions, the polynomials in 2 (or more) indeterminates are also considered. E.g. (x,y) → k x³·y² + x·y + y/4 + π is a 2 input polynomial function of degree 5; the degrees are calculated by adding the powers to which the two indeterminates, x and y, are raised.

It should be remembered that the concept of function must not be confused with that of term:  the term x+7 is different from the function A → A+7 !

When and why to study polynomials?

In many textbooks the "polynomials" are studied by developing properties which are instead properties of numbers:  the possibility of reordering a sum or a product, the distributive property, …. And the study of basic functions, essential for the representation of the most common real phenomena (such as x → a+b/x), is postponed.
But, why study polynomial functions?

Because at the end of the 2nd year of high school (after starting the study of the functions in general) some features that distinguish them from the other functions can be brought into focus:

• because between the polynomials in an indeterminate it is possible to define, in analogy with the integers, a division with remainder;
• because the remainder theorem holds;
• because (as a consequence of it) we know that the number of solutions of a polynomial equation does not exceed its degree;
• and because with polynomial functions we can approximate the other functions (and "understand" how it is possible for a computer to calculate sine, exponential, …).

These are only the essential things related to the polynomials on which it makes sense to dwell (at the end of the second year and in the following years).

Note.  The polynomials in 2 or more indeterminates are univocally factorizable  [try to introduce in WolframAlpha for example factor x^3+x^2*y-x^2-x*y:  you get x (x-1) (x + y)x(x-1)(x+y)],  and, therefore, between two of them a maximum common divisor can be found.  [try to introduce in WolframAlpha for example factor x^3+x^2*y-x^2-x*y:  you get x (x-1) (x + y)x(x-1)(x+y)].  But for them we cannot define, in general, a division with remainder  (in which the remainder-polynomial has a degree less than the degree of the divisor-polynomial):  x+2 divided by x is 1 with remainder 2 [(x+2)/x = 1+2/x],  while the ratio between x+y and x, (x+y)/x, which I can transform into 1+y/x, cannot be considered a division with result 1 and remainder y since y has the same degree as the divisor, x.  I can in no way think of x+y as  Q(x,y)·x+R(x,y)  with R(x,y) of a degree lower than that of x

Something else

Are there the greatest common divisor and the least common multiple between polynomials?

The greatest common divisor between two positive integers is the greatest positive integer for which both are divisible;  the greatest common divisor between two polynomials is a polynomial of maximum degree for which both are divisible  (or alternatively it is the monic polynomial - that is, the polynomial with directive coefficient 1 - of maximum degree for which both are divisible). For example  3·x²−6·x−9  [= 3·(x²−2·x−3) = 3·(x+1)·(x−3)]  and  6·x²−6  [= 6·(x²−1) = 6·(x+1)·(x−1)]  are both divisible by 3(x+1), but are also divisible by x+1, by 2x+2, by x/2+1/2, √3·x+√3, …  If we want to choose a representative, we take the monic polynomial x+1.
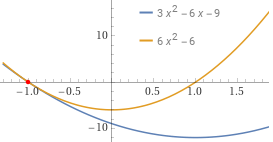The graphs with WolframAlpha:       intersect y = 3*x^2-6*x-9, y = 6*x^2-6

Some textbooks teach pupils to also calculate the g.c.d. and l.c.m. of the highest degree coefficients! This is a typical example of a meaningless thing: not doing it saves time and does not cause damage.

Two polynomials are "formally" equal if and only if they are "functionally" equal. What does it mean? When does it make sense to address this question?

The meaning is this:  two polynomial functions of degrees n and m  x → a_nxⁿ + a_n–1x^n–1 + …a₂x² + a₁x + a₀  and  x → b_mx^m + b_m–1x^m–1 + …b₂x² + b₁x + b₀  are equal if and only if  m=n and for each i less than or equal to n  a_i=b_i.
This property, known as "identity theorem of polynomials", is often found, in Italy and in other countries, in the chapter of school books dedicated to polynomial functions in a variable, generally presented in this form:
if two polynomials assume the same value for all the values attributed to their variables, then they are identical.
The principle (beyond the way it is expressed by textbooks) is completely incomprehensible to pupils. This is another example of the things in textbooks to be thrown away.
Another thing could be (in very "good" classes) addressing the problem by intertwining with reflections on the sheaves of function graphs or (extending to polynomials in 2 indeterminates) with considerations related to the polynomial expressions in cos(x) and sin(x):
cos(x)² and 1−sin(x)² are formally different but are equal if you think of them as functions of x (the reason why things don't work in this case is that cos(x) and sin(x) are not "independent variables").
In "mathematics of mathematicians" the identity theorem is important as it does not work in the case of some types of polynomials. For example if we consider the polynomials that have coefficients in the structure that mathematicians indicate with Z₂, that is the set {0,1} equipped with the operations:
0(+)0=0, 1(+)0=0(+)1=1, 1(+)1=0; 0(·)0=0, 1(·)1=1, 1(·)0=0(·)1=0
  [that is: m(+)n = (remainder of the division of m+n by 2), m(·)n = ...]
the polynomials x+1 and x³+1 are different while the functions x → x+1 and x → x³+1 coincide.
Without considerations of this type, one does not understand the meaning of a presence of this theorem in high school textbooks (the only benevolent interpretation is that the authors have listened to these considerations as students, without understanding them, and propose them again in textbooks).