Indichiamo con T1 e T2 i due termini √(x2+1)-x e 1/(√(x2+1)+x). Alcune possibili uscite: 

  x                    T1                         T2
 1234            0.0004051863193126337     0.00040518631921557805  
 12345           0.00004050222742080223    0.00004050222755607815 
 123456          0.000004050030838698149   0.000004050025920099458 
 1234567         4.048924893140793e-7      4.0500029565014935e-7 
 12345678        4.0978193283081054e-8     4.0500003321000205e-8 
 123456789       0                         4.050000036855001e-9
Gli stessi calcoli fatti con R: 
f1 <- function(x) sqrt(x^2+1)-x
f2 <- function(x) 1/(sqrt(x^2+1)+x)
x <- 12345; c(f1(x),f2(x))
  4.050223e-05  4.050223e-05
x <- 123456; c(f1(x),f2(x))
  4.050031e-06  4.050026e-06
x <- 1234567; c(f1(x),f2(x))
  4.048925e-07  4.050003e-07
x <- 12345678; c(f1(x),f2(x))
  4.097819e-08  4.050000e-08
x <- 123456789; c(f1(x),f2(x))
  0.00e+00  4.05e-09
Man mano che aumento x, moltiplicando circa per 10, per un po' sia T1 che T2 si riducono, dividendosi circa per 10. Del resto, al crescere dell'ordine di grandezza di x il valore di x2+1 tende a coincidere per sempre più cifre significative con quello di x2, e quindi T2 tende a coincidere con 1/(2x), ossia a un termine inversamente proporzionale a x. Il fatto che da un certo punto in poi T1 si scosti da questo comportamento suggerisce che siano intervenuti errori di approssimazione tali da rendere non attendibili i valori visualizzati.
Se rappresentassi graficamente (ad es. con R) l'andamento dei due termini in funzione di x, per valori di x tra due successive potenze di 10, prima o poi assisterei ad un andamento simile al seguente (T2: blu, T1: rosso), il quale confermerebbe che T2 (il termine che "scolasticamente" sarebbe considerato più brutto: molti libri scolastici lo fanno "razionalizzare" in T1), è quello migliore dal punto di vista del calcolo: le strane oscillazioni del grafico di T1 e il suo brutale spiaccicarsi sull'asse x corrispondono all'intervento degli errori di approssimazione. 
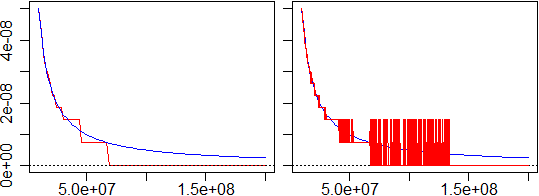
plot(f1,1e7,2e8,col="red")
abline(v=0,h=0,lty=3)
plot(f2,1e7,2e8,add=TRUE,col="blue")
# aumentando i punti
plot(f1,1e7,2e8,add=TRUE,col="red",n=1000)
I problemi per T1 nascono dal fatto che per x con ordine di grandezza grande √(x2+1) e x tendono ad assumere valori sempre più vicini per cui, da un certo punto in poi, interviene il fenomeno della cancellazione delle cifre.

Per altri commenti:   Calcolatore-6

Nota. Anche per studiare l'ordine di infinitesimo di T1 rispetto a 1/x (per x → ∞) è utile trasformarlo nella forma "brutta" T2.