x = 2.1 ± 0.1, y = 2.9 ± 0.1, 1/z = 1/x + 1/y. Quanto vale z?
z = 1 / ( 1/x + 1/y)
1/2.2 ≤ 1/x ≤ 1/2
1/3 ≤ 1/y ≤ 1/2.8
1/2.2 + 1/3 ≤ 1/x + 1/y ≤ 1/2 + 1/2.8
1/(1/2 + 1/2.8) ≤ z = 1 / ( 1/x + 1/y) ≤ 1/(1/2.2 + 1/3)
2 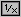
 2.8
2.8 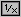

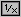 dà 1.1666…
dà 1.1666…
2.2 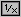
 3
3 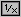

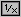 dà 1.26923…
dà 1.26923…
Possiamo considerare 1.166 < z < 1.270 o, com minore accuratezza: z = 1.22 ± 0.05
Usando R potremmo fare:
x <- c(2, 2.2); y <- c(2.8, 3.0)
f <- function(x,y) 1/(1/x+1/y); H <- function(i,j) f(x[i],y[j])
r <- c(H(1,1),H(1,2),H(2,1),H(2,2)); r <- c(min(r),max(r)); r; r[2]-r[1]
# 1.166667 1.269231
# 0.1025641
## Ovvero:
source("http://macosa.dima.unige.it/r.R")
x <- c(2.0,2.2); y <- c(2.8,3.0)
rx <- approssima(1,x, "/")
ry <- approssima(1,y, "/")
rz <- approssima(rx,ry, "+")
z <- approssima(1,rz, "/"); z
[1] min [2] max
[1] 1.166667 1.269231
# o:
approssima2(1,rz, "/")
[1] centro [2] raggio
[1] 1.21794872 0.05128205
Posso più semplicemente impiegare uno script online, avendo
defintito:
function F(x) { with(Math) {
u = 1/(1/x+1/y)
return u
}}

NOTA. Non conviene trasformare z = 1 / ( 1/x + 1/y) in z = x*y / (x+y) per due motivi:
- il calcolo di z mediante una calcolatrice diventa più complesso (x  y
y 
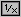
 x
x  y
y  );
);
- trovando intervalli di indeterminazione per x*y e per x+y separatemente si ottiene una precisone peggiore:
x*y sta in [2*2.8, 2.2*3], x+y sta in [2+2.8, 2.2+3]
se u sta in [2*2.8, 2.2*3] e w sta in [2+2.8, 2.2+3], u/w sta in:
[2*2.8/(2.2+3), 2.2*3/(2+2.8)] = [1.07692…, 1.375]
Il motivo di questo peggioramento è che procedendo così non si tiene conto del fatto che u e w non sono indipendenti: se x*y assume valore minimo x+y non può assumere valore massimo.
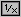
 2.8
2.8 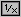

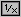 dà 1.1666…
dà 1.1666…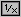
 3
3 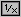

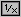 dà 1.26923…
dà 1.26923…
 x
x