Consideriamo l'usuale algoritmo per moltiplicare due matrici.
Vogliamo esaminare come cresce il tempo di calcolo all'aumentare delle
dimensioni delle matrici. Limitiamoci al caso delle matrici quadrate.
Gli altri casi si studiano con piccole varianti.
(1) prova a stimare in base a un ragionamento teorico come, al crescere della dimensione N, cresce il tempo di calcolo t(N),
ossia di valutare l'ordine di infinito di t(N) rispetto a N.
(2) controlla questa stima con uno studio sperimentale mediante un linguaggio di programmazione.
(1)
Calcoliamo A×A con A matrice N×N. Sia B (anch'essa N×N) la matrice prodotto.
Per calcolare B(1,1) eseguo il prodotto scalare della prima riga per la prima colonna:
Per calcolare B(i,j) eseguo il prodotto scalare della riga i per la colonna j:
In ogni caso faccio N moltiplicazioni e N-1 addizioni.
Il tempo è essenzialmente quello per eseguire le operazioni (è trascurabile
quello per gestire il controllo dell'algoritmo: spostarmi da una riga alla successiva, …).
Supponiamo che sia S il tempo per calcolare la somma di due numeri (o, meglio, per trasferire i numeri dalle variabili nei registri
di memoria per gli argomenti, eseguire il calcolo e trasferire il risultato dal suo registro nella variabile di output)
e P quello per calcolarne il prodotto (o, meglio, ...).
Supponiamo che il tempo di calcolo sia sempre lo stesso (ad es. che si tratti di fare sempre calcoli con
numeri arrotondati a 7 cifre).
Per calcolare un prodotto scalare impiego dunque NP+(N-1)S.
I prodotti scalari che devo calcolare sono tanti quanti gli elementi di B, ossia N2.
Quindi t(N) = (NP+(N-1)S)N2 = (P+1)N3-SN2, che ha lo stesso
ordine di N3.
Più precisamente t(N) ≈ (P+1)N3.
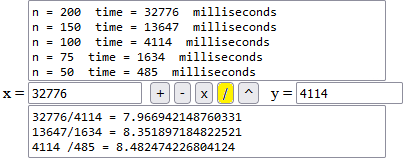
(2) Ecco un possibile programma in JavaScript che genera a caso gli elementi della matrice e valuta il tempo. I possibli esiti:

Al raddoppiare di N t(N) tende a moltiplicarsi per 8 = 23. Posso supporre che che t(N) sia dello stesso ordine di N3.
Per approfondimenti:
 infiniti e infinitesimi neGli Oggetti Matematici.
infiniti e infinitesimi neGli Oggetti Matematici.
Ecco lo studio con R, realizzato con una impostazione simile:
# Metto i dati in una matrice. Suppongo di prendere 240 come dimensione massima
n <- 240; ma <<- matrix(data = runif(n*n), nrow = n, ncol = n)
# La definzione di una funzione t che ad n associa il tempo per calcolare il
# prodotto di due matrici di ordine n
t <- function(n) {
for(i in 1:n) for(j in 1:n) {x <- 0; for(k in 1:n) x <- x+ma[i,k]*ma[k,j]} }
# Faccio un po' di prove, raddoppiando via via n e calcolando il rapporto con
# il tempo precedente
s0 <- 1
n <- 15; s <- proc.time()[3]; t(n); s <- proc.time()[3]-s; s; s/s0; s0 <- s
# 0.03 0.03
n <- 30; s <- proc.time()[3]; t(n); s <- proc.time()[3]-s; s; s/s0; s0 <- s
# 0.19 6.333333
n <- 60; s <- proc.time()[3]; t(n); s <- proc.time()[3]-s; s; s/s0; s0 <- s
# 1.5 7.894737
n <- 120; s <- proc.time()[3]; t(n); s <- proc.time()[3]-s; s; s/s0; s0 <- s
# 12.12 8.08
n <- 240; s <- proc.time()[3]; t(n); s <- proc.time()[3]-s; s; s/s0; s0 <- s
# 95.74 7.89934
# Si vede che raddoppiando n il tempo si moltiplica circa per 8
Disponendo del concetto di derivata, si può effettuare lo studio sperimentale
anche in un altro modo: studiare come varia
# Variazioni del tempo s0 <- 0 n <- 20; s <- proc.time()[3]; t(n); s <- proc.time()[3]-s; s; s-s0; s0 <- s # 0.07 0.07 n <- 40; s <- proc.time()[3]; t(n); s <- proc.time()[3]-s; s; s-s0; s0 <- s # 0.5 0.43 n <- 60; s <- proc.time()[3]; t(n); s <- proc.time()[3]-s; s; s-s0; s0 <- s # 1.75 1.25 n <- 80; s <- proc.time()[3]; t(n); s <- proc.time()[3]-s; s; s-s0; s0 <- s # 4.11 2.36 n <- 100; s <- proc.time()[3]; t(n); s <- proc.time()[3]-s; s; s-s0; s0 <- s # 7.92 3.81 n <- 120; s <- proc.time()[3]; t(n); s <- proc.time()[3]-s; s; s-s0; s0 <- s # 13.07 5.78 # Variazioni delle variazioni: 0.7-0.43; 1.25-0.43; 2.36-1.25; 3.81-2.36; 5.78-3.81 # 0.27 0.82 1.11 1.45 1.97 # Variazioni delle variazioni delle variazioni: 0.82-0.27; 1.11-0.82; 1.45-1.11; 1.97-1.45 # 0.55 0.29 0.34 0.52
Si vede che le variazioni di t(N) crescono. Deduciamo che t(N) è d'ordine superiore rispetto a N (che ha variazioni costanti).
Le variazioni delle variazioni (variazioni seconde) crescono, quindi t(n) è d'ordine superiore rispetto a N2
(che ha derivata seconda costante).
La variazioni terze oscillano attorno a un valore positivo. Questo fa supporre che t(n) abbia l'ordine di N3 (che ha derivata terza costante).