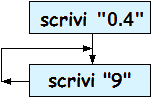
Considera il numero (maggiore di 0.1 e più piccolo di 1) descritto dal diagramma a lato: inzia con "0.4" e poi prosegue con "9", poi "9", e così via, con infinite cifre "9".  Quali tra le seguenti affermazioni su di esso secondo te è corretta?   (A) è inferiore a 1/2,   (B) è maggiore di 1/2,   (C) è eguale a 1/2,   (D) non si può stabilire quali delle altre tre risposte sia giusta

La risposta giusta è la (C). Vediamo perché.  Se traccio il punto 0.49, poi il punto 0.499, poi il punto 0.4999, … procedendo in questo modo, se potessi operare sulla retta dei numeri astratta e con strumenti in grado di tracciare punti "senza spessore", mi avvicinerei sempre più al punto 0.5.  Che distanza da 0.5 ha il punto 0.499? 0.001.  E il punto 0.499999? 0.000001.  E il punto 0.4999… con infinte cifre "9"?  0.
È impossibile distinguere il punto 0.4999… dal punto 0.5, il punto 0.999… dal punto 1. Analogamente è impossibile distinguere, ad esempio, 67.2999… dal punto 67.3. Sono espressioni diverse dello stesso numero.
Nel caso del quesito, 0.4999… è eguale a 0.5000…, ovvero a 1/2.

Del resto 0.777… = 7/9, 0.111… = 1/9, 0.555… = 5/9 e  0.999… = 9/9 = 1

Il fatto che i numeri decimali finiti posso rappresentarli sia con periodo "9" che con periodo "0" è importante anche per interpretare le uscite "strane" che a volte si ottengono con alcune calcolatrici tascabili (1/3*3 in alcune CT dà 0.999…). Analogamente in base 2 l'espressione 0.111… rappresenta il numero 1 (1/2 + 1/4 + 1/8 + 1/6 + … = 1).  A destra è raffigurato come questa idea si ritrovi molte volte, anche nelle situazioni più elementari:  con quale probabilità, lanciando una moneta equa, testa mi viena al 1° lancio, e al 2°, e al 3°, …

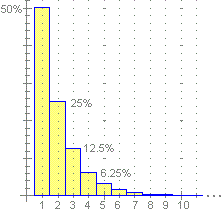L'area dell'istogramma a sinistra è un esempio di figura illimitata (la base dell'istogramma prosegue senza fine a destra) con area finita, uguale a 1.

Per approfondimenti vedi I numeri negli Oggetti Matematici