solve x^2 = 2 using bisection method for 0 <= x <= 2 with 1 digits precision
solve x^2 = 2 using bisection method for 0 <= x <= 2 with 2 digits precision
...
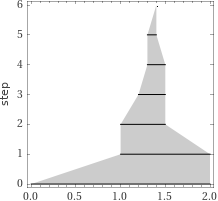
Se definisco √2 come il numero il cui quadrato è 2, come spiego agli alunni che un tale numero esiste?
La spiegazione è semplice, se accoppiata al modo in cui calcolare √2. Nei libri di testo invece in genere o si prende implicitamente per buono che esista un numero che al quadrato faccia 2 o lo si spiega con buffe (e quasi sempre errate) costruzioni dei numeri reali a partire dai razionali.
Indichiamo x0, x1, x2,
… le approssimazioni per difetto a meno di 0.1, 0.01, 0.001, … di un eventuale numero il cui quadrato sia 2,
ovvero sia:
Il procedimento precedente mi garantisce anche che il quadrato del numero così generato è proprio 2. Infatti il prodotto di due numeri illimitato lo si fa operando sulle sue approssimazioni per difetto e per eccesso, e quanto fatto mi permette di concludere che elevando al quadrato, ossia moltiplicando per sé stesse, le approssimazioni per difetto e per eccesso del numero così trovato a potenze di 10 man mano più piccole ottengo valori che si stringono sempre più attorno a 2.
La spiegazione, opportunamente semplificata, è affrontabile anche nella scuola media inferiore. Vedi ad esempio QUI la spiegazione legata all'uso di una calcolatrice.
Per altri commenti vedi qui
Qui un algortimo per calcolare, passo per passo, la radice quadrata di un numero. Prova a calcolare √2.
|
Qui, negli "esempi", come procedere usando WolframAlpha:
solve x^2 = 2 using bisection method for 0 <= x <= 2 with 1 digits precision |  |