Il 2º volume di un diffuso libro di matematica per le superiori esemplifica alcune attività sui radicali con questo esempio:

Applicando la definizione, stabilire per quali valori di x il seguente radicale è definito:

5√ x2(x+1)
—————
(1+x2)(x+3)

Un radicale aritmetico deve avere radicando non negativo. È necessario pertanto che la frazione che rappresenta il radicando sia maggiore o eguale a zero. Studiamo dunque la disequazione frazionaria:

x2(x+1) ≥ 0
—————
(1+x2)(x+3)

       -3      -1
N1  +       +       +
N2  -       -   0   +
D1  +       +       +
D2  -   x   +       +
——————————————————————    
    +   x   -   0   +
Il radicando è non negativo se x < − 3 o x ≥ −1. Questi sono i valori di x per i quali il radicale è definito.

Come valuti questo approccio ai radicali (e l'impostazione del libro)?

Ecco come farebbe l'esercizio una persona che conosce un po' di matematica.
La radice quinta, cosė come qualunque radice di ordine dispari, è definta ovunque.  Il termine dato è quindi definito dove è definito il radicando . Quest'ultimo non è definito solo dove si azzera il secondo termine della divisione, il quale si annulla quando x = −3.
In definitiva il termine dato è definito in (−∞,−3) ∪ (−3,∞).

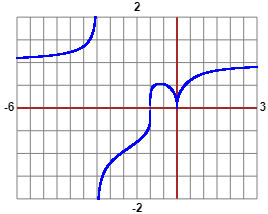
Sotto, per curiosità, la conferma tracciando il grafico in funzione di x:

Vedi qui.

Alcune osservazioni sulla soluzione proposta dal libro.

(1)  In questo libro si parla di radicali aritmetici.  È uno strano concetto presente anche in altri libri di testo italiani, ma che ha poco a che fare col concetto che, un tempo, si usava individuare con tale termine, per distinguerlo dai radicali algebrici:  col primo si indicava quella che oggi viene chiamata semplicemente "radice", col secondo si indicava l'insieme delle soluzioni di un'equazione (con incognita x) del tipo xn = k;  ad es. nel caso di x2=4 si avrebbe {−2,2}.  In questi libri viene chiamato radicale aritmetico la radice solo dei numeri non negativi.  Quindi 3√(-8) (che sappiamo essere -2) non esisterebbe.  Poi, quando si passerebbe a quelli che secondo gli autori sarebbero i radicali algebrici, si potrebbe, magicamente, riprendere in uso tale termine!  Vediamo anche che cosa si trova in WikiPedia (versione inglese, che conviene sempre usare piuttosto che quella italiana!), QUI.

(2)  Poi per stabilire il segno del radicando vengono proposte la costruzione e l'uso meccanico della tabellina dei segni invece che procedere nel modo "ragionato", e molto "semplice", come quello proposto nella soluzione presentata.  L'obiettivo, implicito, del procedimento illustrato del libro č l'educazione ad usare metodi meccanici piuttosto che forme elementari di argomentazione.

Osserviamo che lo stesso libro, come molti altri, propone anche, in modo analogo, un uso meccancio della cosiddetta regola di Ruffini.  Essa non è da non confondere con l'importante "teorema di Ruffini" (vedi):  è un procedimento "magico", che oscura il significato della divisione tra polinomi, di cui è facile perdere il controllo semantico, che funziona solo in alcuni casi di divisione, e che non fa risparmiare un gran ché né in termini di spazio né in termini di tempo.  Data la sua natura didatticamente dannosa,  riportiamo qui  le considerazioni su di essa svolte da Vinicio Villani in un capitolo di un suo bellissimo libro (che ogni insegnante dovrebbe leggere).  [nota:  all'estero è nota in genere come "regola di Horner"  (vedi: http://en.wikipedia.org/wiki/Horner's_method); Horner e Ruffini hanno messo a punto questo metodo entrambi intorno al 1810, anche se esso era già stato individuato più di 500 anni prima dal cinese Chu Shih-Chieh;  la "regola" ha alcune applicazioni specifiche che danno ad essa un ruolo ben diverso da quello esercitato dalle pratiche didattiche;  all'estero in genere non c'è alcuna traccia di questa regola nei libri di testo;  vedi qui quanto è dedicato alla divisione tra polinomi nell'eserciziario di algebra che per decenni è stato il più diffuso al mondo]