x ≅ -0.324783298321785
x ≅ 0.324680429277547
x ≅ 8696.00010286904
Un insegnante decide di proporre agli studenti (in una classe seconda di scuola superiore) la risoluzione dell'equazione:
x³ − 8696·x² − x + 917 = 0
L'idea è quella di far loro usare del software per ricercare le soluzioni con metodi grafici e/o numerici (comprensibili),
senza l'impiego di WolframAlpha che la risolverebbe automaticamente. Secondo te, quali problemi vorrebbe far emergere e/o quali
questioni vorrebbe affrontare/sistemare l'insegnante con questa attività?
Vediamo, innanzi tutto, a livello adulto, come si potrebbero trovare le soluzioni.
(1) Un primo modo è quello che tiene conto che si tratta di una equazione polinomiale. Potremmo usare
uno dei molti software che cosentono di risolvere equazioni di questo tipo.
Vediamo che cosa si può ottenere con R (vedi QUI il punto K3):
# source("http://macosa.dima.unige.it/r.R") # <- mettilo se non lo hai già caricato
# Uso il comando solpol( c(a0,...,aN) ) per risolvere a0 + a1*x +...+ aN*x^N = 0
solpol( c(917, -1, -8696, 1) )
# 0.32468042927755
# -0.32478329832179
# 8696.000102869
Usando WolframAlpha otterrei:
x^3-8696*x^2-x+917 = 0
x ≅ -0.324783298321785
x ≅ 0.324680429277547
x ≅ 8696.00010286904
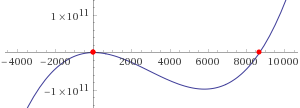
(2a) In alternativa, potrei trovare le soluzioni combinando l'utilizzo di un programma per tracciare i grafici e quello di
un algoritmo per la ricerca delle soluzioni delle equazioni (nei casi in cui in esse cambi segno il polinomio).
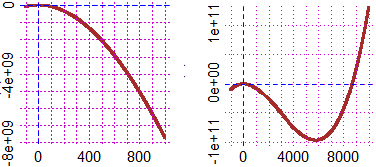
Per il grafico possiamo ricorrere a questo script , avendo definito
function f(x) { y = Math.pow(x,3)-8696*Math.pow(x,2)-x+917 ; return y }
aX = -3000; bX = 10000; aY = -1e11; bY = 1e11
Dx = 1000; Dy = 1e10
e poi
aX = -100; bX = 100; aY = -1e8; bY = 1e7
Dx = 10; Dy = 1e7
...
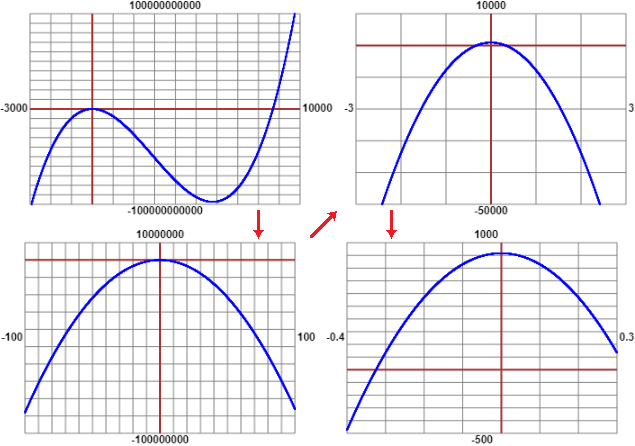
Per il calcolo usiamo questo semplice script.
Con un "test" individuo gli intervalli dove la funzione cambia segno e poi attraverso dei successivi dimezzamenti trovo (con la precisione che voglio, ma tenendo conto che le cifre
non sono tutte buone: mi conviene arrotondare a 8 cifre - siamo in un tratto quasi orizzontale) le soluzioni. Trovo 8696.0001, 0 .32111953, -0 .32122267.
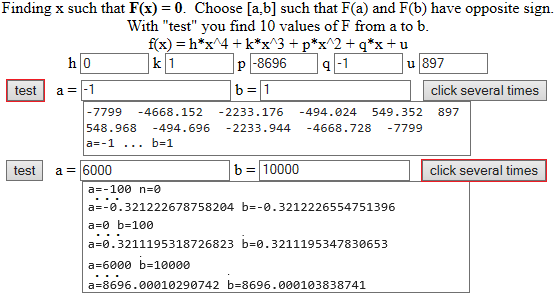
(2b) Potrei usare del software che mi consenta sia di trovare le soluzioni combinando il tracciamento dei grafici e l'impiego di
un algortimo per la ricerca delle soluzioni delle equazioni (nei casi in cui in esse cambi segno il polinomio) sia di impiegare un algortimo per la ricerca dei massimi
e dei minimi di una funzione (nei casi in cui gli zeri dei polinomi siano in punti di massimo o minimo relativi). Ecco ad esempio come impiegare
R (vedi QUI il punto K_3). So che l'equazione è polinomiale di 3º grado e
che ha coefficiente direttivo positivo (è 1): siamo di fronte ad una funzione che per x → ∞ tende a ∞ e che
per x →
f = function(x) x^3-8696*x^2-x+917
graphF( f, -100,100, "brown")
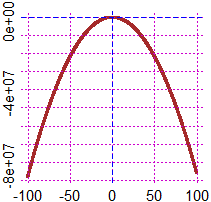# allargo a destra, dove deve scavalcare l'asse orizzontale e andare a ∞
graphF( f, -100,1000, "brown")
graphF( f, -1000,10000, "brown")
# cerco la soluzione a destra, anche con più cifre
soluz( f,0, 8e3, 10e3); more(soluz( f,0, 8e3, 10e3))
# 8696 8696.00010286904
# cerco di capire che cosa accade a sinistra
graphF( f, -10,10, "brown")
graphF( f, -1,1, "brown")
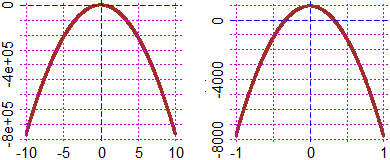# capisco che i punto di max ha ordinata positiva; ci sono 2 soluz.
more(soluz( f,0, 0, -1) ); more(soluz( f,0, 0, 1) )
# -0.324783298321785 0.324680429277547
# Ovviamente potrei trovare le soluzioni anche con successivi zoom grafici,
# arrivando ad es. a:
 |
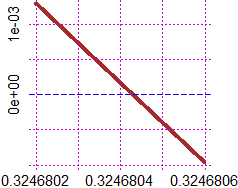0.3246804 |
Quali potrebbero essere gli obiettivi di chi propone questo problema − da affrontare con gli strumenti descritti in (2) − agli alunni di una classe seconda di una scuola superiore?
• far riflettere gli alunni, mettendoli in crisi, sul fatto che senza qualche ragionamento il solo uso del computer non consente di trovare
con certezza tutte le soluzioni: anche facendoli lavorare a gruppi probabilmente vengono individuate solo le due soluzioni tra −1 ed 1;
• avviare considerazioni sulle equazioni polinomiali, che conducano alla messa a fuoco del teorema del resto e della
sua conseguenza che una equazione polinomiale in una incognita ha al più tante soluzioni quanto è il suo grado;
• mettere a fuoco il fatto che l'uso, "ragionato", del computer consente, anche a un ragazzo di seconda superiore, di trovare
le soluzioni di una equazione del tipo
• e, eventualmente, accennare agli alunni che solo per alcune classi di equazioni esistono delle
formule risolutive (anche per quelle polinomiali, anche se con tecniche di cui gli alunni non dispongono).