Risolvi rispetto a x la disequazione 8^x+1 ≥ 2^x2.

Il termine 2^x2 in genere [ struttura dei termini] è interpretato come 2^(x2)

Posso procedere in vari modi. Ad es. se osservo che 8 = 2³ posso riscrivere la disequazione così
2^3(x+1) ≥ 2^(x2)   che, essendo x 2^x crescente, equivale a:
3x+3 ≥ x²
Potevo ottenere lo stesso risultato applicando la funzione logaritmo, anch'essa crescente:

log2(8x+1) ≥ log2(2(x2))   (x+1)log2(8) ≥ x2 log2(2)   3x+3 ≥ x2 Le soluzioni (vedi figura a lato) sono i valori dell'intervallo che ha per estremi le ascisse dei punti di intersezione di y = 3x+3 e y = x2 Risolvo: x2 - 3x - 3 = 0 (x - 3/2)2 - 9/4 -3 = 0 x = 3/2 ± √(3+9/4) = 3/2 ± √21 / 2 Le soluzioni della disequazione sono gli elementi dell'insieme [(3-√21)/2, (3+√21)/2].

Infine potevo ragionare direttamente sui grafici di y = 8^x+1 e di y = 2^(x2), stabilire che le soluzioni della disequazione sono i valori dell'intervallo che ha per estremi le ascisse dei punti di intersezione di questi, e determinare tale intersezioni risolvendo:
8^x+1 = 2^(x2).

Posso controllare la soluzione di x² - 3x - 3 = 0 con uno script:

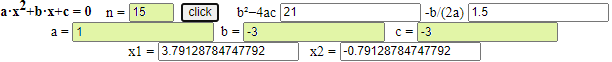
Possiamo controllare la risposta con WolframAlpha:
solve 8 ^ (x+1) >= 2 ^ (x^2)       →   1/2 (3 - sqrt(21)) <= x <= 1/2 (3 + sqrt(21))