
Risolvi rispetto a x la disequazione sin(x) < cos(2x)
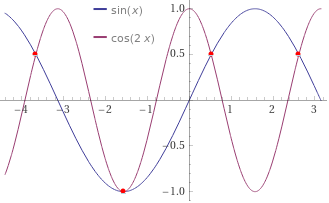
| sin(x) < cos(2x) è vera per i valori delle ascisse per le quali la curva y=sin(x) sta sotto alla curva y=cos(2x). Tenendo conto che la seconda è una sinusoide contratta orizzontalmente, possiamo concludere che nelle vicinanze dei punti di ordinata 1 in cui le due curve si toccano (sono gli x tali che sin(x)=-1, ossia del tipo -π/2+2kπ con k intero) y=sin(x) sta sotto ad essa, e (trattandosi di funzioni continue) rimane sotto fino al successivo (verso destra o verso sinistra) punto di intersezione. |  |
Abbiamo così concluso che la disequazione è vera in un intervallo del tipo (-π/2-h, -π/2+h) privato del centro, ossia (-π/2-h,-π/2) U (-π/2,-π/2+h), e negli insiemi ottenuti da questo con traslazioni di multipli di 2π.
Per trovare esattamente le intersezioni (ci basta trovare il "?") dobbiamo fare qualche manipolazione. Ci è utile utilizzare
sin(x) = cos(2x) <==> sin(x) = cos(x)2-sin(x)2 <==> sin(x) = 1-2 sin(x)2 <==>
u2 + u/2 – 1/2 = 0 <==> (u+1/4)2-1/16-1/2 = 0
<==> (u+1/4)2 = 9/16
<==>
[ovviamente potevo risolvere 2u2+u–1 = 0 rispetto a u direttamente]
Dunque "?" corrisponde a quando u = sin(x) = 1/2, ossia a x = 30° = π/6. Il simmetrico rispetto a -π/2 è -π-π/6 =
-7π/6.
Concludendo la disequazione è vera per x in
I grafici fatti con questo script.

Posso controllare le soluzioni con WolframAlpha:
solve for x sin(x) = cos(2*x)
x = 1/2 π (4 n - 1) and n element of Z
x = π (2 n + 1/6) and n element of Z
x = π (2 n + 5/6) and n element of Z
Fatto il grafico, posso trovare le risposte anche utilizzando questo script online per trovare la soluzione di un'equazione e questo per trovare il minimo di una funzione, avendo definito "F" nel modo seguente:
function F(x) {
with(Math) {
y = cos(2*x)-sin(x)
return y
}}
primo script test: a=-2 ... b=8 0.25565380596 0.42532414826 1 -1.25761782136 -1.56294104769 0.81905027859 0.6113024615 0.11985274559 1.12326945693 -0.52024938051 -1.94701772695 click: a=-1 ... b=1 ... a=0.5235987755982988 b=0.5235987755982989 click: a=2 ... b=3 ... a=2.617993877991494 b=2.6179938779914944 secondo script a=4 ... b=6 ... a=4.712388882507636 ... b=4.712389056344137 0 0 0 0 0 0 0 0 0 0 0 SOLUZIONI 0.523598775598299 2.617993877991494 4.712389
Per altri commenti:
 funz. circolari e trigonometria
neGli Oggetti Matematici.
funz. circolari e trigonometria
neGli Oggetti Matematici.
# Con R
source("http://macosa.dima.unige.it/r.R")
f <- function(x) sin(x); g <- function(x) cos(2*x)
graficoF( f, -2*pi,3*pi, "blue"); grafico( g, -2*pi,3*pi, "red")
for(i in 1:5) diseq(g,f, -2*pi,3*pi, "brown")
soluz2(f,g, 0,2)
# 0.5235988
frazio(soluz2(f,g, 0,2)/pi)
# 1/6 tra 0 e 2 l'intersezione è in pi/6
frazio(soluz2(f,g, 2,4)/pi)
# 5/6 tra 2 e 4 l'intersezione è in 5/6*pi
