

 |
Considera l'equazione differenziale y'(x)=(x+y)/(x-y). A sinistra ne è tracciato il campo direzionale, col software online WolframAlpha, destra con R (vedi), assieme alle curve che ne rappresentano le soluzioni passanti per alcuni punti particolari; quella passante per (3,1) è in realtà una "curva integrale", non il grafico di una funzione: è ottenuta raccordando i grafici di alcune soluzioni in modo da ottenere una curva "liscia". Prova, usando uno dei due sofware, a tracciare il campo direzionale e i grafici di alcune soluzioni. Secondo te, in questo caso, fissato un punto P diverso dall'origine, esiste un'unica curva integrale passante per esso? |  |
Il campo direzionale in WolframAlpha è stato tracciato con
1/2 log(y(x)^2/x^2 + 1) - tan^(-1)(y(x)/x) = c_1 - log(x)
che capisco essere parziale: log(x) non è definito per x non positivo.
Infatti se traccio i grafici per diversi valori dalla costante c_1 ottengo:
plot log(y^2/x^2+1)/2-atan(y/x)=0-log(x), log(y^2/x^2+1)/2-atan(y/x)=1-log(x), log(y^2/x^2+1)/2-atan(y/x)=-1-log(x), -3<x<3,-3<y<3
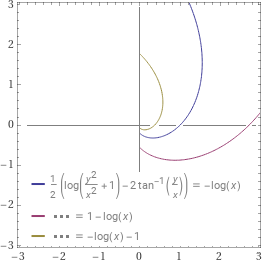
Questo esempio mostra l'importanza di tracciare il campo direzionale per interpretare o correggere le soluzioni ottenute (con del software o a mano).
In questo caso, come risulta evidente dal campo direzionale, per ogni punto diverso da (0,0), passa una sola curva integrale. Tutte le curve integrali, che hanno una forma di spirale (vedi la figura seguente, e il seguito del documento se sei interessato a come ne è stata ottenuta l'equazione) tendono a convergere nell'origine degli assi.

Per altri commenti:  Modelli differenziali.
Modelli differenziali.
Con R.


La figura precedente a destra è uno zoom di quella a sinistra. Ecco, sotto, come potrebbe essere usato il programma per tracciare il campo direzionale, tre soluzioni e una "curva integrale".
Dy = function(x,y) (x+y)/(x-y) BF=4; HF=4; PLANE(-3,3, -3,3) diredif(-3,3, -3,3, 20,20) # il campo direzionale # soledif(-2,1, -3, 1e5, "red") # ramo sinistro per -2,1 soledifvc(-2,1, 1, 1e6) # -1.146134 1.146135 -1.146131 1.146135 punto di max # 0.23827 0.2309335 0.238273 0.2311254 dove deve finire il grafico # 0.238333 0.2394669 0.238336 0.2382028 # 0.238336 0.2382028 0.238339 0.2489395 soledif(-2,1, 0.2384, 1e5, "red") # ramo destro per -2,1 # soledif(0,-2, 3, 1e5, "red") # ramo destro per 0,-2 soledifvc(0,-2, -1, 1e6) # -0.644798 -0.6428732 -0.644799 -0.6435422 dove deve finire il grafico # -0.644801 -0.6501102 -0.644802 -0.6498663 # -0.644814 -0.6292961 -0.644815 -0.6293782 # -0.644911 -0.64579 -0.644912 -0.6443215 soledif(0,-2, -0.6447, 1e5, "red") # ramo sinistro per 0,-2 # soledif(2,-1, 3, 1e5, "red") # ramo destro per 2,-1 soledifvc(2,-1, -1, 1e6) # 1.146134 -1.146135 1.146131 -1.146135 punto di min # -0.23827 -0.2309335 -0.238273 -0.2311254 dove deve finire il grafico # -0.238333 -0.2394669 -0.238336 -0.2382028 # -0.238336 -0.2382028 -0.238339 -0.2489395 soledif(2,-1, -0.2382, 1e5, "red") # ramo sinstro per 2,-1 soledif(3,1, 3.5, 1e5, "brown") soledifvc(3,1, -1, 1e6) # 0.73902 -0.739022 0.739016 -0.739022 # -0.15364 -0.1533294 -0.153644 -0.1572831 # -0.153644 -0.1572831 -0.153648 -0.1569414 # -0.153672 -0.1512396 -0.153676 -0.151741 soledif(3,1, -0.15364, 1e5, "brown") # # In x=-0.15364 la tangente è verticale. Proseguendo otteniamo la "curva integrale": soledifvc(-0.1536,-0.1534, 1, 1e6) # -0.03193212 0.03193244 -0.03193096 0.03193244 # 0.006641962 0.005883512 0.006643115 0.005902564 # 0.006667341 0.006743753 0.006668494 0.006541285 # 0.006668494 0.006541285 0.006669648 0.006661078 soledif(-0.1536,-0.1534, 0.00664, 1e5, "seagreen") soledifvc(0.00664,0.00589, -1, 1e6) # 0.001385339 -0.001385752 0.001384333 -0.001385752 # -0.0002907164 -0.0001157092 -0.000291723 -0.0001180469 # -0.0003350086 -0.0006045393 -0.0003360152 -0.0006010303 # -0.0003712476 -0.0003545058 -0.0003722542 -0.0003981435 soledif(0.00664,0.00589, -0.000335, 1e6, "seagreen") # Ci fermiamo, in quanto il seguito della "spirale" non si distinguerebbe.
Lo "zoom":
BF=3; HF=3; PLANE(-0.16,0.05, -0.16,0.05) soledif(3,1, -0.1536, 1e6, "brown") soledif(-0.1536,-0.1534, 0.00664, 1e5, "seagreen") soledif(0.00664,0.00589, -0.000335, 1e6, "seagreen")
La descrizione analitica della curva integrale:
R = function(a) k*exp(a); k = sqrt(10)/exp(atan(1/3)); k # 2.292269 # La curva realizzata in forma polare si sovrappone a quella tracciata sopra: pola(R, -30,0, "blue") # Vediamo anche qualche zoom: BF=2.5; HF=2.5 b=1e-1; PLANE(-b,b, -b,b); pola(R, -30,0, "blue") b=1e-2; PLANE(-b,b, -b,b); pola(R, -30,0, "blue") b=1e-3; PLANE(-b,b, -b,b); pola(R, -30,0, "blue") b=1e-5; PLANE(-b,b, -b,b); pola(R, -30,0, "blue") b=1e-4; PLANE(-b,b, -b,b); pola(R, -30,0, "blue")