Risolvi (rispetto all'unica variabile, x) l'equazione
  (2x-1)·(2x+1)·(3x+1) = 0

(2x-1)(2x+1)(3x+1) = 0 quando almeno uno tra 2x-1, 2x+1 e 3x+1 vale 0. Quindi vi sono tre possibilità affinché l'equazione sia vera:
2x-1 = 0, ossia 2x = 1, ossia x = 1/2;
2x+1 = 0, ossia 2x = -1, ossia x = -1/2;
3x+1 = 0, ossia 3x = -1, ossia x = -1/3.
  Queste sono le tre soluzioni.

    Il quesito sembra molto facile, tuttavia in un test di ingresso somministrato a un grande campione (7300 persone) delle matricole delle facoltà scientifiche delle Università di Genova e di Pisa (nel 1982 e nel 1983) vi sono state solo il 64% di risposte esatte, e non sempre ottenute nel semplice modo illustrato sopra.
    Moltissimi studenti hanno moltiplicato i tre polinomi ottenendo una equazione polinomiale di 3° grado che poi si sono messi a cercar di risolvere con tecniche varie di scomposizione o di fronte alla quale hanno affermato di non conoscere la formula risolutiva delle equazioni di 3° grado.
    Vi è la cattiva abitudine (forse coltivata dall'insegnamento) di affrontare tutto con delle manipolazioni o cercando di ricordare qualche "ricetta", invece di cercare di analizzare in modo più riflessivo i problemi proposti (e, in questo caso, pensare al significato di "soluzione di una equazione").

    Analogamente, di fronte allo studio della curva y = 3(x−2)² + 4  è controproducente passare alla esplicitazione nella forma polinomiale standard del secondo termine, ma molti alunni procedono così, in modo da usare il loro bagaglio di formulette per le equazioni di 2º grado, come sono stati abituati a fare.

    È opportuno, comunque, far osservare agli alunni che mentre lo "sviluppo" del prodotto è controproducente nei casi come questo, in cui esso viene eguagliato a 0, non è detto che lo sia nel caso di altre equazioni, come  (2x-1)(2x+1)(3x+1)=x+1  o  (2x-1)(2x+1)(3x+1)=(3x²+5)(4x+3).  Vedi sotto.

Risoluzione (rispetto ad x) di (2x-1)(2x+1)(3x+1) = x+1.
Posso manipolare (2x-1)(2x+1)(3x+1)-(x+1).

Posso procedere facilmente a mano, ma vediamo come farlo con del software, ad esempio con questo script:

(2x-1)(2x+1) → 4x²-1,  (4x²-1)(3x+1) → (12x³+4x²-3x-1),  (12x³+4x²-3x-1)-(x+1) → 12x³+4x²-4x-2

Posso rappresentare graficamente x → 12x³+4x²-4x-2 con questo script:

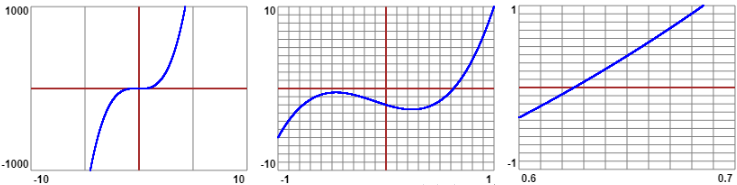
Capisco che la soluzione è circa 0.625.  La trovo con precisione con un altro script:

Cliccando ripetutamente arrivo a:  a = 0.6255181996522395,  b=0.6255181996522396

Se voglio trovare la soluzione esatta posso introdurre 0.6255181996522395 o 0.6255181996522396 in WolframAlpha ottenendo:

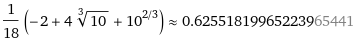
Volendo, in WolframAlpha potevo introdurre direttamente  (2*x-1)*(2*x+1)*(3*x+1) = x+1  ottenendo lo stesso risultato.

Risoluzione (rispetto ad x) di (2x-1)(2x+1)(3x+1) = (3x²+5)(4x+3).
Posso manipolare, come sopra, (2x-1)(2x+1)(3x+1)-(3x²+5)(4x+3).

(2x-1)(2x+1)(3x+1) → (12x³+4x²-3x-1),  (3x²+5)(4x+3) → 12x³+9x²+20x+15

(2x-1)(2x+1)(3x+1)-(3x²+5)(4x+3) → -5x²-23x-16.
Parabola con la concavità verso il basso.
Le soluzioni dell'equazione (usando questo script):

Ovvero  (-23+√209)/10  e  (-23-√209)/10