Risolvi, usando del software, graficamente e numericamente, la seguente disequazione. Prova, quindi, a risolverla "esattamente".
|x² + 3·x| + x² − 2 ≥ 0
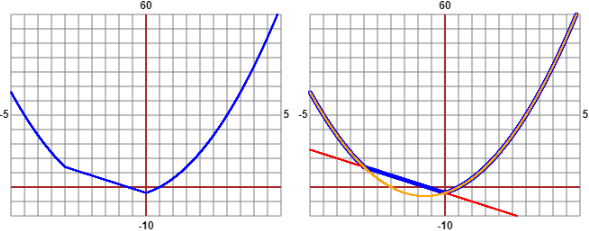
Se provo a tracciare il grafico di y = |x² + 3·x| + x² − 2 ottengo la rappresentazione sotto a sinistra. Capisco immediatamente che si tratta di una parabola "tagliata", come si vede nel grafico a destra.
Se distinguo i casi in modo da togliere il valore assoluto ottengo le due curve: |  |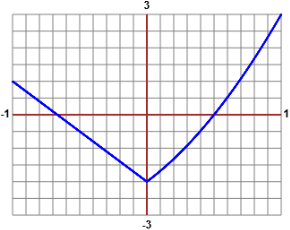
Quindi la curva non sta sotto all'asse x per x ≤ A e x ≥ B dove A e B sono le ascisse del punto in cui la retta taglia l'asse x e del punto destro in cui lo taglia la parabola. Posso trovare facilmente questi punti risolvendo a mano due semplici equazioni. Vediamo come potremmo farlo con del software:
Quindi la soluzione della disequazione è: x ≤ -0.666… = -2/3 OR x ≥ 0.5.
I grafici sono stati tracciati usando questo script. Le equazioni sono state risolte usando questo script.
Posso controllare rapidamente la risposta con WolframAlpha:
|x^2 + 3*x| + x^2 - 2 >= 0
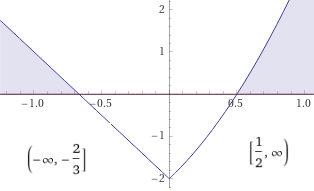
Come avrei potuto utilizzare R:
source("http://macosa.dima.unige.it/r.R")
f = function(x) abs(x^2+3*x) + x^2 - 2
graficoF(f, -5,5, "brown")
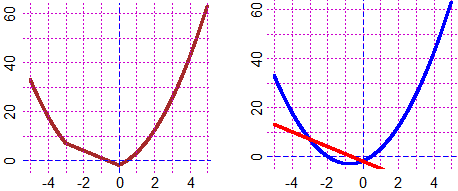# Che il grafico sia quello sopra a sinistra potevo dedurrlo dal fatto che f(x) è
# 2x^2+3x-2 o -3x-2:
g = function(x) 2x^2+3x-2; h(x) = function(x) -3x-2
grafico(g, -5,5, "blue"); grafico(h, -5,5, "red")
# faccio uno zoom (ottengo il grafico seguente):
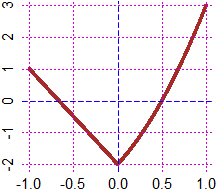graficoF(f, -1,1, "brown")
soluz(f,0, -1,0) # [1] -0.6666667
soluz(f,0, 0,1) # [1] 0.5
# Posso trovare "manualmente" le soluzioni.
# La soluzione a sinistra è l'intersezione della retta con l'asse x:
# y = -3x-2 vale 0 per 3x = 2, ossia x = -2/3 = -0.666…
# La soluzione a destra è l'intersezione destra della parabola con l'asse x:
# 2x^2+3x-2 = 0 quando x=-2 o x=1/2; a noi interessa x = 1/2.